What if Charles Darwin Built a Neural Network?

Author(s): Alexander Kovalenko

Originally published on Towards AI.

An alternative way to “train” a neural network with evolution

At the moment, backpropagation is nearly the only way for neural network training. It computes the gradient of the loss function with respect to the weights of the network and consequently updates the weights by backpropagating the error across the network layers using the chain rule.

Recently, the community has been trying to go beyond backpropagation, as maestro Geoffrey Hinton himself, who popularized the algorithm in the '80s, is now “deeply suspicious” about it. His view now is “throw it all away and start again”. There are many reasons behind his suspicion. The main one is that our brain does not backpropagate things, as there is no labeled data. We rather label things by ourselves, which this is a completely different story. Many brilliant works have been published at NeurIPS featuring diverse algorithms, some of which are rather sophisticated. However, we are here not for some hardcore algorithm that looks like an ancient spell to summon the devil but for something simpler. Much simpler. Instead of training our model, we are going to evolve it, just like mother nature did.

Now, it is time for Charles Darwin to come into the picture. Darwin defined evolution as “descent with modification”. Sounds almost like “gradient descent”, right? 😅 Natural selection, which is a key point of evolution, means that species evolve over time, give rise to new species, and share a common ancestor. In simple words, the most adapted fraction of the population survives and produces the slightly altered (i.e., mutated) offspring. Then, this process repeats over and over for a long time… How long? For example, in the case of the planet Earth, it took 4.543 billion years. This concept is well-adapted in computer science and is called a genetic or evolutionary algorithm.

Given a large population, starting at random, evolution can emerge with surprisingly good results. Likewise, “The infinite monkey theorem”, states that a monkey, given an infinite amount of time, will almost surely type some meaningful text, say, William Shakespeare’s Hamlet.

“Let us suppose that a million monkeys have been trained to type at random, and that these typing monkeys work hard for ten hours a day with a million typewriters of various types. After a year, results of their work would contain exact copies of the books of all kinds and languages held in the richest libraries of the world”

Émile Borel, 1913, Journal de Physique

How do we extrapolate this idea to neural network training? Just imagine that we started with a bunch of random nets. They can vary in terms of architecture, weight, or any other parameters. Then we have to check how they do the job, choose a small chunk that performs the best, and do some small modifications (which is called “mutation”) to their parameters. Since we are talking about backpropagation alternatives, here, the goal will be to find the best weights and biases for the neural network without a “traditional” way to train it.

No backpropagation, no gradient descent – no problems!

First, let’s make our lives easier by creating a neural net utilizing the PyTorch library. For simplicity, we’ll take a feed-forward neural network with a single hidden layer and evolve it for a simple task – handwritten digits recognition, which we all know as the MNIST dataset:

Now, to make the model work, we have to initialize weights and biases, thus let’s create a function that takes a model and trainable parameters and puts them all together:

Then, we need the so-called fitness function, which according to good old Wikipedia, is:

a particular type of objective function that is used to summarise, as a single figure of merit, how close a given design solution is to achieving the set aims.

At first, let’s use the standard PyTorch test function without mini-batches, as we don’t need them anymore:

Therefore, it is the so-called fitness function that we have to maximize. As it returns the accuracy, maximizing fitness function sounds like a plan!

To test the model, we, however, need some input which would be a population of random neural network parameters. Therefore, first, we need to create the population by simply generating many pseudorandom normally distributed tensors of a certain shape, with a little normalization tweak meant to avoid very large parameters, which is simply multiplying the weights and biases by 0.1.

Let’s do it as a list of Python tuples:

Here, every tuple contains the following:

• weights of the hidden layer
• weights of the output layer
• biases of the hidden layer
• biases of the output layer

Now, once we have 100 different solutions, we can feed them to the model, evaluate them, and choose a bunch (let’s say 10) of the best ones. Then we mutate the solutions a bit, which was mentioned above as mutation, and create a new generation, which is simply N new solutions randomly picked from the top of the previous generation and slightly mutated.

However, here we use a little change to the original implementation of the algorithm. First, as we started with a small population of 100, let us allow the population to grow with every generation by some number. This is just a trick for faster convergence and better results over time.

The second trick is that, once in a while (say 20% of all the cases), we allow random initialization from scratch. Thus, even though we pick the top 10 solutions to create a new generation, there is still a chance for Albert Einstein to be born! Consequently, if they are there, those Einsteins can be picked and further mutated to create a new and better generation. The overall code cycle looks as follows:

To sum up, our slightly improved evolutionary algorithm does the following:

• randomly generates 100 sets of parameters for a given neural network architecture
• picks the best 10 of them
• randomly slightly mutates the top 10 and creates a new, slightly larger than a previous, population, with a 20% chance of completely random initialization
• repeats until it takes over the world!

And… voila! Our DarwinNet is ready! When it runs for 200 generations, it gives over 25% accuracy for the MNIST dataset on the test set. Not the best performance, however, a random guess would give 10% accuracy, so it is clearly doing something, as you can see in the figure below. The complete code can be found here. As mentioned above, adding a 20% chance of random initialization helps to improve the performance drastically, which corresponds to the characteristic “steps” on the plot.

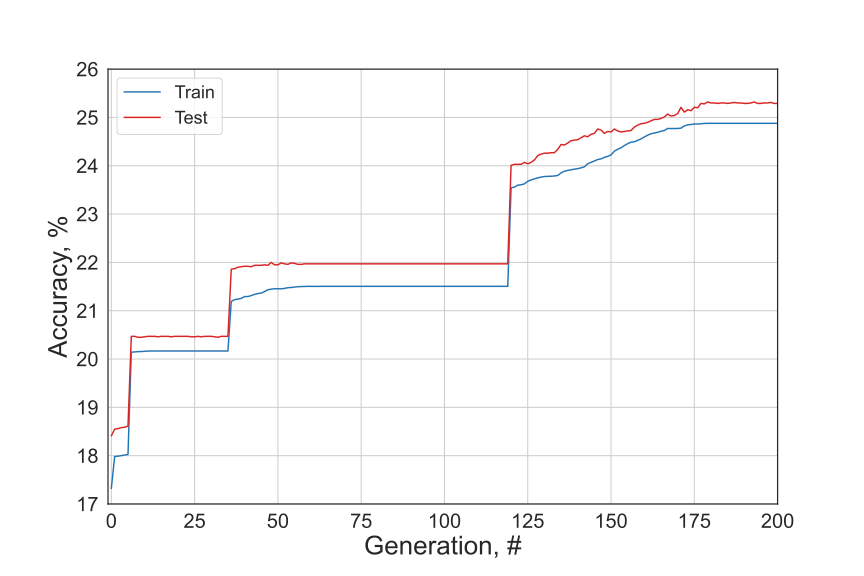
This post demonstrates how a genetic algorithm can be used to “train” the model on one of the benchmark datasets. Bear in mind that the code was written between office sword fights and coffee; there are no big ambitions here. Nevertheless, there are dozens of ways how to attain higher performance by different weight initialization, changing mutation rate, number of parents for each generation, number of generations, etc. Moreover, we can use our prior comprehension of neural networks and inject expert knowledge, i.e., pick the initial weights of the model using Kaiming initialization. This probably won’t help, but you’ve got the point, right? 😃

Of course, the idea of training neural networks using an evolutionary algorithm is not new. There are at least two papers by D. J. Montana & L. Davis and S. J. Marshall & R. F. Harrison from the last century sharing this idea, where they show genetic algorithm superiority over the backdrop. However, whatever happened happened. Nowadays, backpropagation-related attributes are fine-tuned to do their best, thus, their performance is dominant over genetic algorithms and other non-backprop rival methods eg. Hebbian learning or perturbation learning.

Another issue with the present implementation: it takes time… Well, maybe if it ran for over 4 billion years, the result would be better. 🙃

---

What if Charles Darwin Built a Neural Network? was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI