
From Concept to Code: Unveiling the ChatGPT Algorithm
Last Updated on January 22, 2025 by Editorial Team
Author(s): Ingo Nowitzky
Originally published on Towards AI.
For the past two years, ChatGPT and Large Language Models (LLMs) in general have been the big thing in artificial intelligence. Many articles about how-to-use, prompt engineering and the logic behind have been published. Nevertheless, when I started familiarizing myself with the algorithm of LLMs — the so-called transformer — I had to go through many different sources to feel like I really understood the topic.
In this article, I want to summarize my understanding of Large Language Models. I will explain conceptually how LLMs calculate their responses step-by-step, go deep into the attention mechanism, and demonstrate the inner workings in a code example.
So, let’s get started!
Table of contents
Part 1: Concept of transformers
1.1 Introduction to Transformers
1.2 Tokenization
1.3 Word Embedding
1.4 Positional Encoding
1.5 Attention Mechanism
1.6 Layer Norm
1.7 Feed Forward
1.8 Softmax
1.9 Multinomial
Part 2: Implementation in code
2.1 Data Preparation
2.2 Tokenization
2.3 Data Feeder Function
2.4 Attention Head
2.5 Multi-head Attention
2.6 Feed Forward of Attention Block
2.7 Attention Block
2.8 Transformer Class
2.9 Instantiate the Transformer
2.10 Model Training
2.11 Generate new Tokens
Part 1: Concept of Transformers
1.1 Introduction to Transformers
We cannot discuss the topic of Large Language Models without citing the famous paper “Attention Is All You Need” published by Vaswani et al. in 2017. In this article, the group of researchers introduced the attention mechanism and the transformer architecture that sparked the revolution in generative AI we experience today. Originally, the paper referred to machine language translation and introduced an encoder-decoder structure.

Fig. 1.1.1 on the left, shows the transformer as published in the paper, and on the right I marked the encoder and the decoder part. In machine language translation, the initial language is encoded by the encoder and decoded into the target language by the decoder.
In contrast, ChatGPT has a decoder-only architecture. Therefore, in the following, we will ignore the left side and fully concentrate on the decoder.
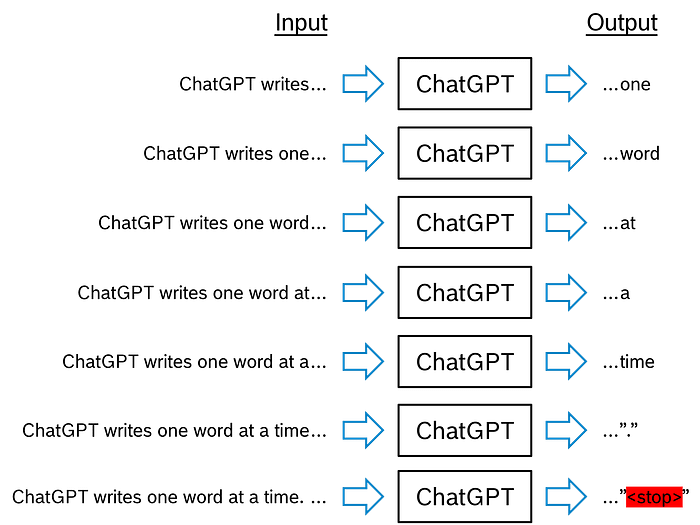
Before I start explaining the transformer, we need to recall that ChatGPT generates its output in a loop, one token after the other. Let’s assume we input the words “ChatGPT writes…” (yes, I know this context is unrealistically short). ChatGPT might output the token “…one” in the first cycle. The initial words plus the first output build the context for the second generation cycle, so the input is “ChatGPT writes one…”. Now, ChatGPT might output “…word”, which is concatenated to the existing context and inputted again. This loop goes on until the generated output is a stop token, which indicates that the response has reached its end and the generation loop is finished until the next user interaction.

Now, the big question is: what happens inside the magic box denoted “ChatGPT” in Fig. 1.1.2? How does the algorithm conclude which token to output next? This is exactly the question we will answer in this article.
Fig. 1.1.3 shows the processing steps of the transformer in a sequence and is an alternative illustration to that in the original paper (Fig. 1.1.1). I prefer using this image because it allows me to better structure the explanation.

In Fig. 1.1.3, we see the input into the transformer on the bottom left – the token sequence “ChatGPT writes…” – and the output of the transformer on the top right, which is “…one”. What happens between input and output?
- On the left side of Fig. 1.1.3, we find some preprocessing steps: tokenization, word embedding, and positional encoding. We will study these steps right after this introduction.
- In the middle part, we see the so-called attention block. This is where the context of the words and sentences is processed. The attention block is the magic of ChatGPT and the reason why the outputs of the bot are so convincing.
- On the right side of Fig. 1.1.3, we see that the output of the attention block is normalized (“Layer Norm”), fed into a neural network (“Feed forward”), softmaxed, and finally runs through a multinomial distribution. Later, we will see that, with those four steps, we calculate the probabilities for all tokens in our vocabulary to be the next output, and sample the actual output from the multinomial distribution according to those probabilities. But be patient — we will study this in the required details later in the article. For now, we accept that the output of this process is the token “one“.
With this overview in mind, let us go through the processing steps one by one in the next chapters.
1.2 Tokenization
Tokens are the basic building blocks for text processing in Large Language Models. The process of splitting text into tokens is called tokenization. Depending on the tokenization model, the received tokens can look quite different. Some models split text into words, others into subwords or characters. Independent of the granularity, tokenization models also include punctuation marks and special tokens like <start> and <stop> for controlling the LLM’s output to a user interaction.
The basic idea of tokenization is to split the processed text into a potentially large but limited number of tokens the LLM knows.

Fig. 1.2.1 shows a simple example. The context “Let’s go in the garden” is split into the seven tokens “let”, “ ‘ “, “s”, “go”, “in”, “the”, “garden”. These tokens are known to the LLM and will be represented by an internal number for further processing. Vice versa, when the LLM processes its output, it determines the next token through probabilities and composes the outputted sentences from the tokens of several generation cycles.
1.3 Word Embedding
So far, we have seen that the tokenizer splits the input sentences into tokens. Next, word embedding translates tokens into large vectors with usually several hundred or several thousand of dimensions, depending on the chosen model. In general, the higher the embedding depth (meaning larger vectors), the more information the embedding can capture.

In Fig. 1.3.1, we continue with our example: The tokenizer has split the sentence “Let’s go in the garden” into the seven tokens: “let”, “ ’ ”, “s”,…
The word embedding translates the tokens into the shown vectors. In Fig. 1.3.1, I denoted the number of dimensions with n, but in fact, I used 100 — a relatively small number!
The interesting point about word embedding is that it captures features of the tokens. One of the implications is that words with similar meanings get similar word embeddings and, therefore, are located nearby in the embedding space. This characteristic of tokens is automatically captured in the embedding process because words with similar meanings are used in similar contexts.

In Fig. 1.3.2, you see example words with an original embedding depth of 100. To plot the embeddings in the plane, I reduced the embedding vectors to dimension 2 with the principal component analysis (PCA). We see that words describing animals build one cluster, fruits build another cluster, and the same is true for tools, vehicles and sports. Thus, words with similar meanings are located nearby because they have similar embeddings.
But word embedding does not only capture similarities but also relations between words. As an example, in Fig. 1.3.3, you see a couple of adult-baby relations. Again, the original embeddings have a depth of 100 and were reduced to 2 using PCA.

We see that “puppy” relates to “dog” like “kitten” to “cat”, “toddler” to “human” or “calf” to “cow”. In each case, the baby word is in the top left and the adult word in the bottom right.
In this article, we take word embeddings as given because we have plenty of ready-to-use models (e.g., Word2Vec, GloVe, fastText). Nevertheless, I’d like to give you some high-level intuition about how word embeddings are calculated. Be aware that word embedding methods vary. The way sketched here is only one approach.

Word embeddings come from Encoder-Decoder neural networks. Typical for this architecture is that the inputs are compressed into a lower dimension, and from there we try to reconstruct information to a higher dimension. In Fig. 1.3.4, we have one node for each token in the vocabulary in the first and the last layer. We feed in a word or a couple of words into the encoder with a “1” in the respective node and “0” in all other nodes (one-hot encoding). The network compresses the information to a lower dimension — which equals the embedding depth — and from there tries to fulfill a task, e.g. predicting the next word in a sequence. If the calculated output is wrong, the weights of the model are updated via backpropagation. Once we achieve a sufficient accuracy, we take the lower dimensions’ weights as our word embeddings. Fig. 1.3.5 shows the embedding of “abacus” as an example. The embedding equals the weights behind the relations marked in bold.

1.4 Positional Encoding
Word embeddings do not keep track of the word order. The sentence “Today, I’m not happy, I am sad!” gets the exact same embedding vectors as the sentence “Today, I’m not sad, I am happy!” Of course, as humans we know that both statements have the opposite meaning, but the transformer does not!
This is where positional encoding comes into play. The main idea is to add a vector of the same size as the word embedding to each embedding vector. The positional vector specifies the position of the token in the context.

Fig. 1.4.1 continues our example of “Let’s go in the garden”. We see that for each of the seven tokens, a positional vector of equal size n is added. The positional vectors encode the 1st, 2nd, 3rd,… position in the given context. Therefore, the sum of the embedding vector and the positional vector holds information about the token and its position and is no longer independent of the word order. With positional encoding, the embedding vectors for “I’m not happy, I am sad!” and “I’m not sad, I am happy!” are no longer equal!
Now, how do we determine the positional vectors? In fact, there are different methods, and I will present only two of them:
- The method described in “Attention is all you need” by Vaswani et al. and
- A simplified method we use in our own coding.

Vaswani et al. propose to use sine and cosine functions to determine the positional vectors (Fig. 1.4.2 left). “pos” stands for the token position in the context: 1st token, 2nd token, 3rd token… and 2i and 2i+1 represent the odd and even embedding positions (the position within the positional vector). i runs from 0 to dmodel/2. For even embedding positions, we use the sine function, and for odd embedding positions the cosine function.
Fig. 1.4.2 right, shows the approach we use in our own coding (part 2). We make use of the PyTorch embedding module, which initializes to standard normal distributed values. This means we determine only the size of the positional vectors, but the vector values are random. Of course, once determined, we keep the positional vectors for the 1st, 2nd, 3rd,… position in the context fixed for the entire life of the LLM.
My personal impression is that the way positional vectors are calculated is less important for the performance of a transformer. However, it is crucial to use positional encoding, no matter how the vectors have been calculated.
1.5 Attention Mechanism
The attention mechanism is the heart of the transformer. It is the main reason why ChatGPT is so good at language processing. The key word in everything we discuss next is “context”.
The explanations in this chapter largely follow the ideas of Luis Serrano. I recommend his video series “Attention Mechanisms in LLMs” on YouTube to anyone who is interested.
1.5.1 Adjusting Word Embeddings to the Context
In human language, the context of words and sentences is very important to understand their meaning. Words can have different meanings in different contexts.
We have learned that word embeddings already take into account which words appear in connection with others more often. But word embeddings do not consider the context in a specific situation. We could say word embeddings have a static context, while we need a dynamic context that considers a specific sentence in its specific logical setting.
What a difference this makes can be studied with our mobile phones: The auto-complete function knows which word is most likely to follow the previous one. But without “understanding” the context, it starts outputting pure nonsense after three or four auto-completes (Fig. 1.5.1).

I guess we all agree: this is not the kind of response we expect from ChatGPT and other LLMs, right?
As mentioned briefly before, words can have different meanings in different contexts. As a demonstration, I’d like to quote a nice example from Luis Serrano.

Fig. 1.5.2 shows the word embedding as we get it from GloVe. As you can see, the word “apple” is neither near to the word “phone” nor to the word “orange”.
Now, imagine that we want to embed the sentence “apple unveiled a new phone”. As humans, we immediately know that the word “apple” stands for the tech company. How do we know? The specific context tells us, in particular the word “phone” (Fig. 1.5.3 left).

Next, imagine we want to embed the sentence “bring me an apple and an orange”. Again, as humans, we immediately know that this time we are talking about the fruit. In particular, the word “orange” is very helpful (Fig. 1.5.3 right).
How can we teach the computer to understand the context? This is what the attention mechanism is about! The core idea of attention is to modify the word embeddings in the very specific context. Therefore, we move words closer to those words in the embedding space that have a contextual relation.

Fig. 1.5.4 illustrates this core idea. In cases where we talk about the fruit, we move the word embedding of “apple” closer to “orange” while we shift it to “phone” in cases where we talk about the tech company.
How can we teach the computer to understand that “apple” is in relation either with “phone” or with “orange”? We need to calculate the word affinities between “apple” and all the other words in the context — including itself. This tells us where there is a strong affinity and where there is a weaker affinity. In fact, we calculate the word affinities between all combinations of tokens in the context (Fig. 1.5.5).
Finally, according to the affinities, we modify the word embeddings and move tokens with a stronger context closer.

OK, at this point, we know what we want to do once we know the word affinities. But how can we calculate them?
There are different methods for calculating the affinities — often called similarities. Here, we use the scaled dot product, which is also proposed in the paper “Attention Is All You Need”.
The scaled dot product is the dot product between the word embedding vectors a and b of the two tokens we evaluate, divided by the square root of the number of dimensions d of the word embedding vectors.

Fig. 1.5.6 shows the scaled dot product affinities for all token combinations in the context “bring me an apple and an orange”. As we see in the last column of the table, the sums of the rows add up to values between approximately 10 and 18. For the calculation of new word embeddings, it is more convenient to have sums of exactly 1. To achieve this, we use the softmax function:
According to Eq. 1.5.2, softmaxing means taking every value of a row to the e and dividing it by the sum of all values to the e. For our example, after applying softmax, we obtain the values shown in Fig. 1.5.7.

The affinities in Fig. 1.5.7 are the coefficients for calculating the context-adjusted „dynamic“ word embedding vectors: the higher the affinity, the greater the impact of a token on the new embedding. Let’s take „apple“ as an example (fourth row in Fig. 1.5.7):
We see that the context-adjusted „dynamic“ embedding of „apple“ is the sum of the products of all tokens in the context multiplied by the affinity of „apple“ to this specific token. In our example, the word embedding for „apple“ remains only 63.1% as it was and is 36.9% modified to better fit to its context.
Please remember that „bring“ etc. in Eq. 1.5.3 refer to the embedding vectors. In vector notation, Eq. 1.5.3 looks as follows:
The word embeddings for all other tokens in the context are adjusted accordingly.
1.5.2 Queries, Keys and Values Matrices
So far, we have learned how to calculate the context-adjusted new word embeddings in principle. If we look into the paper “Attention Is All You Need”, we find a modified approach with so-called queries Q, keys K and values V matrices. Let’s explore the idea behind this approach.

With the queries Q, keys K and values V matrices, we add an extra piece of backpropagation learning to the attention mechanism. The matrices help the model find better word embeddings in the given context. For the moment, let’s concentrate on the queries Q and keys K matrices. The values V come later.
So far, we have calculated the word affinities with a simple dot product according to Eq. 1.5.1.

Fig. 1.5.9 shows the calculation of the affinities in vector notation. For the moment, we concentrate on the multiplication and add the scaling with sqrt(d) in a later step. On the right side, we see how to calculate the dot product as a vector product: we take each entry of the apple embedding vector — now written as a row vector — and multiply it with the corresponding entries of the orange column vector, adding it all up. As a result, we receive a scalar.
If we recall from math, multiplying a vector with a matrix geometrically means a transformation. This transformation either stretches, compresses, rotates, or distorts the vector space.

In the example shown in Fig. 1.5.10, the space is only 2D, but in the attention algorithm, it can have any number of dimensions.
Why do we distort the vector space? The idea is to find a space that is ideal for representing the meanings of the tokens in the specific context.
In Fig. 1.5.10, we see that the left plane is OK for separating the two meanings of the word “apple”. The middle plane does a terrible job because, even if we move the word “apple” closer to the “phone” or the “orange”, we still have both representations very close. The third plane is clearly the best. It strongly supports separating the two meanings of “apple”.
With the queries Q and the keys K matrices, we let the transformer network find the optimal parameters for capturing the context of the tokens. Therefore, we add the two matrices to the calculation of the word affinities. Instead of multiplying the two embedding vectors directly, we multiply the product of the first embedding vector and the Q matrix (which is itself a vector) with the (transposed) product of the second embedding vector and the K matrix.

The product of the Q and K matrices in the middle of Fig. 1.5.11 (dotted box) is again a matrix that determines the linear transformation of the vector space. It is responsible for transforming the given space into the one that is optimal for the word embedding.
In summary, without the queries Q and keys K matrices, we use the given vector space. With Q and K, we find an optimal vector space and, consequently, a better dynamic word embedding according to the context of the input sentences.

Now, let me introduce the values matrix V and its function.
The vector space we found with the queries Q and keys K matrices is optimized for the word affinities. The values matrix V prepares the next step, which is calculating the probabilities of the next token following the given context. Therefore, we calculate a third linear transformation, which gives us a vector space optimized for this task.

So far, we have considered a toy example with only one token as input. With regard to the code example in part 2, I’d like to demonstrate how the matrix operations look like if we input a whole sentence. From there, it is easy to conclude how real-life matrix operations look.

In Fig. 1.5.14, the red 7×3 matrix X represents the input sentence and its embeddings. Each row corresponds to a token. The three columns are the three dimensions of the word embedding. Remember, real-life word embeddings have hundreds or thousands of dimensions!
The green 3×4 matrix is our queries matrix Q, which adds extra learning capabilities to the attention model. The three rows are fixed because they need to correspond to the embedding dimension of X. The four columns are called “head-size” and are a hyperparameter of the transformer model. Theoretically, we can choose any value. The more columns, the greater the learning capabilities.
The keys matrix K is always the same size as the queries matrix Q. Therefore, it has the dimension 3×4, but in Fig. 1.5.14, it is transposed to 4×3. The same is true for the yellow input matrix X, which corresponds to the red input matrix.
The multiplication operation returns a 7×7 matrix with the unscaled affinities for each possible token combination in the input sentence.

Fig. 1.5.15 continues the example from Fig. 1.5.14. The 7×7 matrix of unscaled token affinities is multiplied by the 7×3 input matrix X, which we have used earlier. The next step is to multiply the result by the 3×4 values matrix V. Again, the three rows correspond to the dimensions of the word embedding, and the four columns are the hyperparameter head-size. The multiplication results in a 7×4 matrix, which represents the word embeddings for calculating the probabilities of the next token to follow the input. We will explore in the next chapters how this is continued.
So far, we have omitted the scaling and softmaxing, but both steps are very simple and nearly identical to what we discussed in chapter 1.5.1.
Scaling is applied immediately after calculating the dot product of the queries matrix Q and the keys matrix K. We simply divide each value of the 7×7 matrix of unscaled affinities by the square root of the embedding dimension sqrt(d).

The next step after scaling is softmaxing. As with scaling, softmax is applied element-wise, and each element is divided by the sum of the respective row (as described in chapter 1.5.1).

Finally, let me summarize the steps of the attention matrix operations:
- We calculate the matrix product of X * Q * K_transposed * X_transposed and receive the unscaled affinities as a 7×7 matrix for seven input tokens.
- We divide each element of the 7×7 matrix by sqrt(d). This gives us the scaled affinities. Scaling is important for the softmax operation, as initial values should be small.
- Masking is an optional step mentioned in the original paper but not applied in ChatGPT. We ignore it.
- We softmax the matrix of scaled affinities. As a result, each row of the 7×7 matrix adds up to 1.
- Finally, we multiply the scaled and softmaxed 7×7 matrix of word affinities with X * V and receive the context-adjusted word embeddings as the final result (Fig. 1.5.18).

1.5.3 Multi-head Attention
All we have discussed so far is one single attention operation, called an attention head. But ChatGPT and other transformers have h-many of them. This means we calculate h queries, keys and values matrices in parallel. This gives us h attempts to find a good embedding, resulting in h 7×4 result matrices.
What do we do with the h result matrices? We concatenate them along the column axis and define a fully connected neutral network (“linear layer”) on top of the concatenated matrix with one node per column. The task of the linear layer is to weight the information in the concatenated result matrix: the useful information receive higher weights, while the less useful information is weighted less. This way, the transformer learns to pick the cherries.

With this, we have discussed all steps of the attention mechanism and can proceed with the next steps of the transformer.
1.6 Layer Norm
The attention mechanism gives us the “dynamic” embedding vectors — including the token positions and the relations between the tokens. In the next steps, we intend to calculate probability values for all tokens in our dictionary for being the next output of the LLM. Before we do this, we need a more technical step: Layer Norm.
Layer Norm is a technique commonly used in deep learning models that improves the model’s stability and convergence during training. It normalizes the values over a specified dimension — in our case, the embedding vectors — to have a mean = 0 and a standard deviation ≈ 1.
Let’s study a small example. Imagine we have two embedding vectors with an embedding depth of 5. This gives us a tensor x of size (2, 5). For demonstration purposes, we instantiate the tensor with random numbers between 0 and 10.
import torch
import torch.nn as nn
# Define word embedding vectors
x = torch.rand(2, 5)*10
print("Original input tensor:")
print(x)

Next, we instantiate a Layer Norm and define the input shape as the five values per embedding vector. We run the tensor x through the Layer Norm operation, output the transformed tensor normalized_x and check the new mean and the new standard deviation.
# Apply layer normalization
layer_norm = nn.LayerNorm(x.size()[1])
normalized_x = layer_norm(x)
print("Normalized input tensor:")
print(normalized_x)
print("\nMean:")
print(normalized_x.mean(dim=1))
print("\nStandard deviation:")
print(normalized_x.std(dim=1, unbiased=False))

We see that the values of normalized_x range from approximately -1.6 to +1.6, have a mean close to 0, and a standard deviation of 1.
1.7 Feed Forward
The feed forward layer is the computing engine in the transformer. It receives the normalized and context-adjusted (“dynamic”) word embeddings of our input and has the task of calculation probability values for the next token. It has as many input nodes as the embedding vectors have dimensions and one output node for each token in the vocabulary of the LLM. The layer is fully connected, so each embedding dimension has a relation to each token in the vocabulary.

Fig. 1.7.1 continues our example of “ChatGPT writes…”. We see the two input tokens “ChatGPT” and “writes”. Both tokens have embedding vectors of size n that feed their values into the n input nodes of the feed forward network. The task during model training is to learn the best weights that transform the embedding values to probability values for the next token to follow “ChatGPT writes…”.

With a given set of weights in the neural network, we can calculate the logits as the output of the feed forward layer. The token with the highest value is the potential winner of the search for the next token. So, theoretically, we could stop at this point! But in fact, this is not how ChatGPT works. If we stopped here, ChatGPT would give the exact same answer to an identical prompt. However, as we know, ChatGPT provides slightly different answers if we input the same prompt. Consequently, we need some randomness in our model. To give the model this characteristic, the transformer architecture has two more steps: softmax and multinomial.
1.8 Softmax
Recall, we want to give the LLM an indeterministic behavior. The first step in achieving this is to transform the logits from the previous step (feed forward) into probabilities between 0 and 1. In Fig. 1.7.2, we see all logits outputted from the network. With softmax, we take every value to the e and divide it by the sum of all values to the e.

What is the effect of softmaxing?
- Taking every value to the e helps us operating with negative logit values. Negative values close to 0 are transformed to values close to 1, while negative values approaching negative infinity are transformed into 0.
- Dividing each value by the sum of all values guarantees that the sum of all probabilities adds up to 1.

In summary, softmax transforms the logits to proper probabilities with values between 0 and 1, ensuring that the sum of all probabilities equals 1.
1.9 Multinomial
We have calculated the probabilities for each token in the vocabulary of the LLM. Now, it is time to draw a sample from a multinomial distribution function.

Fig. 1.9.1 illustrates the process of sampling:
- “aardvark” (the first word in the English dictionary) will be chosen with 0.1% likelihood.
- “bottom” with 0.3%.
- Most likely, “one” will be sampled because it has a likelihood of 95.1%.
- “word” has a likelihood of 4.6%.
- And “zygote” (the last word in the English dictionary) is almost impossible with a rounded likelihood of 0.0%
Here, we assume that “one” will be selected as the output. But we have learned that this is not guaranteed, and the tiny probability of seeing other outputs leads to the intended indeterministic behavior of the LLM!
Remember: Everything we discussed is one cycle through the transformer, and we have decided on the one token to output next. We repeat the same processes with the concatenated inputs again and again until the <stop> token is sampled as the next output!
Part 2: Implementation in code
So far, we have gone through a lot of theory. In the second part of the article, I want to demonstrate the theory in action and code with you a small GPT, including all components we have discussed before.
Please be aware that real-life applications run on ‘supercomputers’ and are trained with terabytes of data on thousands of GPUs for weeks. Here, we have only our PCs or laptops available, with one GPU at best. This means we need to scale down our expectations significantly. Nevertheless, the example will validate the theory and strongly deepen our understanding of the transformer architecture.
We are going to code a Fairy_Tale_GPT that learns English words from a collection of fairy tales (Brothers Grimm and H.C. Andersen). The data is freely available from the Gutenberg Project. In fact, the content of the data is less important than the availability of free-for-use text itself. You can use other data as well.
To keep the model relatively small, we will use the characters of the fairy tale texts as our tokens — not the words or word fragments. This keeps the model’s vocabulary small. I tried training the model on the word tokens as well — which works in principle — but the demand for training data is significantly higher than what we have available. Consequently, the learning success was very limited.
The Fairy_Tale_GPT is based on a project by Andrej Karpathy called nanoGPT. If you want to see Andrej’s original model and explanations, check out his YouTube video.
2.1 Data Preparation
First, we need the data. You can download the file ‘Fairy_Tales.txt’ from my Dropbox. Here, I assume that the file is stored in the same directory as the Jupyter Notebook containing the code.
# Libraries we will use in this notebook
import torch
import torch.nn as nn
from torch.nn import functional as F
import matplotlib.pyplot as plt
from IPython.display import clear_output
torch.manual_seed(1337)
# We load the text file's content into the variable 'text'.
with open('Fairy_Tales.txt', 'r', encoding='utf-8') as f:
text = f.read()
Please familiarize yourself with the data. Since it is stored in a simple .txt file, you can even open the file and read the fairy tales.
Let us check the file size in characters and print the first 300 characters.
# Let's see what we have in 'text'. How many characters?
print("Length of dataset in characters: ", format(len(text),','))
print()
# To get an impression of the file content, let's print the first 300 characters.
print(text[:300])

In text, we have a string of more than 807,000 characters. The fairy tales are stored one below the other, and the first fairy is THE GOLDEN BIRD.
2.2 Tokenization
As discussed in chapter 1.2, tokenization is the process of splitting the data into words, word fragments, or characters, finding the unique tokens, and assigning them unique numbers. The idea behind tokenization is to limit the size of the LLM’s vocabulary and prepare the model to process those tokens.
The first step of our tokenization process is to find the unique characters in the fairy tales.
# Find a list of all unique characters in the text.
# The data type 'set' eliminates all doubles.
chars = sorted(list(set(text)))
vocab_size = len(chars)
print(''.join(chars))
print('\nSize of vacabulary: ', vocab_size)

We have 80 unique characters, including punctuation marks and other special characters. These are the base units the LLM needs to learn.
Next, we need an encoding and a decoding function to translate the tokens — in this case characters, in other applications words or word fragments — into token numbers. As a first step, we define two dictionaries: one for token → number and one for number → token.
# Dictionary: Characters (c) to numbers (i)
ctoi = {c:i for i,c in enumerate(chars)}
# Dictionary: Numbers (i) to characters (c)
itoc = {i:c for i,c in enumerate(chars)}
Before we proceed with the encoding and decoding functions, we should consider how we present the data to the LLM. Knowing that we have a limited amount of data, we should make the best use of it.
Later, we will split the data into a training and a validation dataset. Accepting, for example, the first 90% as training data and the remaining 10% as validation data would mean to validate with different fairy tales than used for training. This does not sound ideal. Therefore, we split our full dataset into paragraphs. This allows us to mix the paragraphs when dividing the data into training and validation datasets.
The split_text_into_paragraphs() function does exactly this.
# Split the full text into paragraphs of min 50 words
# Return a list of lists
def split_text_into_paragraphs(text, min_words=50):
lines = text.split('\n')
current_paragraph = ""
paragraphs = []
for line in lines:
# Add line to the current paragraph buffer
current_paragraph += line + "\n"
# If current paragraph has at least 'min_words' words, store it and reset
if len(current_paragraph.split()) >= min_words:
paragraphs.append([current_paragraph])
current_paragraph = ""
# Add left-overs
if current_paragraph:
paragraphs.append([current_paragraph])
return paragraphs
The function accepts a text variable and a minimum number of words min_words. It splits the text by the line-break separator \n and processes all text snippets, concatenating each snippet to the buffer variable current_paragraph. If the concatenated text is at least min_words long, it is considered a paragraph and added as a list. The function’s final output is a list of lists containing the text paragraphs of minimum length.
Now we can continue encoding and decoding.
The encode() function accepts the list of lists with strings as the paragraphs variable and the dictionary ctoi (read “c to i”). It enumerates the paragraphs, takes the texts, and encodes them based on the ctoi dictionary. Finally, the encodings are appended to a list and outputted. The function returns a list of lists of integers.
# Encode strings to list of integers
def encode(paragraphs, ctoi):
"""
Translates a list of lists with text into a
list of lists with token numbers.
"""
encoded_paragraphs = []
for paragraph in paragraphs:
# Get text from inner list
text = paragraph[0]
# Translate tokens to integers
encoded = [ctoi[c] for c in text if c in ctoi]
# Add the encoded paragraph to the list
encoded_paragraphs.append(encoded)
return encoded_paragraphs
# Decode list of numbers (li) to string (s)
def decode(li, itoc):
"Translates a list of integers back to a sting."
# Translate integers to tokens
tokens = [itoc[i] for i in li]
# Join tokens to a string
decoded_text = "".join(tokens)
return decoded_text
The decode() function is simpler. It takes a list of integers li, and the itoc (“i to c”) dictionary, and decodes the integer token numbers into stings. Finally, the strings are concatenated to decoded_text and returned as output.
If you are following the code, please test the functions. You will see that they fulfill their tasks.
The next step is to encode the whole dataset. This transforms the list of lists of strings into a list of lists of integers.
# Encode the full dataset
data = encode(split_text_into_paragraphs(text), ctoi)
Now, we shuffle the paragraphs (of integer token numbers) and split them into the training dataset train_data_list and the validation dataset val_data_list.
import random
# Shuffle data
random.shuffle(data)
# Split data into train (90%) and val (10%)
n = int(0.9*len(data))
train_data_list = data[:n]
val_data_list = data[n:]
So far, both datasets are Python lists of integer numbers. But for the LLM, we need PyTorch tensors. Since we are not going to further modify the validation dataset, we can transform it into a PyTorch tensor immediately. To do this, we flatten the list of lists of integers into a single list of integers flat_list and load the data into a PyTorch tensor.
# Flatten the list of lists into a single list
flat_list = [token for paragraph in val_data_list for token in paragraph]
# Load validation data into PyTorch tensor
val_data = torch.tensor(flat_list, dtype=torch.long)
We don’t do the equivalent operations for the training data yet. The reason is that I prefer to shuffle the paragraphs as part of the training loop. This gives the data a little more variance and data augmentation.
2.3 Data Feeder Function
The data feeder provides the model with the training data and the corresponding labels, or, in the case of validation, with the validation data.
First, we define three important model parameters.
batch_sizedetermines how many chunks of data are processed in parallel during one training loop. We set it to 64.block_sizedefines the length of the context the model sees when it calculates the next token. We set it to 128 tokens.deviceis either ‘cuda’ or ‘cpu’ and determines whether the model is processed on the CPU or the GPU of your computer.
batch_size = 64 # Number of independent sequences we process in parallel
block_size = 128 # Length of token sequences as context
device = 'cuda' if torch.cuda.is_available() else 'cpu' # Use GPU instead of CPU, if available
print(device)
# Function, that provides the model with a batch of training or validation data
# and the corresponding labels (the correct next token)
def get_batch(ValTrain):
# Define data source
if ValTrain == "val":
data = val_data
else:
# Flatten and shuffle the training data (data augmentation)
shuffled_data = [
token for paragraph in random.sample(train_data_list, len(train_data_list))
for token in paragraph
]
data = torch.tensor(shuffled_data, dtype=torch.long)
# Generate sliding windows over the data
sliding_windows = [
data[i:i + block_size + 1]
for i in range(0, len(data) - block_size, block_size // 2) # Step size = block_size // 2
]
# Select batch_size many windows randomly
selected_windows = random.sample(sliding_windows, batch_size)
# Split each window into input (x) and target (y)
x = torch.stack([window[:-1] for window in selected_windows]) # All but the last token
y = torch.stack([window[1:] for window in selected_windows]) # All but the first token
# Move tensors to device (CPU/GPU)
x, y = x.to(device), y.to(device)
return x, y
The get_batch() function expects the variable ValTrain, which should be either ‘val’ or ‘train’. If it is set to ‘val’, the function returns validation data and simply loads the the tensor val_data into the data variable. In cases where ValTrain is set to any other value, the function returns training data. Remember, we have not prepared the training data tensor yet and need to do so now. To achieve this, we shuffle and flatten the list of lists of integer token numbers and load it into shuffled_data. Next, we load the data into a PyTorch tensor and save it in the data variable.
The next step in the get_batch() function is to create sliding windows over the data. Intentionally, the windows overlap by half of the block_size. We define the sliding windows as a list of lists, where each inner list contains block_size many tokens, and store them in sliding_windows. Next, we randomly select batch_size many samples and stack them into two-dimensional tensors with the training data x and the corresponding labels y, shifted by one token. This way, the labels y contain the next token following the training data x.
Both tensors, x and y, are shifted to device and returned as the results of the get_batch() function.
When we test the get_batch() function, we see that the input_data and the labels are tensors of size (64, 128) and that labels is shifted by one token to the right.
# Test the feeder function
input_data, labels = get_batch('train')
print("Shape of input_data:", input_data.shape, "\n")
print("Input_data:\n", input_data, "\n")
print("labels:\n", labels, "\n")

To confirm that everything works correctly, we decode the first row of input_data back into plain English.
# Decode the first row of the input data back into English
print(decode(input_data.cpu().numpy()[0],itoc))

2.4 Attention Head
Next, we start coding the attention mechanism, beginning with a single attention head and the corresponding matrix operations as discussed in chapter 1.5.2.
The attention head is part of the multi-head attention, which itself is part of the attention block. Fig. 2.4.1 shows the attention heads’ positions in the multi-head attention. We will refer to the figure frequently in the next steps, so keep it in mind.

We start the coding with two additional hyperparameters:
n_embddefines the embedding depth for all tokens (chapter 1.3). We set it to 192.dropoutis the percentage of parameters we randomly set to zero during training. This serves as a measure against overfitting. Since the model tends to memorize the data instead of generalizing the patterns (presumably due to insufficient size of dataset), we setdropoutto the relatively high value of 0.4.
The attention head is implemented as its own class called Head(), with a __init__() and a forward() method. In __init__(), we define the queries Q, keys K, and values V matrices, each as a nn.Linear() layer of size (n_embd, head_size). The nn.Linear() layer manages the weight matrices and processes the matrix multiplications of Q, K and V with the input data x. It is important to understand that the variables self.query, self.key, and self.value represent the matrix products x @ Q, x @ K, and x @ V, and not just the weight matrices (Fig. 1.5.14 and 1.5.15).
Additionally, in __init__() we define a register_buffer. This is a kind of method that saves a tensor to the module’s state dictionary but excludes it from training. This means the values are not updated through backpropagation. Here, we use it to store a lower triangular matrix tril of size (block_size, block_size) with values set to 1. We will use it later in the calculations.
# More hyperparameters
n_embd = 192 # The embedding depth for each token
dropout = 0.4 # The percentage of weights we set to 0 during training for regularization
# Class for single attention head
class Head(nn.Module):
""" Single head of self-attention """
def __init__(self, head_size):
super().__init__()
self.key = nn.Linear(n_embd, head_size, bias=False) # (C,H)
self.query = nn.Linear(n_embd, head_size, bias=False) # (C,H)
self.value = nn.Linear(n_embd, head_size, bias=False) # (C,H)
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size))) # Lower triangular matrix
self.dropout = nn.Dropout(dropout) # Ignore a portion of neurons per training loop --> prevent overfitting
def forward(self, x):
B,T,C = x.shape # C=n_embd
k = self.key(x) # x @ key (B,T,C) @ (C,H) --> (B,T,H)
q = self.query(x) # x @ query (B,T,C) @ (C,H) --> (B,T,H)
# compute attention scores ("affinities")
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B,T,H) @ (B,H,T) -> (B,T,T)
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B,T,T) # Fill with '-inf' where template has 0
wei = F.softmax(wei, dim=-1) # (B,T,T)
wei = self.dropout(wei) # (B,T,T)
# Perform the weighted aggregation of the values
v = self.value(x) # x @ value (B,T,C) @ (C,H) --> (B,T,H)
out = wei @ v # (B,T,T) @ (B,T,H) --> (B,T,H)
return out
In the forward() method, we calculate the matrix products x @ K and x @ Q and save them in the variables k and q. Both results have the dimension batch size (B) x number of tokens (block size, T) x head size H, in short (B, T, H). Please compare Fig. 1.5.14 and 1.5.15 in chapter 1.5.2 for reference.
Next, we calculate the scaled word affinities with q @ k_transpose / sqrt(C) and store them in wei (Fig. 1.5.16). This gives us a tensor of size (B, T, T). Now, we use the lower triangular matrix tril (size (T, T)) as a template for torch.masked_fill() to set each value of wei where tril has the value 0 (above the diagonal) to -inf.
Why do we do this? In the next step, we apply softmax to wei, and softmaxing -inf results in 0. This effectively eliminate the word affinities for token combinations that have not been processed from the wei matrix. With this step we exclude knowledge in the training that the model cannot have in production.
With self.dropout(wei), we randomly set a specified share of weights to 0 as a measure against overfitting.
Finally, we calculate x @ V as v and the context-adjusted word embeddings with out = wei @ v. This is the return value of the function and is of size (B, T, H).
2.5 Multi-head Attention
As described in chapter 1.5.3, multi-head attention utilizes n_head attention heads in parallel. Additionally, we apply a linear layer to weight the more beneficial attention head responses higher and the less beneficial lower.

Fig. 2.5.1 shows all process steps of multi-head attention in the sequence of processing.
# Class that bundles 3 attention heads
class MultiHeadAttention(nn.Module):
""" Three heads of self-attention in parallel """
def __init__(self, num_heads, head_size):
super().__init__()
self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)]) # Just a container
self.weighting = nn.Linear(n_embd, n_embd) # Linear layer to weight the attention heads
self.dropout = nn.Dropout(dropout) # Prevent overfitting
def forward(self, x):
out = torch.cat([h(x) for h in self.heads], dim=-1) # Feed parallel attention heads and concatenate results
out = self.dropout(self.weighting(out)) # Weighting the attention head results and dropout
return out
We bundle all multi-head activities in the class MultiHeadAttention().
In the __init__() method, we define a list of num_heads attention heads and save it in the variable self.heads. The linear layer for weighting the heads’ responses according to their usefulness is stored in self.weighting. Finally, we define another dropout layer in self.dropout.
In the forward() method, we take the normalized and position-enriched word embeddings of the input context as x and run them independently through the three attention heads. Then, we concatenate the responses along the column axis, resulting in a tensor of 3 x head_size columns (which is equivalent to n_embd). This tensor is cached in out and fed into the linear layer self.weighting(), which regulates the weights of the responses. Lastly, the weighted head responses pass through dropout, where 40% of the tensor elements are set to zero to prevent overfitting.
2.6 Feed Forward of Attention Block
The feed forward layer in the attention block has a general computational purpose and consists of four steps. Therefore, we define it as its own class FeedForward().

It takes the normalized multi-head responses as input x and passes them through two fully connected neural network layers: the first has a size of (n_embd, 4 x n_embd), and the second has a size of (4 x n_embd, n_embd). This means the layers are expanded by factor 4 and compressed back to the original size — simply to add additional learnable weights. Between the layers, we include a ReLU activation function to introduce a non-linear behavior into the network.
# A linear layer for general calculation purpose
class FeedForward(nn.Module):
""" Simple linear layer followed by a non-linearity """
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential( # Sequence of steps
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout))
def forward(self, x):
return self.net(x)
In the final step, we apply dropout again as a measure against overfitting.
2.7 Attention Block
Now it’s time to compose the attention block from the previously defined components, as shown in Fig. 2.7.1.

Again, we define a new class called Block(). In its __init__() method, we calculate the free dimension of the Q, K and V matrices — the head_size — as the quotient of embedding depth n_embd and the number of attention heads n_head. Then, we instantiate the MultiHeadAttention() class in self.sa and the FeedForward() class in self.ffwd. Additionally, we define two normalization layers in the variables self.ln1 and self.ln2.
# Only one pass-through. Loop is specified in the Transformer class
class Block(nn.Module):
""" Attention block """
def __init__(self, n_embd, n_head):
super().__init__()
head_size = n_embd // n_head # Free dimension of key, query and value matrices
self.sa = MultiHeadAttention(n_head, head_size)
self.ffwd = FeedForward(n_embd)
self.ln1 = nn.LayerNorm(n_embd)
self.ln2 = nn.LayerNorm(n_embd)
def forward(self, x):
x = x + self.sa(self.ln1(x)) # Residual/skip connection
x = x + self.ffwd(self.ln2(x)) # Residual/skip connection
return x
In the forward() method of the class, we receive the position-enriched word embeddings of the input to the LLM as x. We normalize x using self.ln1() and pass the result through the multi-head attention self.sa(). Then, we add a skip connection, meaning we add the original values of x — without normalization and self-attention — to the results. This stabilizes training and minimizes the problem of vanishing gradients.
Next, we pass the updated x through the second normalization layer self.ln2 and then through the feed forward class self.ffwd. We add another skip connection — this time the variable x contains the results before layer norm 2, not the original input tensors to forward() — and output the result.
2.8 Transformer Class
Before coding the Transformer() class, let’s recall how data flows through the architecture during training and in production.
Fig. 2.8.1 shows one cycle during training. We feed the input data into the model and assign it the task of predicting the next token following to the input data. The true next token serves as our label data. We run the input data through the model up to the final Feed forward layer, which gives us the logits representing the token probabilities.
Next, we use logits and true labels to compute the cross entropy loss. The higher the loss, the greater the need to update the model parameters. Using the loss function, we backpropagate through the model and update the weights.

During production, we do not have any labels. Instead, we are interested in the model’s output as the response to the user interaction. We feed the model with the input data and pass it through the model – this time with two additional steps compared to training. After the Feed forward layer, the logits are softmaxed and used in the Multinomial distribution function to sample the next token (chapter 1.8 and 1.9).

According to the different approaches during training and production, the Transformer() class has three methods: __init__(), forward() and generate().
Again, we start with two additional hyperparameters:
n_headdefines the number of parallel attention heads in the Multi-head attention. As mentioned earlier, this variable is set to 3.n_layerspecifies the number of sequential attention blocks (e.g. Fig. 2.8.2). In our model, this is set to 4.
Within the __init__() method of the Transformer() class, we define the word embedding and the positional encoding (chapter 1.3 and 1.4). For both, we use of the nn.Embedding method, which creates a lookup table of the specified size and assigns the input values uniquely to the rows of this table.
- For the the word embedding, the lookup table has the size of
vocab_sizexn_embd, meaning that each token in the vocabulary corresponds to a specific row with the word embedding values. - For the positional encoding, the lookup table has the size
block_sizexn_embd, where each row of the table represent the position of the token in the input context. Since we considerblock_sizemany tokens in the context, we need to differentiate as many positions. The number of columns again equals the embedding depth.
In both cases — word embedding and positional encoding — nn.Embedding initializes the tables with random values, which remain fixed throughout the life of the LLM.
The next step in __init__() is to define a sequence of n_layer Attention blocks in the variable self.blocks. Since n_layer is set to 4, the data passes through 4 Attention blocks sequentially before continuing to the final Layer Norm (Fig. 2.8.1 and 2.8.2).
Next, we define the final Layer Norm and the Feed forward layer as a nn.linear layer in the variables self.final_ln and self.final_ff. The Feed forward layer translates the context-adjusted word embeddings into the probabilities of each token in the vocabulary and is of equivalent size (chapter 1.7 and Fig. 1.7.1).
# More hyperparameters
n_head = 3 # Number of attention heads in multi-head attention
n_layer = 4 # Number of attention blocks
# Main class embracing all modules
class Transformer(nn.Module):
# When we instantiate from the Transformer class
def __init__(self):
super().__init__()
self.token_embedding_table = nn.Embedding(vocab_size, n_embd) # Word/token embedding
self.position_embedding_table = nn.Embedding(block_size, n_embd) # Positional embedding
self.blocks = nn.Sequential(*[Block(n_embd, n_head) for _ in range(n_layer)]) # Stack of attention blocks
self.final_ln = nn.LayerNorm(n_embd) # Final layer norm
self.final_ff = nn.Linear(n_embd, vocab_size) # Final linear layer
# When we pass data through an instance of the Transformer class
def forward(self, input, targets=None): # input and targets are both (B,T)-dimensional tensors of integers
B, T = input.shape # Dimensions of input data: batch x tokens
tok_emb = self.token_embedding_table(input) # (B,T,C)
pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
x = tok_emb + pos_emb # (B,T,C), Python automatically adds dimension B to pos_emb
x = self.blocks(x) # (B,T,C)
x = self.final_ln(x) # (B,T,C)
logits = self.final_ff(x) # (B,T,vocab_size)
# Only if targets are defined --> loss calculation
if targets is None:
loss = None
else:
B, T, C = logits.shape # Get dimensions of output
logits = logits.view(B*T, C) # Transform to two dimensions for cross_entropy function
targets = targets.view(B*T) # Transform to one dimension for cross_entropy function
loss = F.cross_entropy(logits, targets) # Calculate the losses
return logits, loss
# When we generate new text (production)
def generate(self, idx, max_new_tokens):
# idx is (B, T) tensor of indices
for _ in range(max_new_tokens): # Concatenate max_new_tokens outputs
# Crop idx to the last block_size tokens
idx_cond = idx[:, -block_size:]
# Get the predictions
logits, loss = self.forward(idx_cond)
# Focus only on the last token
logits = logits[:, -1, :] # becomes (B, C)
# Apply softmax to get probabilities
probs = F.softmax(logits, dim=-1) # (B, C)
# Sample from the distribution
idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
# Append sampled index to the running sequence
idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
return idx
The forward() method is used for the training of the LLM and is also called in the generate() method. It receives the input data and, optionally, label data in the variable targets. Both are tensors of size (B, T), meaning one row for each of the batch_size many samples and one column for each of the block_size many tokens.
We pass the input data through the self.token_embedding_table(), which adds the corresponding word embedding values from the lookup table to each token in all of the batches in a separate dimension. This extends the size of the tensor from (B, T) to (B, T, C), where C represents the embedding depth.
Similarly, self.position_embedding_table() adds the embedding values to each of the T positions 0, 1, …, T-1 in the input context, resulting in a tensor of size (T, C). Next, we add the token embedding tok_emb and the positional embedding pos_emb to form the variable x. Python automatically extends the pos_emb tensor by the dimension B and repeats the content of the original tensor B-times. Thus, x has the size (B, T, C).
According to Fig. 2.8.1, the next step is the Attention block. We pass x through self.blocks(), then through the final Layer Norm self.final_ln(), and finally through the final Feed forward layer self.final_ff(), which gives us the tensor with the logits of size (B, T, vocab_size). As discussed earlier, the linear layer translates the word embeddings into probabilities values for the tokens in the vocabulary.
If targets is specified — during training — the next step is to transform the logits from a 3-dimensional tensor to 2 dimensions. With logits.view(B*T, C), the B batches of data are stacked on top of of each other (caution: C does now represent the vocab size). We apply the same transformation on targets, reducing it from 2D to 1D. Both transformation are required to match the input format of F.cross_entropy(), which calculates the loss value. As always, the goal of the training process is to minimize the loss. This is equivalent to getting the best prediction quality for the next token to follow the input context stored in targets.
During production, we use the generate() method. It receives a tensor of context indices idx and the number of tokens to generate max_new_tokens. The tensor idx has the size (B, T). This means we can generate B batches of outputs in parallel, but B can also be 1 if idx has only one row. The indices in idx represent the token numbers of the input context according to the dictionaries itoc and ctoi we specified in the tokenization (chapter 2.2). The parameter max_new_tokens is an “artificial” one — you will not find it in real life LLMs. We need it because we have no stop tokens in our training data, therefore we need a “hard” way to stop the process of text generation.
In generate() we have a loop with max_new_tokens repetitions. Inside, we condition idx in case it has more tokens than our specified block_size. In this case, we take the last block_size many tokens. Next, we call self.forward() with the input idx_cond. The method returns the logits and the loss (we do not use the loss any further). The logits tensor has the size (B, T, C) (C represents the vocab size) and contains the predicted probability values for each token in the input context — even for those where we know the next token because we can read it in the user input. That is why we limit logits to the last token with logits[:, -1, :]. This step reduces the tensor’s dimension to (B, C).
According to Fig. 2.8.2 the next steps are Softmax and Mutinomial. Correspondingly, we softmax the logits over the C dimension. Now, we have real probabilities, adding up to 1 over the vocabulary, and save them in probs. Next, we input probs into torch.multinomial() which samples one index according to the given probabilities. This new index is the essence of all we did because it represents the next token! We concatenate it to the given context in idx and repeat the process max_new_tokens times.
2.9 Instantiate the Transformer
We have defined all classes of the Fairy_Tale_GPT. So, we can instantiate it and give it a first try before we start the model training.
Instantiating is very simple. We call the Transformer() class and push it to device. For our information, we enumerate the model.parameters() with a generator comprehension and add up all elements. This gives us the number of parameters in our LLM.
# Instantiate an object from the Transformer class
model = Transformer().to(device) # 'model' lives on the device, in my case the GPU
# Print the number of parameters of the model
print(format(sum(p.numel() for p in model.parameters()),","), 'parameters')

We see that our Fairy_Tale_GPT has a little more than 1.8 million parameters.
Now, I am curious to see a first output of the LLM — knowing that the model hasn’t seen any training yet. The generate method requires a tensor of starting indices as the context. Therefore, we define a 2-d tensor containing only one 0 (random choice) and store it in context. Next, we call the generate method of the instance with model.generate(), provide it with the context and specify the max_new_tokens parameter as 200. With [0] we unpack the first batch (technically required, although we have only one batch) and transform the given PyTorch tensor into a Python list with .tolist(). Finally, we decode() the list of integer token numbers into characters according to our dictionary itoc (chapter 2.2), save the result in untrained_results and print it.
# Generate from the model
context = torch.zeros((1, 1), dtype=torch.long, device=device)
untrained_results = decode(model.generate(context, max_new_tokens=200)[0].tolist(),itoc)
print(untrained_results)

Well, the output does not exactly look like English words from fairy tales, does it? It is more a sequence of purely random characters from our vocabulary. Let’s check if training can improve the result.
2.10 Model Training
Before we actually code the training loop for the LLM, we define some more hyperparameters and a helper function for calculating the losses during training.
eval_itersdefines how many training iterations are averaged in the calculation of the losses. We set it to 10.learning_rateis the step width for updating the model parameters and is set to 1e-3. Since we use a learning rate scheduler,learning rateis only the starting value. The actual learning rate is reduced according to a cosine function during training to improve the model stability and prevent overfitting.max_itersdefines the number of training loops. It is 10,000 iterations.eval_intervaldefines after how many iterations the training code prints the actual loss values, outputs the corresponding plot, and a text sample. We receive those updates every 200 iterations.context_tensoris the matrix of indices we already used in chapter 2.9. It is required for the sample text generations during the training.
# Cosine annealing learning rate scheduler
from torch.optim.lr_scheduler import CosineAnnealingLR
# More hyperparameters
eval_iters = 10 # How many iterations do we average in the loss calculation
learning_rate = 1e-3 # Starting step size for learning
max_iters = 10000 # Number of training loops
eval_interval = 200 # How often evaluate the model performance
context_tensor = torch.zeros((1, 1), dtype=torch.long, device=device)
# Function calculates losses and averages results over eval_interval values
@torch.no_grad() # Do not calculate any gradients for this function
def estimate_loss():
out = {} # Empty dictionary for the results
model.eval() # Set model to evaluation mode
# Calculate loss for training and validaton data
for split in ['train', 'val']:
losses = torch.zeros(eval_iters) # Set to 0 for start
for k in range(eval_iters): # 10 loops
X, Y = get_batch(split) # Get training data
logits, loss = model(X, Y) # Call model and get logits and losses
losses[k] = loss.item()
out[split] = losses.mean() # Save average under key 'train' or 'val'
model.train() # Set model in training mode
return out
The estimate_loss() function computes the validation and the training loss during the model training. The decorator @torch.no_grad() turns off the gradient tracking in PyTorch for the decorated function.
Inside estimate_loss() are two nested loops. The outer loop iterates over the two values ‘train’ and ‘val’ which specify training and validation. The inner loop iterates over the range(eval_iters) (which means 10 iterations) and calls the get_batch() function either for ‘train’ or for ‘val’. The returned data is fed into the model() which returns the logits and the loss. Here, we are interested in the loss and save it to the tensor losses. Outside the inner loop we compute the average over the ten values in losses and save it either in out[‘train’] or out[‘val’]. Finally, out is the return value of the function.
For the model training we define an optimizer and a learning rate scheduler. The optimizer updates the model parameters according to the gradients from backpropagation and the learning rate. We choose the AdamW optimizer which is very common. The AdamW optimizer allows to specify weight_decay which adds the sum of all weights (times the specified factor 0.03) to the loss function. This pushes the model to prefer smaller weights — again a measure against overfitting.
As described in the hyperparameter definition, the learning rate scheduler reduces the learning rate from learning_rate (1e-3) to eta_min (1e-5) over the course of max_iters (10,000) training iterations.
# Create a PyTorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate, weight_decay=0.03)
# Cosine annealing learning rate scheduler
scheduler = CosineAnnealingLR(optimizer, T_max=max_iters, eta_min=1e-5) # Minimal LR is 1e-5
Inside the training loop we use three lists to collect the losses. All three lists are not essential to the training itself but used to inform about the training progress every eval_interval iterations. In loss_lst_train we collect the training loss, in loss_lst_val the validation loss and in loss_lst_x we store the actual iteration numbers for the x-axis of the plot.
The training loop runs from 0 to max_iters(-1) and stores the actual loop counter in iter. We call the get_batch() function for training data and store the returned input data in xb and the corresponding labels in yb. Both are fed into the model which returns the logits and the loss. Next, we set all gradients to None with optimizer.zero_grad(set_to_none=True) and compute the new gradients with loss.backward(). We update the model parameters with optimizer.step() and reduce the learning rate incrementally according to a cosine function with scheduler.step().
# Empty lists of losses
loss_lst_train = []
loss_lst_val = []
loss_lst_x = []
# Train the model over max_iter loops
for iter in range(max_iters):
# Get a batch of training data
xb, yb = get_batch('train')
# Run the transformer model
logits, loss = model(xb, yb)
# Zero the gradients
optimizer.zero_grad(set_to_none=True)
# Calculate the gradients
loss.backward()
# Optimize parameters through backpropagation
optimizer.step()
# Update the learning rate with the scheduler
scheduler.step()
# Evaluate and print losses
if iter % eval_interval == 0 or iter == max_iters - 1:
# Caluculate losses
losses = estimate_loss() # Call evaluation function
loss_lst_train.append(losses['train'].item()) # Append to training list
loss_lst_val.append(losses['val'].item()) # Append to validaton list
loss_lst_x = list(range(len(loss_lst_train))) # Prepare the x values for plotting
# Plot
clear_output(wait=True) # Clear output in jupyter
print(f"Step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
plt.figure(figsize=(5,3))
plt.plot(loss_lst_x,loss_lst_train,label='train')
plt.plot(loss_lst_x,loss_lst_val,label='val')
plt.xlabel('steps (x' + str(eval_interval) + ')')
plt.ylabel('losses')
plt.title('Training and validation loss')
plt.legend()
plt.show()
# Do a test generation to observe the quality
print('Test word generation:')
print(decode(model.generate(context_tensor, max_new_tokens=200)[0].tolist(),itoc))
All operations inside the if-condition are optional and used to inform about the progress during training. In the first step we call the estimate_loss() function and collect the losses in the specified lists. In the middle part of the code, we clear the output in the Jupyter notebook with clear_output() and plot the training and validation loss as a matplotlib line chart over the iteration numbers. In the lower part we generate a test text in the same way as we did in chapter 2.9.
The output of the code at the end of the 10,000 training iterations looks something like this:

After model training, we should save the parameters. Otherwise they will be lost after deleting the model from the PC’s memory and we would have to restart the training.
torch.save(model.state_dict(), 'Name_of_your_choice.pth')
The model.state_dict() saves the model’s parameters but not the model architecture. We need to load this first before we can load the parameters.
2.11 Generate new Tokens
Before we start the token generation, let us load the model parameters. Here, we assume that model itself is already loaded.
# Load the saved model state
state_dict = torch.load('Name_of_your_choice.pth')
# Load the parameters into the transformer model
model.load_state_dict(state_dict)

Now, let’s compare the LLM’s output before and after the training.
# Print output before training
print('Model output before training:')
print(untrained_results)
# Print output after training
context = torch.zeros((1, 1), dtype=torch.long, device=device)
trained_results = decode(model.generate(context, max_new_tokens=500)[0].tolist(),itoc)
print('\nModel output after training:')
print(trained_results)

For the output of the untrained LLM we use the variable untrained_results, which we filled before the training. The text trained_results is generated ‘right now’ through the model.generate() method. Please check chapter 2.9 for an explanation of the line of code.
While in untrained_results the sequence of characters is purely random, we can clearly recognize an English word structure in trained_results, although some words are fantasy and the word order is often incorrect. Please remember that we taught the model only character sequences, not word sequences. Clearly, we would not accept a similar answer from a real world LLM. Nevertheless, I hope you accept the result as a general proof that the transformer architecture like implemented in our toy project works in principle.
We can also give a more meaningful context than just a 2d-tensor with one 0 in it. To do so, we first encode the context sentence, transform it into a PyTorch tensor and input the context tensor to the model.generate() method.
# Encode a starting sentence
text = [["The king was very sad and tired"]]
context = encode(text, ctoi)
# Transform context to PyTorch tensor
context_tensor = torch.tensor([context], dtype=torch.long, device=device)
# Generate new text in response to context sentence
print(decode(model.generate(context_tensor[:,0,:], max_new_tokens=500)[0].tolist(),itoc))

Conclusion
The transformer architecture, originally presented in “Attention Is All You Need”, sparked a rapid evolution of Large Language Models and other generative AI tools with fascinating performances. The evolution is far from over, and we see new and improved solutions emerging almost every month.
In part 1 of this article, we studied the logic and math behind the transformer model in depth. The core of the transformer is the attention mechanism, which captures the context in which words or tokens are used. Context is essential to correctly understand the meaning of words and sentences. The attention mechanism saves the recognized context through an adjustment of the word embedding vectors. These modified embedding vectors are further processed in fully connected neural networks to find the next token as the output of the LLM.
In part 2, we coded all steps of the transformer architecture in a toy project, the Fairy_Tale_GPT. The intention was to deepen the conceptual understanding and to demonstrate the theory in action. The example basically works, but at the same time, it illustrates how demanding human language is for computer models. In real applications, LLM model sizes exceed the trillion-parameters limit and are trained on terabytes of data.
I hope you gained a solid understanding of how Large Language Models work and enjoyed the journey. Let’s be curious about what comes next in this fascinating field of research!
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














