BLUPs and shrinkage in Mixed Models

Last Updated on January 6, 2023 by Editorial Team

Last Updated on February 27, 2022 by Editorial Team

Author(s): Dr. Marc Jacobs

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Data Visualization

Using SAS

Mixed Models are a great tool for estimating variance components and using those estimates to provide predictions. The predictions coming from Mixed Models are called Best Linear Unbiased Prediction(BLUP), and they are called that way because they include the fixed and random effects of the model to provide a prediction.

By including both fixed and random effects, Mixed Models allow a technique called ‘shrinkage’, or partial-pooling, which limits the potential for overfitting. In short, when a Mixed Model is made, the fixed effect is estimated across all observations, but the random part is done per level.

So, if you have observations across time for 100 people, you could ask the model to estimate different intercepts and different slopes (trajectories) for each of those 100 people. Now, you have multiple modeling options:

You fit a linear regression model on all the observations. This is called a pooled model since no people-level trajectories are estimated. Just one single intercept and one single slope.
You fit a linear regression model on each observation, separately. Now, you have estimated 100 intercepts and 100 slopes, separately, per person. This is the equivalent of splitting the dataset up in 100 parts. None of the people know the other 99 exist.
You fit a mixed model. The fixed intercept and slope effect are global, but you also estimate a person-dependent intercept and slope. To realize such feet, there needs to be enough variance in both the start and the trajectory of the curve. The way the random parts are estimated is called partial-pooling since the form follows a Normal distribution[0, variance]. Here, each specific random effect is determined by the population effect and person-specific deviance. To counter overfitting, the estimates furthest away from the population average are shrunk back the most to zero, since we believe they are more like anomalies. If we would not do so, the variance estimate of the random effect would explode.

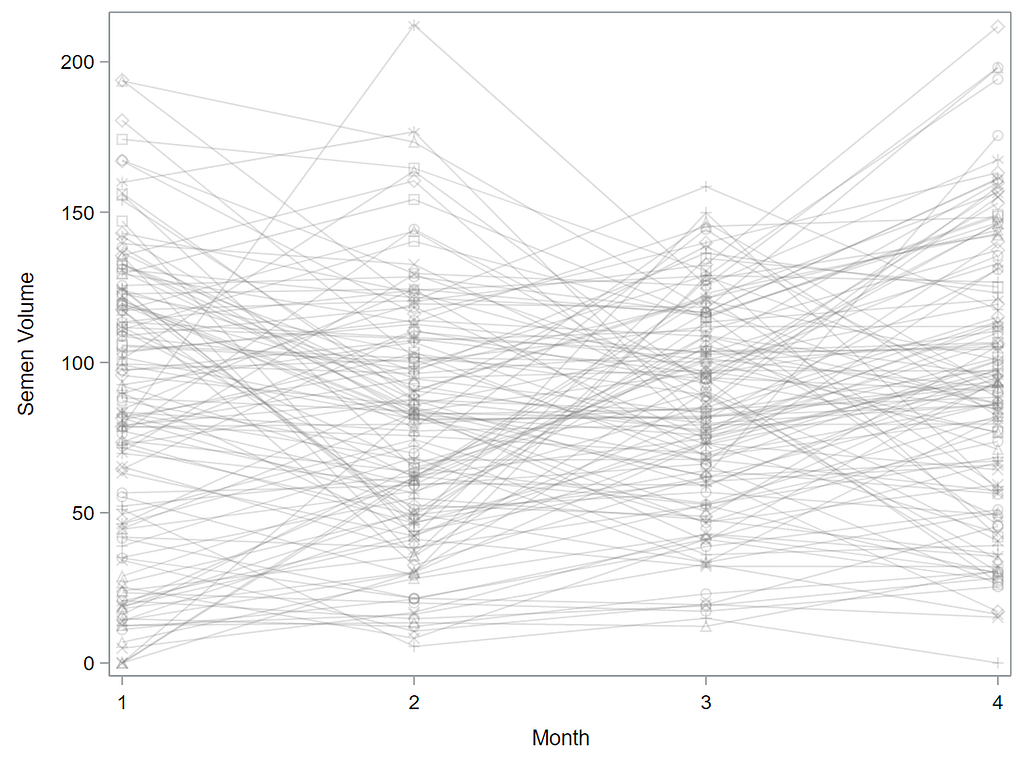
Now, in this example, using SAS, I will show you how I compared pooled, no-pooled, and various partially pooled models on a dataset containing the semen volume of 129 boars measured at 4 time points.

I am looking for sufficient variation to warrant estimating random effects.

The plots clearly show how the observations to the left are closely followed by the predictions. Such a model is dangerously close to overfitting, although standard statistics like R-squared will disagree. To these statistics, an un-pooled model will eagerly follow observations and thus fit very closely.

The pooled model makes a pooled estimate. To this model, the variation is just unexplained variation. You can expect the standard errors of the intercept, slope, and quadratic slope to have exploded.

The intercept and slope for sure hint at deviances from the population mean. The quadratic slope does not seem to shift that much at the boar level. Hence, this graph hints at a random-intercept-random-slope-model.

The intercept model seems to show a high fluctuation across the population mean in both the un-pooled and the mixed model. The mixed model does not really recognize variance in the slope, which in contrast with the un-pooled model. In general, a mixed model is way more sophisticated tool to pick up any necessity for a random component.

Global Fixed and Random effects for each of the five types of models. As you can see, the last model would not converge. No statistical tests for random effects should be used. Instead use graphs, like below.

The graph to the left shows what each model brings to the tabel. Although they tend to predict well, overall, their limits differ substantially based on what was included. The low confidence and prediction limits of the pooled model are paradoxical unless you realize that the mode were asked to estimate population means. The pooled model is made for that. To the right, you can clearly see how each model ‘thinks’. The un-pooled model provided boar-specific fixed estimates, whereas the pooled model only provides a global estimate. The random-intercept and random-intercept-month both provide shrunk predictions. It can be clearly seen that they do not fall for the extreme observations. Hence, limiting overfitting by shrinkage.

Boar-specific estimates coming from the un-pooled and mixed models. The graphs are a bit difficult to compare due to changing axes, but they depict the same data showing a substantial amount of variation at the intercept, but less at the slope. They also show the shrinkage applied at the boar-specific intercepts — confidence limits are much smaller in the mixed model than in the un-pooled model.

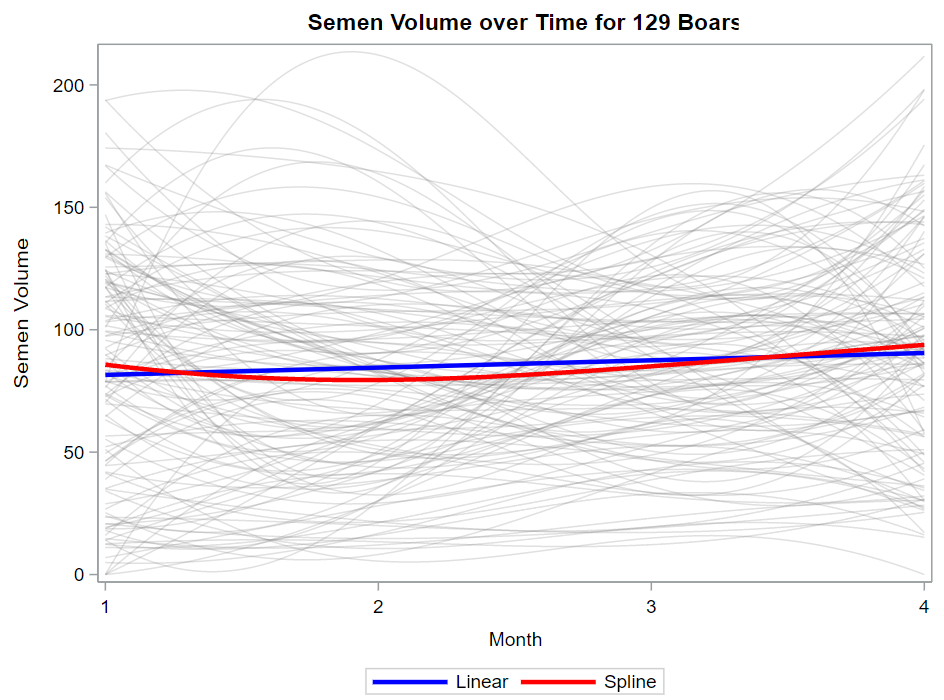
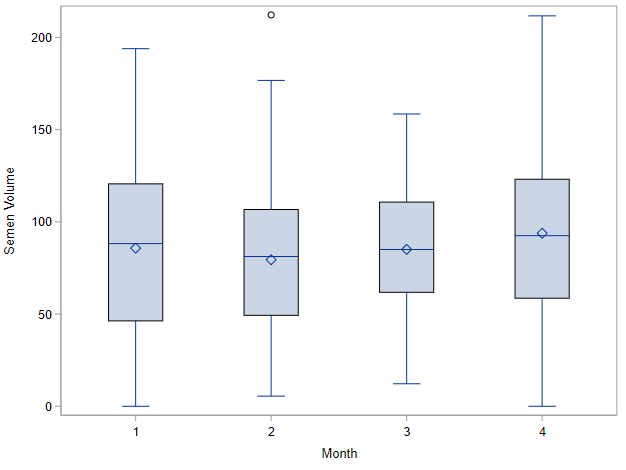
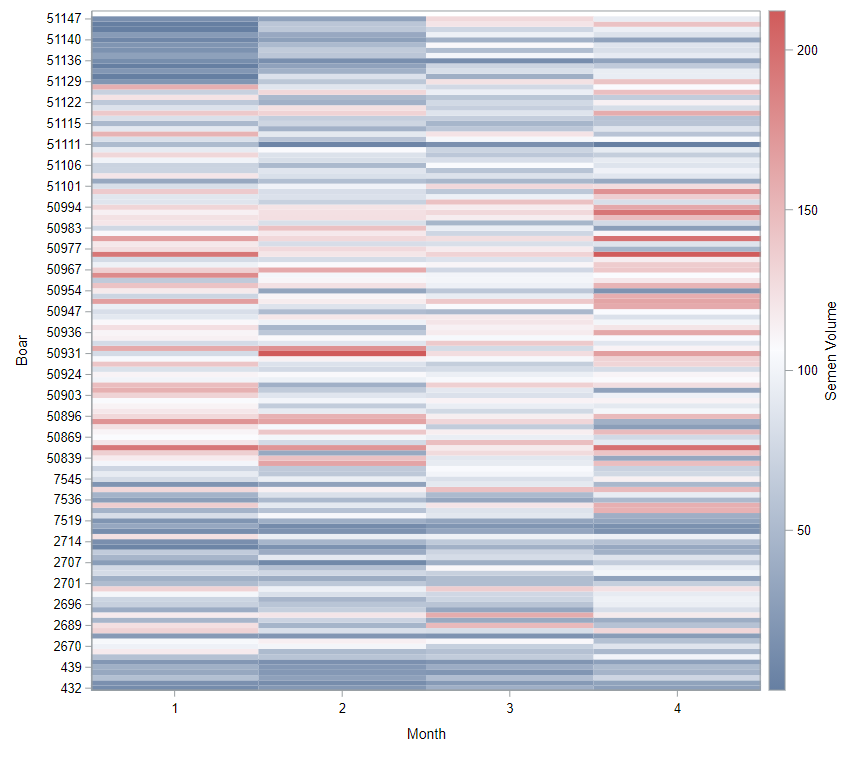
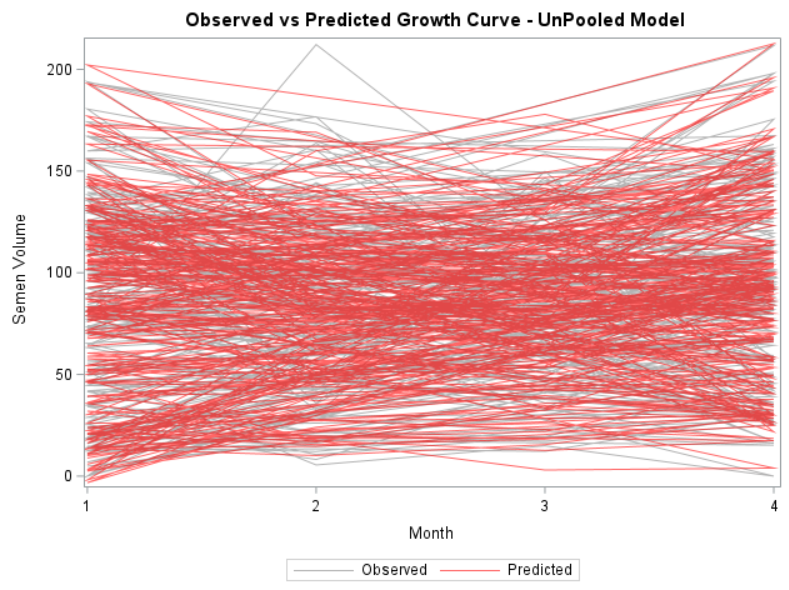
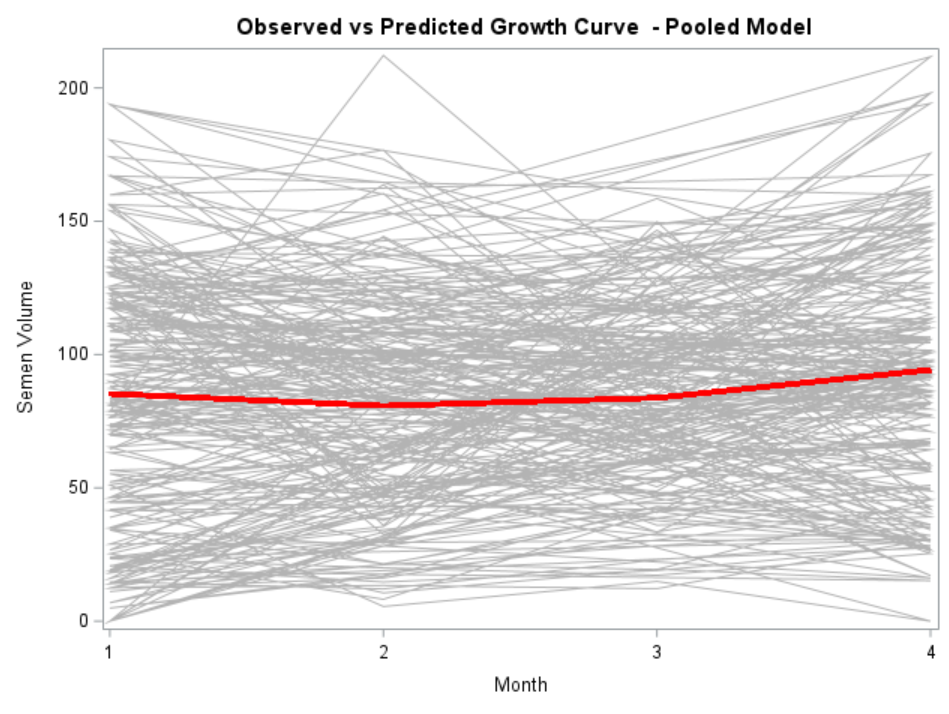
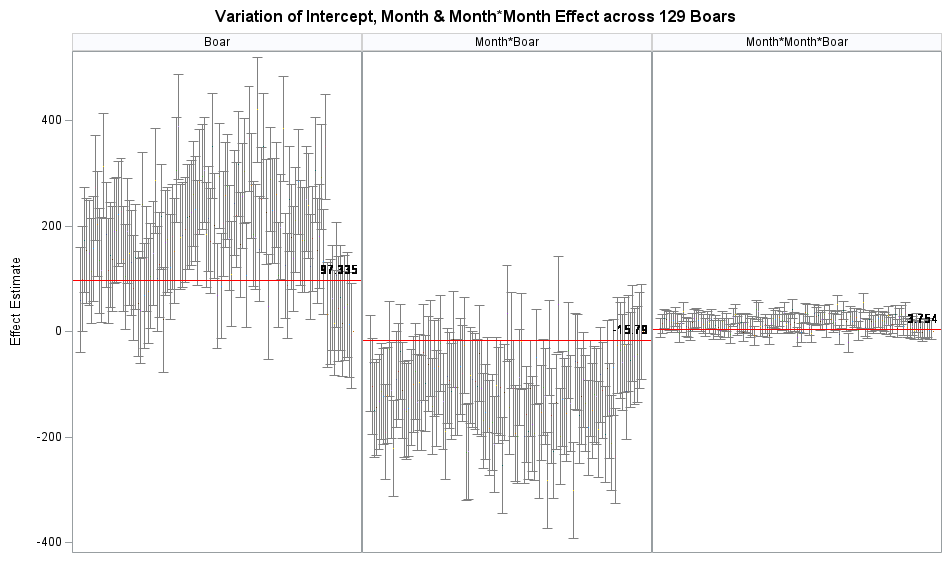
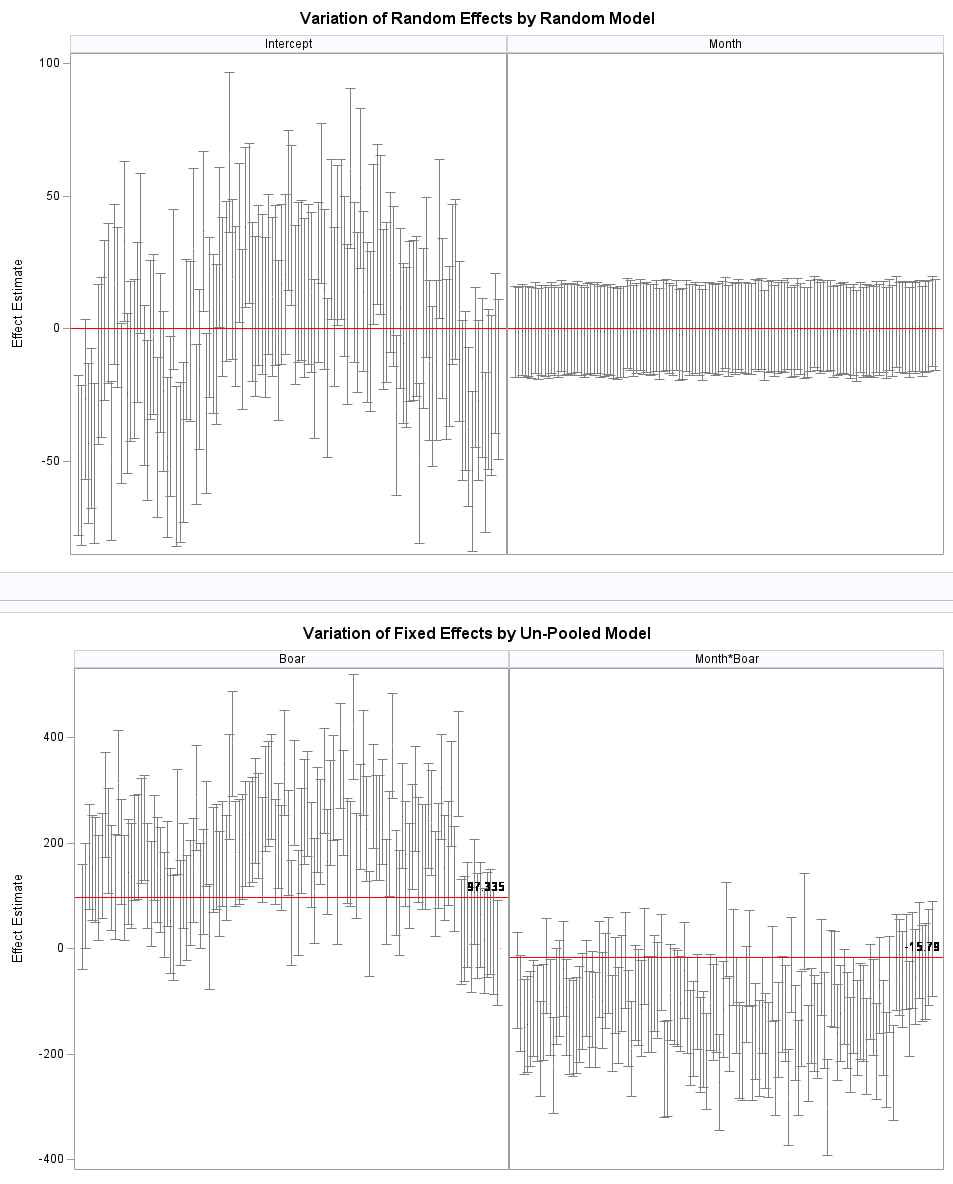
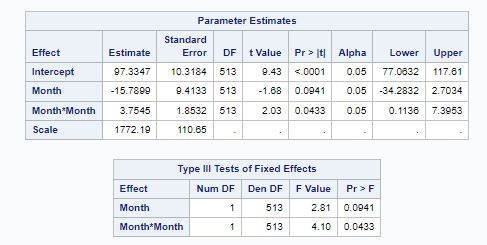
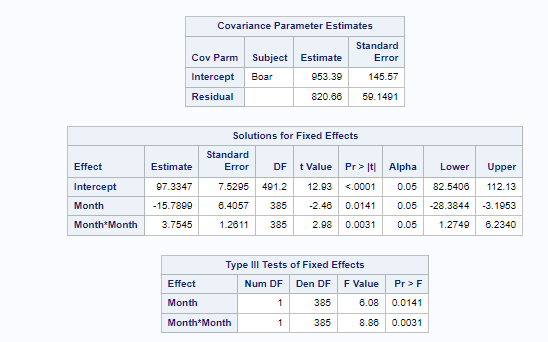
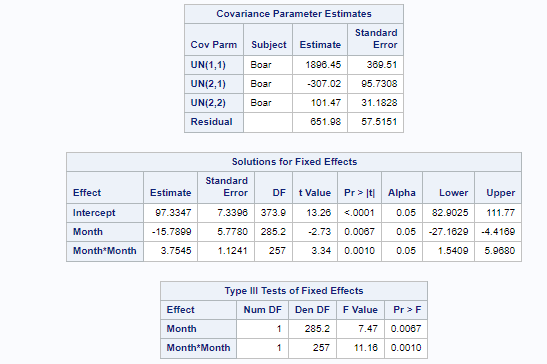
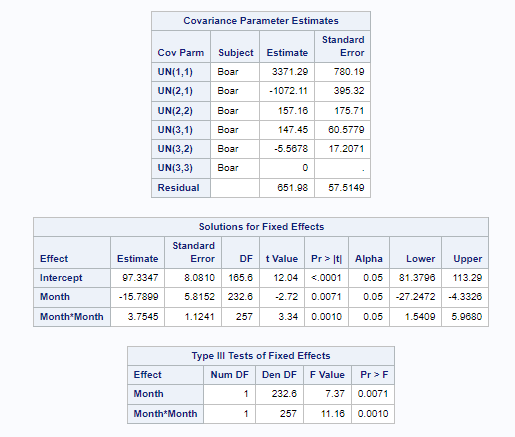
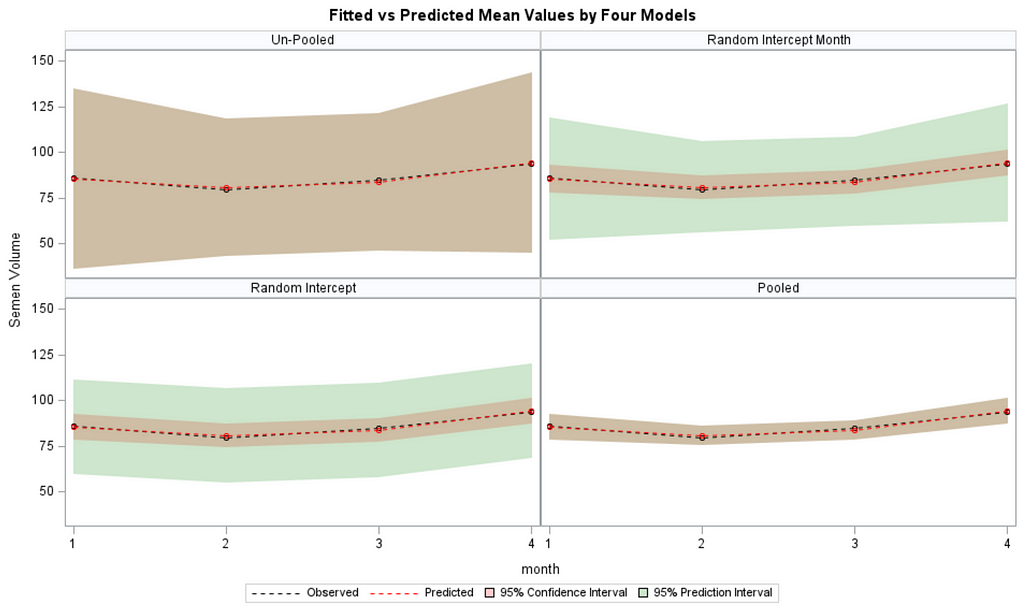
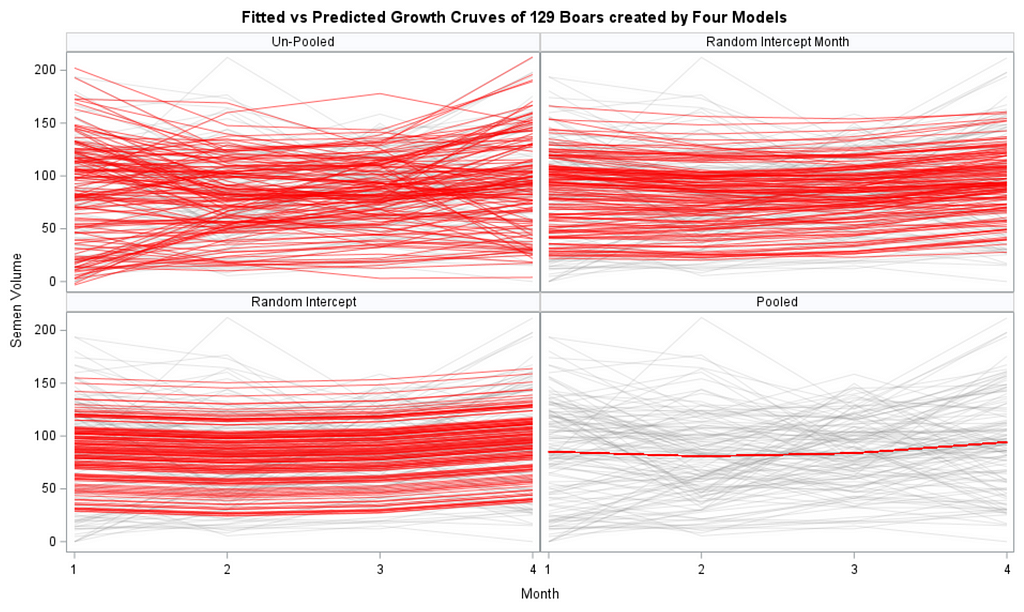
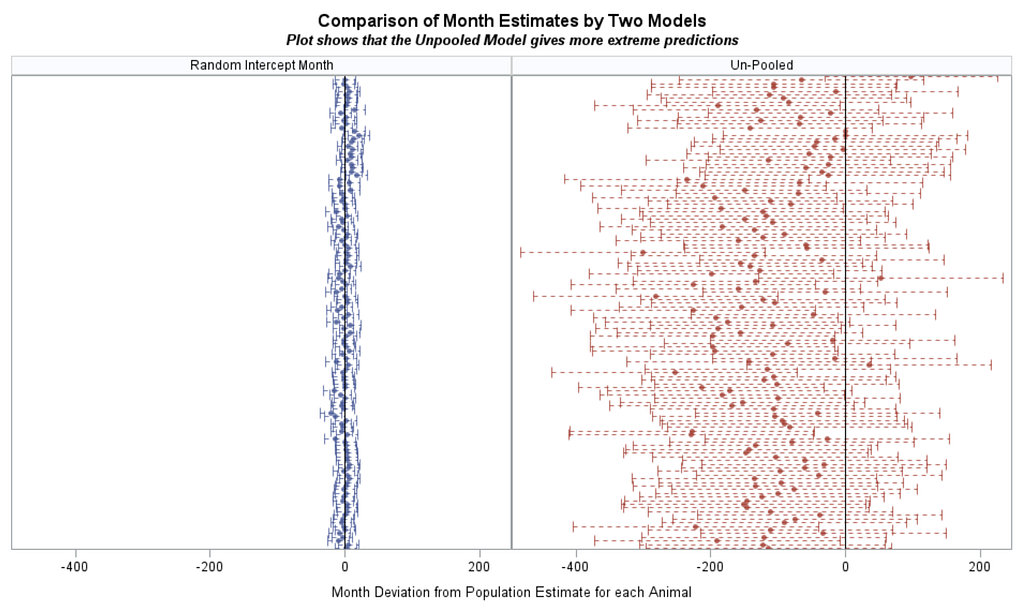
Below you can see some additional pieces of code added to look deeper into specific Mixed Models created. They are not easy to use and often lead to non-convergence or matrices that are not positive definitive. If such a warning should arise, you need to simplify the model.

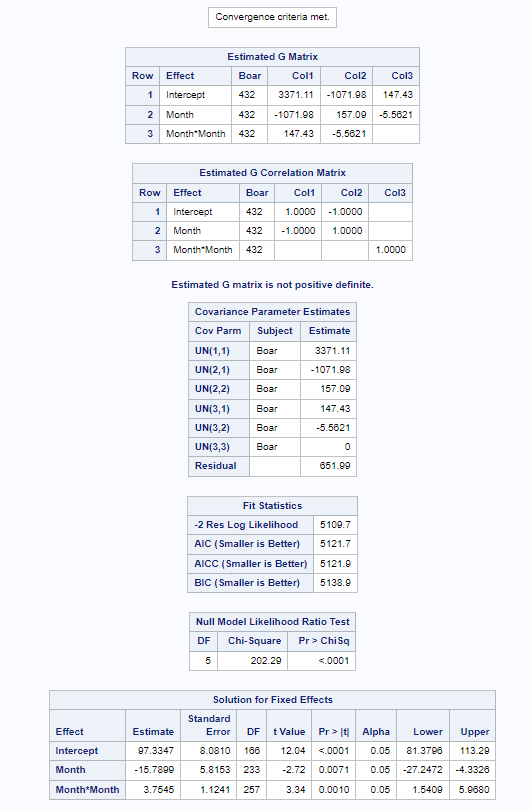
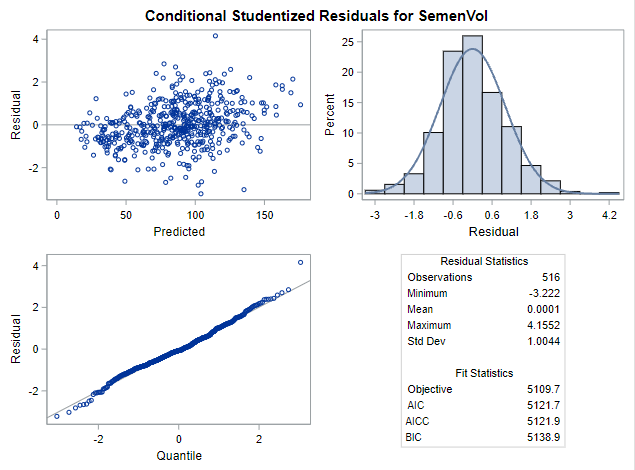
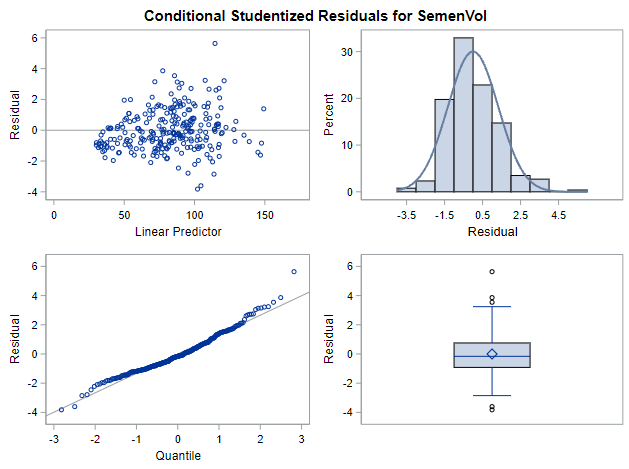
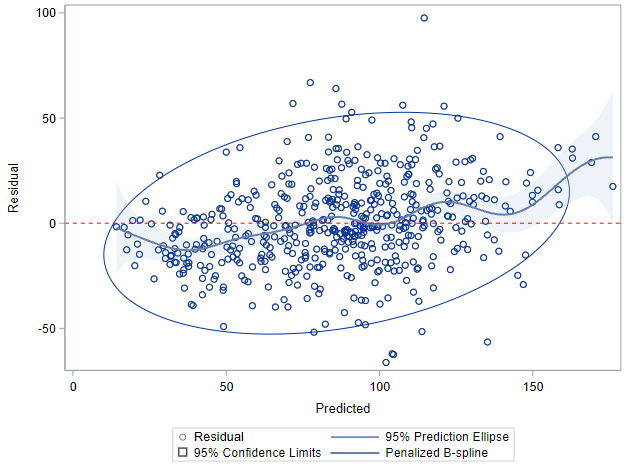
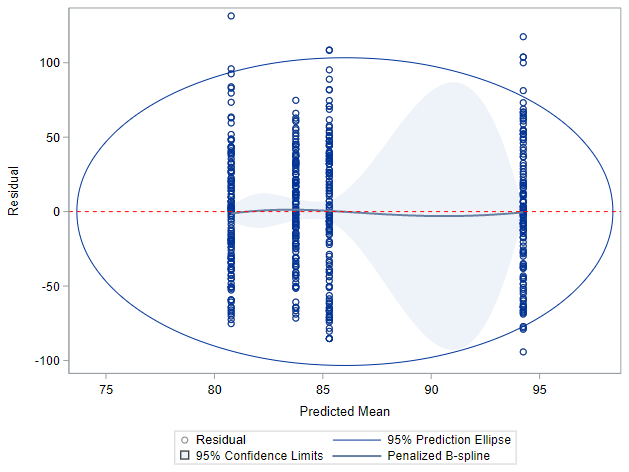
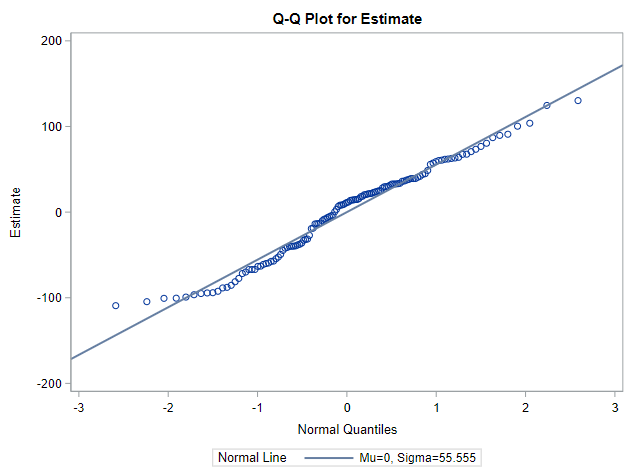
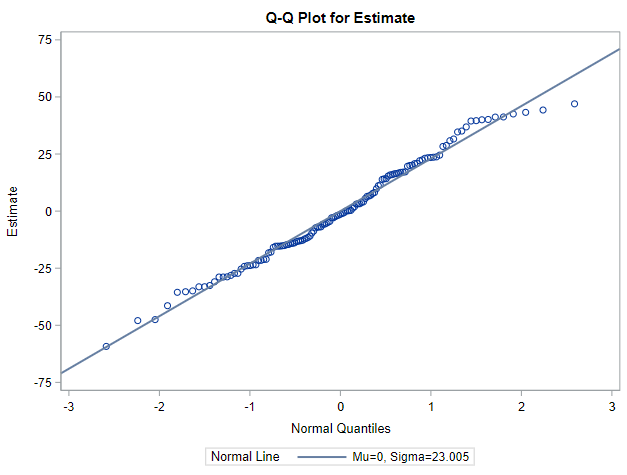
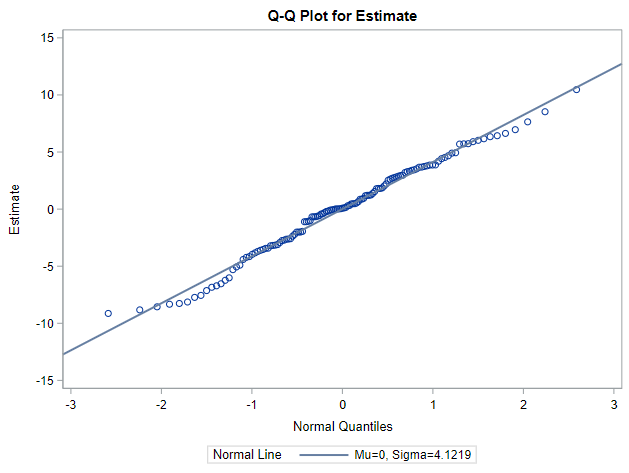
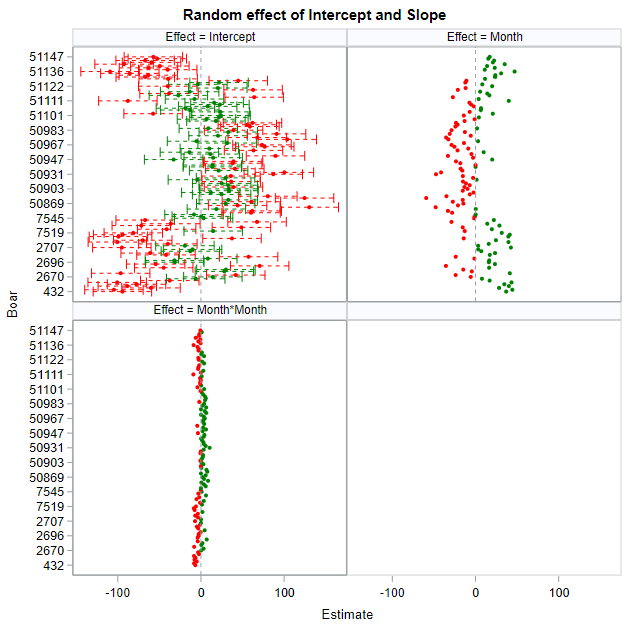
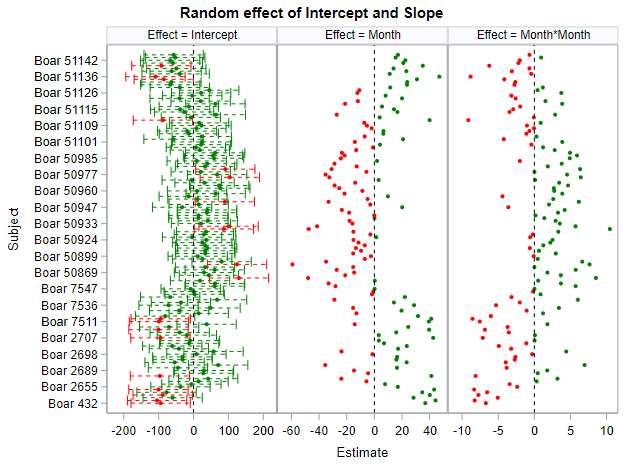
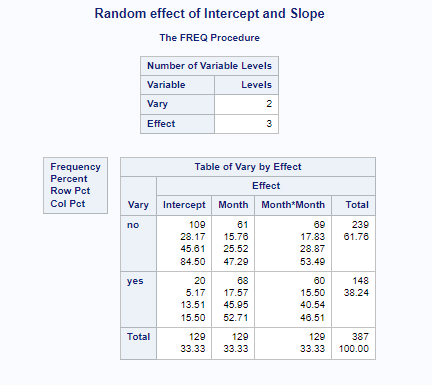
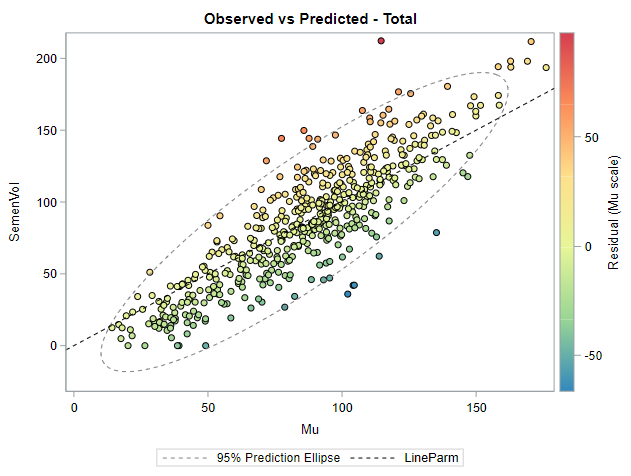
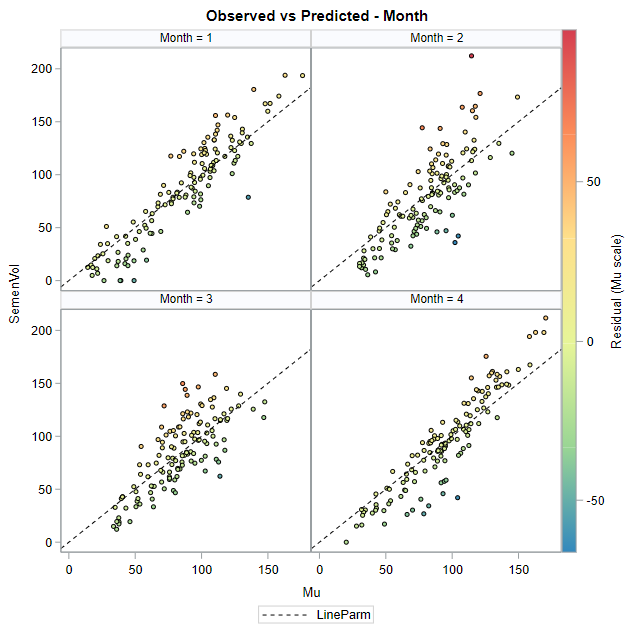
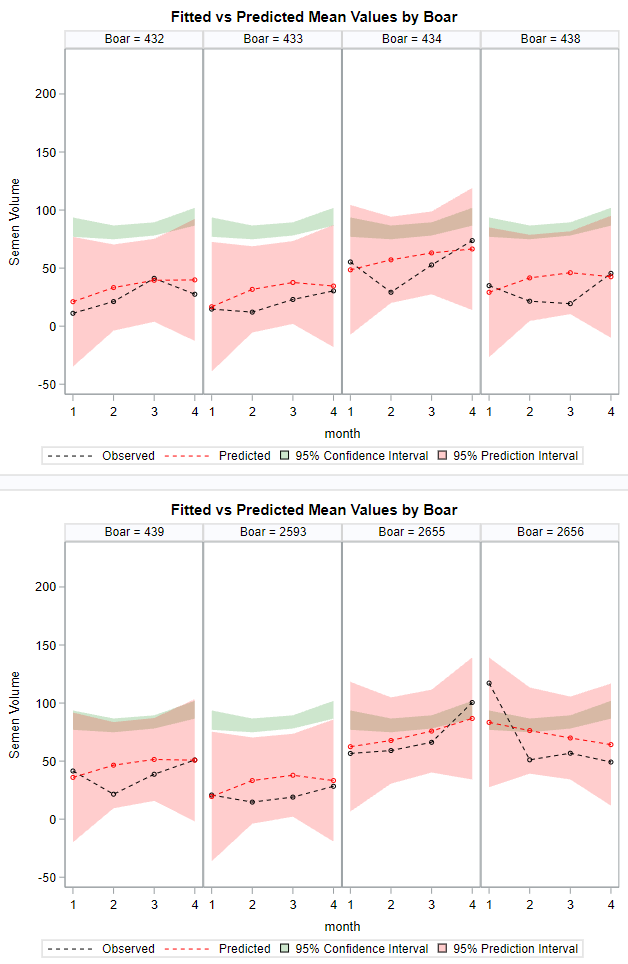
These plots show if the normality assumption of the random effects is met, where it makes sense to include a random effect, and how often estimates within a random effect vary. The latter part will give you a nice hint at the level of shrinkage applied.

I always like to look at the predictions provided by a mixed model for each of the levels included in the dataset — here, this would be: total, month, animal. As you can see in the animal-level predictions, the marginal prediction (green line) is no good.

I hope this post gave you a bit more feeling about what BLUPs are and shrinkage does. Please reach out to me if you have questions, ideas, or just want to spar!

BLUPs and shrinkage in Mixed Models — SAS was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI

Frequently Used, Contextual References

Resources

Publication

BLUPs and shrinkage in Mixed Models — SAS

Author(s): Dr. Marc Jacobs

Data Visualization