A Discourse on Reinforcement Learning

Last Updated on July 7, 2021 by Editorial Team

Author(s): Yalda Zadeh

Artificial Intelligence

Part I — AN EXPANSIVE SETTING

Co-author(s) | Sukrit Shashi Shankar

The narrative presents an expansive setting, with multiple paradigms, related around the theme of Reinforcement Learning(RL). We believe that such a setting may help the reader to perceive a broader view of RL, realizing its underlying assumptions, and foreseeing unexplored links for further research.

This is the first of the 3-article series “A Discourse on Reinforcement Learning”; We start here with a holistic overview of RL with an expansive setting.

✔️ Part I — An Expansive Setting

◻️ Part II — Algorithmic Methods & Variants

◻️ Part III — Advanced Topics & Future Avenues

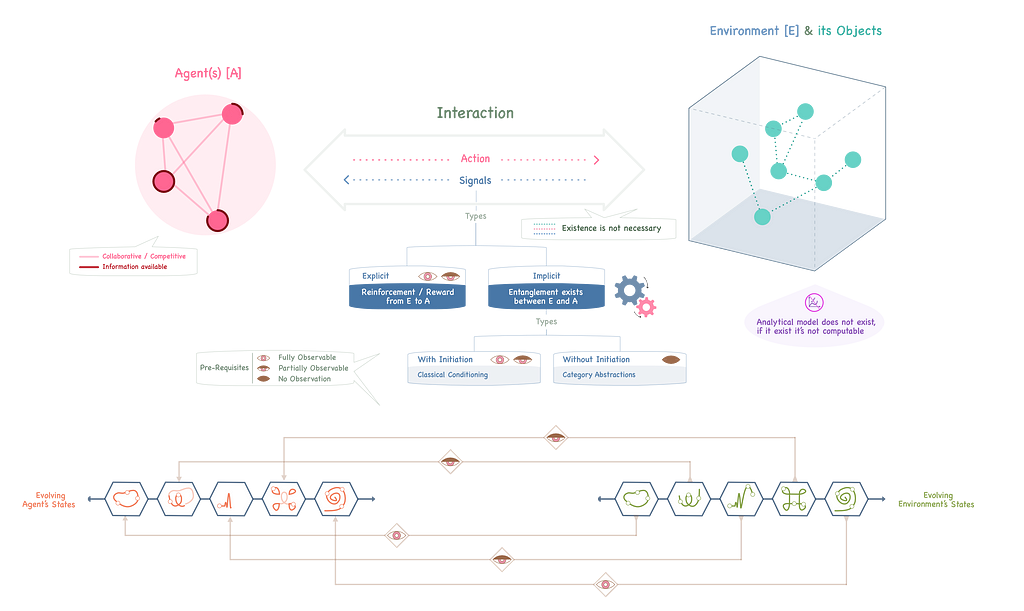
a. Agent(s) & Environment

Let us consider a general setting, where an agent (or a set of agents) and environment are usually two disjoint entities.

The role of the agent(s) is that of a learner, trying to achieve a sequential decision-making goal, by interacting with the environment. While in a single-agent setting, the mutual dynamics between the agents do not hold (since there is only one agent); in a multi-agent setting, the ☟[mutual-agents interplays] may well need to be considered.

[mutual-agents interplays] The agents may collaboratively, competitively, or under a mixed setting (a mix of collaboration and competition), strive to arrive at decisions. While doing so, agents may also sometimes suffer from imperfect information amongst themselves, i.e. what all one agent knows, the other agent may only partially or not know.
While we do not exclusively target multi-agent settings in this narrative, we are keen to provide intuitive portrayals at places, for a more consummate understanding.

The environment, on the other hand, may be seen as something, that potentially contains multiple objects, whose actions (or inactions), along with how the agent(s) interact with the environment, define the situation of the environment at a given instance of ☟[time].

[time] Note that since we are talking about sequential decision making, we can invoke the notion of time here. As we shall see later, the situations of the environment may be critical for the agents to make decisions.

The objects of the environment may or may not have any direct connection (or interaction) with the agents. For instance, it may be the case, that the agent(s) interact with only a subset of the objects, thereby influencing their future behaviour, and thus, affecting the environment.

For the agent(s), the situations of the environment can be:

▪ Fully Observable
▪ Partially Observable
▪ Unobservable

Based on the situation, presented (or not presented) to the agent(s), agent(s) make their decisions. These situations may be seen as states of the environment, and the decisions that the agent(s) take in response to the communication of such situations are their ☟[action(s)].

[action(s)] Note that the action taken by the agent(s) may just be that no action is taken, which is a very valid decision. Also, the actions may not necessarily be taken, immediately in response to observing the environmental states; rather, some actions may be dependent on the observation of past states, and more generically, even on the estimation of future states, that the environment may attain.

b. States

We mentioned above that the states of the environment roughly equate to the situations of the environment.

📎 Do we have the states of the agent(s) as well?
📎 Can we also have the states of the environment objects?
📎 What do these states tell us, or, when can we say that something is a state?

Let us carry forward this discussion from our notion of a situation. At any instance of time, a situation of the environment reflects what has happened in its past, due to objects’ behaviours, agent(s) interactions, initial situations the environment was in, etc. Therefore, in some way, the situation will also partly affect, how the future shapes up for the environment. Under this philosophy, a state of an entity can be anything, that contains its past, and thus, in some way, may affect its future 📄.

📄 [Reference] D. Silver, Google DeepMind 1, 1 (2015).

We can now relate, that the states of the agents(s) may be formed out of their past actions, observations, inputs and outputs owing to their interaction with the environment, etc. Similarly, the past history of internal behaviours, external inputs due to interactivity, outputs to the outside world, etc., may form the states of the objects.

💡 Remark - Note that the objects are considered to be a part of the environment. Thus, while the environment can be seen at the apex of its hierarchy, the objects, are at a lower level in the same hierarchy. The agent(s), however, being disjoint from the environment, sit at the top of a separate hierarchy. For the sake of simplicity, and ease of optimization (will be discussed in Part II), we would normally not talk about the states of the entities, which are not at the apex of any hierarchy.

Most texts while talking about the states of the environment would simply refer to them, as states. This is because, when the agent(s) can fully observe the states of the environment, they normally do not need to build their own states for decision-making (the environment’s state is their state). However, when the observation is partial or null (at some instance of time), the agent(s) would need to build their own states. For this, they may need to augment the part (or null) state communicated by the environment, with a piece of their own history of observations, actions, etc. to carry out subsequent/ future actions.

Unless explicitly specified, from now on, we would also refer states of the environment, simply as states.

c. Environment Functionality and States

The states of an environment reflect its functionality. Are states the only way, to know about the environment? Doesn’t it look like a slow process, something similar to taking snapshots of a time-sequence at regular intervals, and thereby un-charting it step-wise-step?

What if we could instead have a mathematical-physical model, of the environment’s evolution and functionalities? In other words, given some initial states (or conditions) of the environment, what if one could estimate the future states?

While the former provides a glimpse of model-free learning, the latter talks about having model-based learning. In specific terms, we can say,

▪ Model-Free Learning (MFL), implies that the agent(s) are not aware of any analytical model of the environment, but instead approximate it through the environmental states.
▪ Model-Based Learning (MBL), would instead require precise knowledge of a computable analytical model of the environment.

Most of our discussion here will hover around model-free learning since, in practical situations, it is often difficult to analytically describe an environment. However, we will cover the relevant concepts of model-based learning in Part III.

d. Environmental Stimuli

When the agent(s) observe the environmental states, they may be driven to take action(s). However, this requires that there exist some stimuli that the agent(s) should experience or receive from the environment. The types of environmental stimuli, depend upon the three possibilities of state-observation, viz. agent(s) fully observe the state, partially observe the state, or don’t observe the state at all.

If the agent(s) can’t observe the states, the only way to stimulate can be through some sort of ☟[entanglement] between the states of the environment and the agent(s). In layman terms, this may mean that the states exhibit some kind of energy, which can be felt by the agent(s) and can provide them with the stimuli to take the action(s).

[entanglement] One may normally relate this to some form of quantum entanglement; however, classical entanglement may also exist, if the states are lossy. Quantum entanglement may or may not exist when the systems are lossless, but classical entanglement can never exist for lossless systems 📄.
📄 [Reference] D. G. Danforth, “Classical entanglement,” in “arXiv preprint quant-ph/0112019,” (2001).

If the agent(s) fully or partially observe the states, there can be two options:

🔗 No entanglement between the states and the agent(s) exists; therefore, the environment needs to provide explicit stimuli (signals) to the agent(s) to help them decide upon their action(s).
🔗 Some type of entanglement between the states and the agent(s) exists, which gets initiated only when the agent(s) are able to observe at least a subset of states, and implicit stimuli are released.

In the field of psychology, the latter is better known as classical conditioning, while the former is termed operant conditioning. A typical example of classical conditioning is, if a person after seeing an ice cream (state of the environment), starts salivating (entangled action due to the implicit stimulus that activates the salivating glands) since he/ she likes it a lot. On the other hand, operant conditioning needs to supply explicit signals to the agent(s).

Under operant conditioning, the environment may provide signals to the agent(s), which can help them ameliorate/ improve their behaviour, or deteriorate their behaviour. Since we are interested in the agent(s) achieving their goals, we would normally want the agent(s) to improve their behaviour (through actions), and never deteriorate their behaviour towards something that takes them away from their goals. The improving-type signals are reinforcement for the agent(s), and the deteriorating-type signals are punishment.

The reinforcement signals (rewards) can be positive or negative, i.e. the environment can tell the agent(s) whether their action(s) are good or bad, if they have to achieve their goal(s). The agent(s) may then adapt accordingly, by learning which action(s) are not good in what situations (states) and which actions(s) are good.

🧬 The learning of the agent(s)is called Reinforcement Learning (RL) when,

+ An analytical (or analytically solvable) model of the environment is unknown,
+ There is no entanglement between the environment and the agent(s), either with or without initiation,
+The environment needs to reinforce the agent(s) through explicit signals/ rewards, such that the agent(s) progress to achieve their goal(s).

💡 Remark - Who designs the reinforcement signals? Is there something built-in within the environment, that can issue the reward signals? Well, under an entanglement setting, this might be possible, but under the reinforcement learning setting, it’s the user's (AI/ ML researcher's) job to specify the reward signals on behalf of the environment, such that the agent(s) always ameliorate their behaviour. 
Now while doing so, one may imagine that the user has some prior knowledge about the functionality of the environment. However, this knowledge is not in a comprehensively mathematically formulated manner, else the user could have designed an analytical model of the environment and supplied to the agent(s). 

e. Model-based Learning & Entanglement

What is the use of all this entanglement discussion, and why have we defined Reinforcement Learning above, under a model-free setting? Imagine that natural physical entanglement does not exist, and one then creates artificial entanglement. Isn’t this like model-based learning? Such confusions can be very obvious since most of the RL texts never talk about entanglement. However, we believe that there are clear distinctions, and it may be worthwhile to mention them here.

In the idealistic version of model-based learning, a mathematical model of the environment is known. The agent(s) should decide their action(s) using this model and no reinforcement signal is required to drive their actions.

In another variant of model-based learning, a mathematical model of the environment is neither provided, nor a rough estimation of the environment’s functionality is done through reinforcement; however, the analytical model of the environment itself is learnt. Here, the methods generally need some initial education, about which actions need to be applied for which states, and then a model (from a known family of mathematical models) is fitted to this experience.

In our view, in either of these variants of model-based learning (whether the model is known or analytically learnt), the abstraction differs from the typical RL setting, and we thus, generally consider RL as being model-free.

Let us take the example of Chess. Here, the rules of the game would define the environment’s model, and the agent (the player) needs to take action(s) to win against the opponent (the object situated in the environment, changing its states, besides the agent). What if the rules of the game could exist as a mathematical abstraction, the player’s actions as another mathematical abstraction, and a language that defines interaction (collaboration or collapse) between these two abstraction spaces? Dealing with such abstractive spaces is what we say, enables entanglement, though artificially.

One may argue that human-defined abstractions are nothing but mathematical structures, and thus, one has defined a mathematical model. However, there are three important differences between defining abstractive spaces for entanglement and mathematical model for typical model-based learning,

📎 the mathematically abstractive models are defined for both the environment and the agent, and not only for the environment,
📎 no explicit rules and action spaces are defined, but only their abstractions are analytically specified,
📎 interactivity rules between the two abstractive structures are also defined.

Although the notions around entanglement are highly unexplored, we introduce them here, since we would relate these to concepts from Category Theory in Part II, III for providing potential extensions to some RL elements.

---

A Discourse on Reinforcement Learning was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI