NLP, NN, Time series: Is it possible to Predict Oil Prices Using Data From Google Trends?

Author(s): Krikor Postalian-Yrausquin

Originally published on Towards AI.

Using Word2Vec first, then scraping from Google Trends for the frequency of Google searches, followed by time series (via a Fourier decomposition) and neural networks with Keras, I attempt to predict future oil prices.

In many publications, we see algorithms put in place to perform a specific task, but in reality, a complete data analytics/science work is a complex endeavor that will require a combination of different steps, each one with a core analytics task and model, in order to get useful results.

This project is a very ambitious attempt to predict gas prices based on three algorithms: NLP (word2vec) to find words related to ‘Oil’, time series decomposition after Fourier analysis (to predict each time effect separately), and neural networks with Keras to predict, using the frequency of word searches in Google, the random variation of the oil price.

This is in a high level the structure of the approach followed in this work:

The first step is to load the necessary libraries and download the pretrained NLP models from Gensim. I used two Word2Vec models, one trained with Wikipedia data and the other with Twitter data.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.tsa.seasonal import MSTL
import klib
from scipy import spatial
import gensim.downloader as api
from statsmodels.tsa.seasonal import MSTL
from nltk.stem import WordNetLemmatizer
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from datetime import timedelta
import tensorflow as tf
import math
import nltk
from scipy import optimize
from sklearn.preprocessing import MinMaxScaler
nltk.download('wordnet')
from pmdarima import auto_arima

model1 = api.load("glove-wiki-gigaword-200")
model2 = api.load("glove-twitter-100")

Word2Vec is the right choice for the NLP portion of the analysis because:

1. It is trained to be used for similarities-distances, unlike BERT, for example, which is usually trained for different downstream tasks, like masking.
2. It generates word embeddings, which is what we are trying to obtain and compare.

In this case, I justify the use of a pretrained model since we are going to use this over Google data, which is supposed to be clean. In works where the text data is not clean, or the used language is too specific, I wouldn’t recommend the use of pretrained models.

I am then defining a function to get the most similar words from both models and average them out.

def close_words(wrd):
 tbl1 = pd.DataFrame(model1.most_similar(wrd, topn=10), columns=['word','siml']).set_index('word')
 tbl2 = pd.DataFrame(model2.most_similar(wrd, topn=10), columns=['word','siml']).set_index('word')
 tbl = pd.concat((tbl1, tbl2), axis=1).mean(axis=1)
 tbl = pd.DataFrame(tbl).sort_values(0, ascending=False)
 return tbl

dfs = []

Here, I do a search on several keywords I think are related to oil or oil prices. First, I start with the word oil, then I look for other words that come from the list, following a “chain”. The step after this one “saves” the search results to a list of data frames.

At the same time, to avoid using similar terms, I apply Lemmatization. Note that prefer Lemmatization over stemming since the lemmas are real words that will appear in Google searches, the stems aren’t.

search = 'barrels'
wordsim = close_words(search)

lemmatizer = WordNetLemmatizer()
wordsim['Lemma'] = wordsim.index
wordsim['Lemma'] = wordsim['Lemma'].apply(lambda x: lemmatizer.lemmatize(x))
wordsim

If I like the results (they make sense to me), I add them to the list. Then, I repeat the process until I have a decent size list. Note that in this exercise, I have the limitation that the API I use to run against Google Trends has a limit on its free license.

Finally, I save the results to a file I can use in the scrapper.

dfs.append(wordsim)

finaldf = pd.concat(dfs, ignore_index=True).groupby('Lemma').mean()
finaldf.to_csv("finaldf.csv")

Now I save it all to a list, which I am going to use to search in Google Trends using a third-party API called Google Trends Scraper (https://apify.com/emastra/google-trends-scraper)

Disclaimer: This article is only for educational purposes. We do not encourage anyone to scrape websites, especially those web properties that may have terms and conditions against such actions.

The scrapper might take a while to run. Once the scraper is done, I save the results and import them. They are in a transposed format, so I account for that next and five the time series their format, same with the numbers.

workdf = pd.read_csv("dataset_google-trends-scraper_2023-10-17_07-39-06-381.csv")
workdf = workdf.T
df2 = workdf.iloc[[-1]]
workdf = workdf[:-1]
workdf.columns = list(df2.values[0])
workdf['Timestamp'] = workdf.index
workdf['Timestamp'] = pd.to_datetime(workdf['Timestamp'], format='%b %d, %Y')
workdf = workdf.sort_values('Timestamp')
workdf = workdf.set_index('Timestamp')
workdf = workdf.apply(pd.to_numeric, errors='coerce', axis=1)
workdf

I found that the predictors also have some seasonality in them, so I decompose them using a schedule of 52 and 104 weeks (one and two years). I use the residuals after the decomposition.

One certain improvement to this whole work could be using the same approach that follows for the response variable on the predictors, which in the interest of time, I did not do in this case.

a = []
for col in workdf.columns:
 sea = MSTL(workdf[col], periods=(52, 104)).fit()
 res = pd.DataFrame(sea.resid)
 res.columns = [col]
 a.append(res)

xres = pd.concat(a, axis=1)
xres

The next section of this work deals with the preparation of the response variable.

First, I import the gas prices from government data and apply format to them as well.

ydf = pd.read_csv("GASREGW.csv")
from datetime import timedelta
ydf['DATE'] = pd.to_datetime(ydf['DATE'], format='%Y-%m-%d') - timedelta(days=1)
ydf = ydf.sort_values('DATE')
ydf = ydf.set_index('DATE')
ydf = ydf.apply(pd.to_numeric, errors='coerce', axis=1)
ydf

Now, I want to explore more about the seasonality of oil prices. In order to do that, I do a Fourier transform on the series to find the frequency, of which the inverse will be the time period (in weeks) of the possible components.

I then extract those components with higher amplitude and use those as the input for the seasonal decomposition.

from scipy.fft import fft, fftfreq
import numpy as np
yf = fft(ydf['GASREGW'].values)
N = len(ydf)
xf = 1/(fftfreq(N, d=1.0))
nyf = np.abs(yf)
four = pd.DataFrame({'Period':xf, 'Amp':nyf})
four = four[(four['Period']>0) & (four['Period']<=200)]
four = four.sort_values(['Period'], ascending=True)
four['Period'] = four['Period'].apply(lambda x: math.floor(x))
four = four.groupby('Period').max().reset_index(drop=False)
four = four.sort_values('Amp', ascending=False).head(5)
four

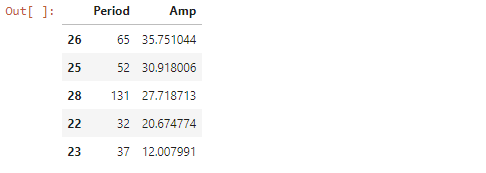
Next, I do the time-series decomposition. Note that I replaced 131 weeks with 104 weeks since I can’t go further with the data I have.

The results are very nice, I believe, for several reasons:

1. The trend is linear.
2. The seasonalities have a regular sinusoidal behavior.
3. The residual looks “random”, which means all trending and cyclic behavior has been excluded from it.

What I am going to predict with Neural Networks is the residual.

seas = MSTL(ydf['GASREGW'], periods=(32, 37, 52, 65, 104)).fit()
seas.plot()
plt.tight_layout()
plt.show()

Now, I have nicely formatted the dataset I am going to begin with.

ydf['seasonal_32'] = seas.seasonal['seasonal_32']
ydf['seasonal_37'] = seas.seasonal['seasonal_37']
ydf['seasonal_52'] = seas.seasonal['seasonal_52']
ydf['seasonal_65'] = seas.seasonal['seasonal_65']
ydf['seasonal_104'] = seas.seasonal['seasonal_104']
ydf['Trend'] = seas.trend
ydf['Resid'] = seas.resid
ydf['Diff'] = ydf['Resid'].diff(-1)
ydf

The data is still not ready to model, first I need to renormalize to ensure that all the predictors are on the same scale.

def properscaler(simio):
 scaler = StandardScaler()
 resultsWordstrans = scaler.fit_transform(simio)
 resultsWordstrans = pd.DataFrame(resultsWordstrans)
 resultsWordstrans.index = simio.index
 resultsWordstrans.columns = simio.columns
 return resultsWordstrans

xresidualsS = properscaler(xres)
xresidualsS

Then, in order to “smooth” the residual, I will work on the derivative. Using the definition of derivative, and since the time period is constant, that just means working with the difference between residuals.

In this same step, I apply a Tanh transformation to the response variable. The reason I do that is because that is going to be my last activation function, and I want the real values and the predicted by the NN model to be in the same scale and range.

DF = pd.merge(xresidualsS, ydf, left_index=True, right_index=True)
DF['Diff'] = DF['Diff'].apply(lambda x: math.tanh(x))
DF.index = workdf.index
DF = DF.dropna()
DFf = DF.drop(columns=['GASREGW','seasonal_32','seasonal_37','seasonal_52','seasonal_65','seasonal_104','Trend','Resid'])
DFf

Since descriptive analytics is not the goal of this work, and this document is already long, I am just going to do a quick exploration in the form of a correlation matrix.

corr = DFf.corr(method = 'pearson')
sns.heatmap(corr, cmap=sns.color_palette("vlag", as_cmap=True))

Finally, it is time to go to the modeling stage. As usual, the first step is to split the data into training and evaluation sets.

finaleval=DFf[-12:]
subset=DFf[:-12]

x_subset = subset.drop(columns=["Diff"]).to_numpy()
y_subset = subset['Diff'].to_numpy()
x_finaleval = finaleval.drop(columns=["Diff"]).to_numpy()
y_finaleval = finaleval[['Diff']].to_numpy()

Then I use a Neural Network regression strategy from the Keras library. As mentioned before, the activation function I use is Tanh, which I found was the best for this exercise after trial and error.

#initialize
neur = tf.keras.models.Sequential()
#layers
neur.add(tf.keras.layers.Dense(units=1000, activation='tanh'))
neur.add(tf.keras.layers.Dense(units=5000, activation='tanh'))
neur.add(tf.keras.layers.Dense(units=7000, activation='tanh'))

#output layer
neur.add(tf.keras.layers.Dense(units=1))

from keras import backend as K
def custom_metric(y_true, y_pred):
 SS_res = K.sum(K.square( y_true-y_pred ))
 SS_tot = K.sum(K.square( y_true - K.mean(y_true) ) )
 return ( 1 - SS_res/(SS_tot + K.epsilon()) )

#using mse for regression. Simple and clear
neur.compile(optimizer='Adam', loss='mean_squared_error', metrics=[custom_metric])

#train
neur.fit(x_subset, y_subset, batch_size=220, epochs=2000)

There we go. We have a model. I now evaluate the unseen data. The R2 is not too bad, not the best, but not bad.

test_out = neur.predict(x_finaleval)
output = finaleval[['Diff']]
output['predicted'] = test_out
output['actual'] = y_finaleval
from sklearn.metrics import mean_absolute_error, mean_squared_error, r2_score
print("R2: ", r2_score(output['actual'], output['predicted']))
print("MeanSqError: ",np.sqrt(mean_squared_error(output['actual'], output['predicted'])))
print("MeanAbsError: ", mean_absolute_error(output['actual'],output['predicted']))
output = output[['predicted','actual']]
output

Note that what was just predicted is the Tanh of the difference of the residuals. The next step is to undo these transformations.

output = output[['predicted']]
output['predictedArcTanh'] = output['predicted'].apply(lambda x: math.atanh(x))

output['PredResid'] = np.nan

start = 0
prevval = 0
for index, row in output.iterrows():
 if start == 0:
 prevval = -0.037122 - row['predictedArcTanh']
 else:
 prevval = prevval - row['predictedArcTanh']
 output.at[index, 'PredResid'] = prevval

output = output[['PredResid']]
output

Which is then our prediction of the residuals for those weeks.

We are not done yet, for the trend component of the decomposition, I will fit linear regression and extrapolate.

ydf['rown'] = range(len(ydf))
setreg = ydf[ydf.index <'2023-07-23']
setreg = setreg[['Trend','rown']]
mod = LinearRegression().fit(setreg[['rown']], setreg['Trend'])
setreg['PredTrend'] = mod.predict(setreg[['rown']])
plt.scatter(setreg['rown'], setreg['Trend'], color="black")
plt.plot(setreg['rown'], setreg['PredTrend'], color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

And these are my predictions for the trend.

outcome = ydf[ydf.index >='2023-07-23']
outcome = outcome[['GASREGW','rown']]
outcome['PredTrend'] = mod.predict(outcome[['rown']])
outcome

For the seasonal values, I fit them to a cosine function by creating a custom numpy function with the model I want to fit and giving it “good” seeds for the parameters (amplitude, frequency, fase angle, and offset). I had to run it several times since the results were very sensible for the seeds. This is predicting seasonal_32.

from scipy import optimize
from sklearn.preprocessing import MinMaxScaler
setreg = ydf[ydf.index <'2023-07-23']
setreg = setreg[['seasonal_32','rown']]
def fit_func(x, a, b, c, d):
 return a*np.cos(b*x+c) + d
params, params_covariance = optimize.curve_fit(fit_func, setreg['rown'], setreg['seasonal_32'], p0=(10,.19,0,0))

setreg['Predseasonal_32'] = setreg['rown'].apply(lambda x: fit_func(x, *params))
plt.scatter(setreg['rown'], setreg['seasonal_32'], color="black")
plt.plot(setreg['rown'], setreg['Predseasonal_32'], color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

The fit looks accurate enough. I’ll save the results in my outcome dataset.

#assign to outcome
outcome['Predseasonal_32'] = outcome['rown'].apply(lambda x: fit_func(x, *params))

I proceed the same way for the other seasonal components.

• Seasonal 37 weeks

setreg = ydf[ydf.index <'2023-07-23']
setreg = setreg[['seasonal_37','rown']]
def fit_func(x, a, b, c, d):
 return a*np.cos(b*x+c) + d
params, params_covariance = optimize.curve_fit(fit_func, setreg['rown'], setreg['seasonal_37'], p0=(10,.17,0,0))

setreg['Predseasonal_37'] = setreg['rown'].apply(lambda x: fit_func(x, *params))
plt.scatter(setreg['rown'], setreg['seasonal_37'], color="black")
plt.plot(setreg['rown'], setreg['Predseasonal_37'], color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

#assign to outcome
outcome['Predseasonal_37'] = outcome['rown'].apply(lambda x: fit_func(x, *params))

• Seasonal 52 weeks

from scipy import optimize
from sklearn.preprocessing import MinMaxScaler
setreg = ydf[ydf.index <'2023-07-23']
setreg = setreg[['seasonal_52','rown']]
def fit_func(x, a, b, c, d):
 return a*np.cos(b*x+c) + d
params, params_covariance = optimize.curve_fit(fit_func, setreg['rown'], setreg['seasonal_52'], p0=(10,.13,0,0))

setreg['Predseasonal_52'] = setreg['rown'].apply(lambda x: fit_func(x, *params))
plt.scatter(setreg['rown'], setreg['seasonal_52'], color="black")
plt.plot(setreg['rown'], setreg['Predseasonal_52'], color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

#assign to outcome
outcome['Predseasonal_52'] = outcome['rown'].apply(lambda x: fit_func(x, *params))

• Seasonal 65 weeks

setreg = ydf[ydf.index <'2023-07-23']
setreg = setreg[['seasonal_65','rown']]
def fit_func(x, a, b, c, d):
 return a*np.cos(b*x+c) + d
params, params_covariance = optimize.curve_fit(fit_func, setreg['rown'], setreg['seasonal_65'], p0=(10,.1,0,0))

setreg['Predseasonal_65'] = setreg['rown'].apply(lambda x: fit_func(x, *params))
plt.scatter(setreg['rown'], setreg['seasonal_65'], color="black")
plt.plot(setreg['rown'], setreg['Predseasonal_65'], color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

#assign to outcome
outcome['Predseasonal_65'] = outcome['rown'].apply(lambda x: fit_func(x, *params))

• Seasonal 104 weeks

setreg = ydf[ydf.index <'2023-07-23']
setreg = setreg[['seasonal_104','rown']]
def fit_func(x, a, b, c, d):
 return a*np.cos(b*x+c) + d
params, params_covariance = optimize.curve_fit(fit_func, setreg['rown'], setreg['seasonal_104'], p0=(10,.05,0,0))

setreg['Predseasonal_104'] = setreg['rown'].apply(lambda x: fit_func(x, *params))
plt.scatter(setreg['rown'], setreg['seasonal_104'], color="black")
plt.plot(setreg['rown'], setreg['Predseasonal_104'], color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

Finally, this is how the whole outcome dataset looks like:

#assign to outcome
outcome['Predseasonal_104'] = outcome['rown'].apply(lambda x: fit_func(x, *params))
outcome

The sum of all components will give me a predicted price.

final = pd.merge(outcome,output,left_index=True,right_index=True)
final['GASREGW_prep'] = final['PredTrend'] + final['Predseasonal_32'] + final['Predseasonal_37'] + final['Predseasonal_52'] + final['Predseasonal_65'] + final['Predseasonal_104'] + final['PredResid']
final

And, let’s see how we did!

sns.lineplot(x='index', y='value', hue='variable', data=pd.melt(final[['GASREGW','GASREGW_prep']].reset_index(drop=False), ['index']))
plt.ylim(3,4.5)

Which is very conservative in the price variation, but the model does get a general trend.

I guess that if I could predict the oil prices using free Google Collab Notebooks, I wouldn’t be here writing this whole project for you. But the reality is that there is some predictive power in the Google trend search topics that could be explored with more powerful tools.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI