Bayesian Updating and the “Picture Becomes Clearer” Analogy

Last Updated on November 16, 2020 by Editorial Team

Bayesian updating — revising an estimate when new information is available — is a key concept in data science. It seems intuitively obvious that (within an accurate probability model of a real-world phenomenon) the revised estimate will typically be better. One simple and correct mathematical formulation of “better” is that the revision can only decrease the mean squared error of the estimate.

But there is a subtlety, seldom pointed out in textbooks, which is that the actual error, while often decreasing, typically does not decrease at every “new information” step. That is, the “picture always becomes clearer” analogy is misleading.

I will discuss this in the context of estimating the probability that a specified event will occur before a specified date. Suppose an expert first assesses the probability as 50%, then later at 60%, then later at 70%. It is very natural to perceive a trend and to presume that the probability is more likely to next increase to 80% rather than decrease to 60%. For many types of data — economic or social — such trends really do happen often. But probabilities don’t work that way!

The three figures below indicate possibilities and impossibilities. Each figure shows 6 typical “realizations”, that is ways in which probabilities of a given event might change over time. We take the initial probability as 50% and make 3 of the realizations end at 1 (the event occurred) and the other 3 ends at 0 (the event did not occur).

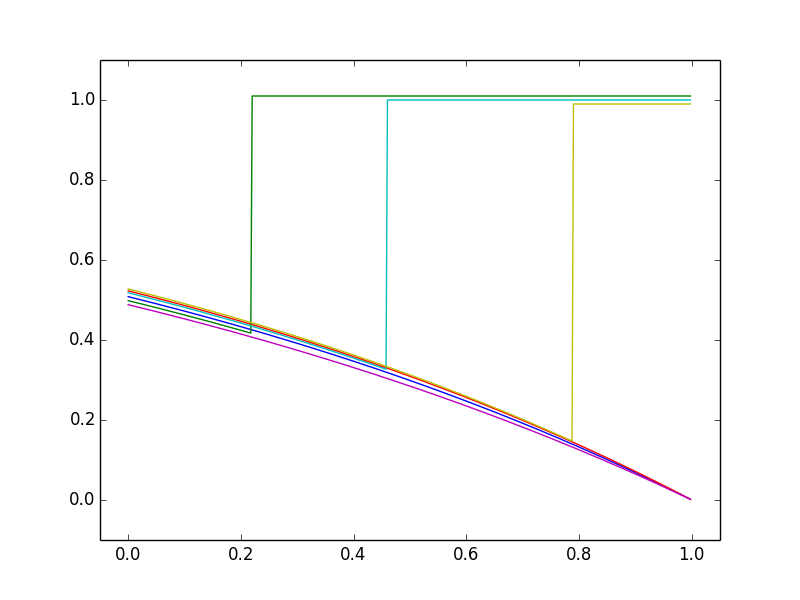
This first figure illustrates the context of whether a major earthquake will occur in a given place before a given deadline (taken far ahead, so the current probability is 0.5). Assuming earthquakes remain unpredictable, the figure shows possible graphs of how the probability changes with time up to the deadline. Here one’s intuition is correct: probabilities decrease as long as the earthquake hasn’t happened but jump to 1 if it does happen.

This second figure illustrates a context in which new information only makes small changes to one’s assessed probabilities. In this case, the changes must vary in direction (up and down) which leads to the “jagged” curves in this second figure. This is reminiscent of stock market prices, which is no coincidence. Under the classical “rational” theory, stock prices reflect ongoing estimates of discounted future profits, which mathematically fit this context, at least in a short term.

The latter is itself a notable insight from mathematical probability. The characteristic jagged shape of stock prices is not specific to the context of stocks or finance but is a general feature of slowly varying assessments of likelihoods of future events.

The first two figures show what can happen — they are extreme cases, and other cases may incorporate both small continuous changes and big jumps. The third figure below indicates what “the picture becomes clearer” analogy would suggest — that probabilities should change only by moving closer to the ultimate outcome. This cannot happen regularly (note it happens for some realizations in the first figure).

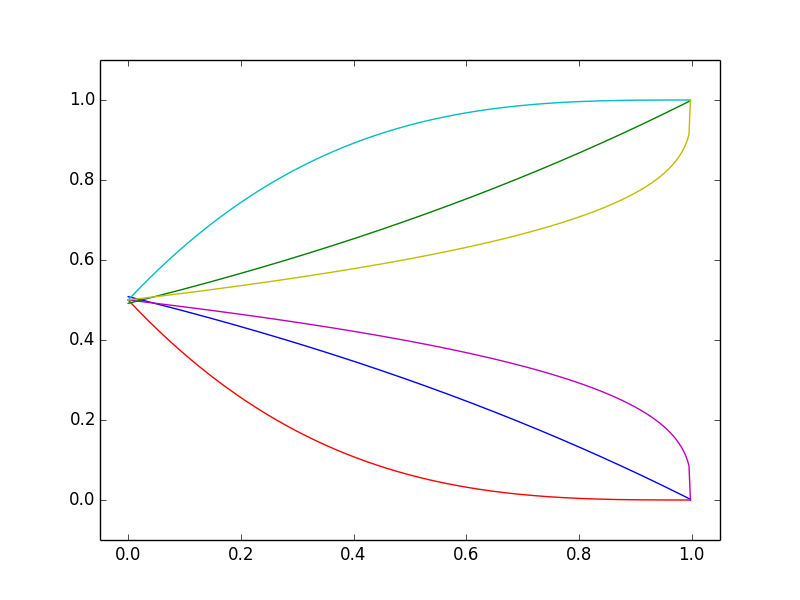
Why not? Basically, because the assertions

(a) the probability now is 60%

(b) the probability will increase to 70%

are contradictory; (b) would imply the probability is already 70%.

Notes

Mathematically this is part of martingale theory. Here is a technical paper on the psychology of the erroneous trend effect belief.

Bio: David Aldous is Professor in the Statistics Dept at U.C. Berkeley, since 1979. He received his Ph.D. from Cambridge University in 1977. He is the author of “Probability Approximations via the Poisson Clumping Heuristic” and (with Jim Fill) of a notorious unfinished online work “Reversible Markov Chains and Random Walks on Graphs”. His research in mathematical probability has covered weak convergence, exchangeability, Markov chain mixing times, continuum random trees, stochastic coalescence, and spatial random networks. A central theme has been the study of large finite random structures, obtaining asymptotic behavior as the size tends to infinity via consideration of some suitable infinite random structure. He has recently become interested in articulating critically what mathematical probability says about the real world.

He is a Fellow of the Royal Society and a foreign associate of the National Academy of Sciences.

“Bayesian Updating and the “Picture Becomes Clearer” Analogy was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI