
Differentiability of a Function Given its Graph
Last Updated on August 7, 2023 by Editorial Team
Author(s): Sujeeth Kumaravel
Originally published on Towards AI.

Consider the function:
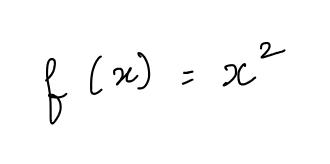
Its graph is:

The derivative of a function at a point is the slope of the tangent to the function at that point. For this function, the derivative exists at all points x in its domain. But, this is not the case for all functions. There are functions for which derivatives don’t exist at all points in their domains. In this article, we will see three types of points at which a function will not have a derivative; that is, it is not differentiable.
A function is formally defined as differentiable if its derivative exists at all points x in its domain. That is, if you can compute a unique value at each point in its domain, it is called differentiable.
A function is considered continuous if you can draw its graph without lifting your pencil up from the paper.
Let us consider the function f(x) = U+007CxU+007C. It is defined as :

Its graph is drawn as:

This is a continuous function. Let us draw a tangent at x=0. It can be drawn as (the red line is the tangent):

But, another tangent can be drawn at x=0 as:

This line also touches the function at only one point i.e. x=0. So, it is indeed a tangent. In fact, for this function, there are multiple such tangent lines possible at x=0:
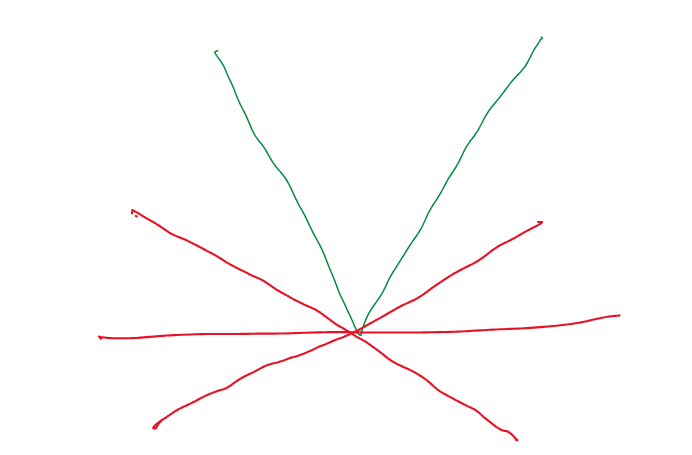
This means there is no unique value for the slope of the tangent at x=0.
Let’s look at the limit calculations as well.
The derivative of f(x) is defined as the value of the following limit:

Let’s compute the one-sided limits:
Left limit:

Right limit:

Left limit = -1 and right limit = 1. They disagree. So, there is no unique value for the limit and so it doesn’t exist. So, f(x) = U+007CxU+007C is not differentiable at x=0. This kind of function is said to be having a corner (also called a cusp or a sharp turn). Such functions are non-smooth. An example graph of such a function is:

This function has a corner at x=a.
A discontinuous function such as the one shown below is also non-differentiable at the point of discontinuity because the left and right limits will disagree:

Note:
- The point at which a function takes a value of infinity is also called a discontinuity.
- When the function’s value is a single point value, that is also a discontinuity, as shown below. This function has a single point value of 2 at x=a:

A function is non-differentiable at the point where the tangent line is vertical because, at that point, the tangent has a slope that is undefined (infinity). An example of such a function is shown below (the red line is the tangent at x=a):

Hence there are three types of points at which a function is not differentiable:
- corner (or cusp or sharp turn)
- discontinuity (jump, infinity, point)
- vertical tangent (slope is undefined)
What are the points at which the following function is not differentiable?

The points are:
- corners -> -3
- discontinuity -> -10, 1, 4
- vertical tangent -> -8
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI














