Beyond Labels: The Magic of Autoencoders in Unsupervised Learning
Last Updated on November 3, 2024 by Editorial Team
Author(s): Shivam Dattatray Shinde
Originally published on Towards AI.
In a world where labeled data is often scarce, autoencoders provide a powerful solution for extracting insights from unstructured data without the need for manual supervision.
Agenda
- Unlabeled Data
- Auto-Encoders: Loss Function, Bottleneck, Denoising Auto-Encoder
- Unsupervised Pre-training Using Auto-Encoders
- Code Demonstration
Unlabeled Data
In many applications, such as object recognition and detection, collecting labeled data is challenging, while unlabelled data is relatively easy to gather. We can leverage this abundant unlabelled data to enhance the performance of our models.
A useful approach is to use the unlabeled data to learn meaningful representations of the input features. In image-related tasks, for example, the early layers of a neural network typically learn basic abstract features of an image, such as edges and other basic shapes. By using a large amount of unlabeled data, we can train the network to extract these foundational features. Once these abstract representations are learned, we can then train the new neural network, with the abstract features serving as inputs. This approach generally leads to improved model performance.
A type of neural network called ‘Autoencoder’ is used to calculate this representation.
Auto-Encoders

Here,
Let X1, X2, …, Xm represent the inputs to the auto-encoder neural network, h1, h2, …, hk represent the condensed or essential features of the input, and the reconstructed outputs are denoted by X1′,X2′,…,Xm.
In this network, we feed image pixels as input. The middle hidden layer captures the condensed essence or representation of the input features. The goal is to then reconstruct the original input from this condensed representation.
The first part of the network, where the input is transformed into its essential features, is known as the encoder. The second part, where the essence is used to reconstruct the original input, is called the decoder.
For auto-encoder neural networks, the number of neurons in hidden layers first decrease during the encoder part and then increases during the decoder part of the network.
Note that I have shown only one hidden layer in the figure. However, we can have multiple hidden layers in the encoder and decoder part of the network. Also, we can have different numbers of hidden layers in the encoder and decoder part of the neural network.
Auto-encoder training loss function
With an auto-encoder, our main goal is to create the values of outputs (reconstructed inputs) that are as close as possible to the inputs. We can use Mean Squared Error as a performance measure.
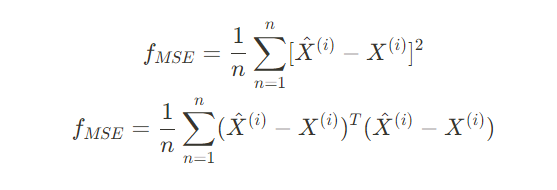
This loss is called reconstruction loss. So, in short, our goal is to minimize this reconstruction loss.
Note that reconstruction loss function does not require any training labels.
Bottleneck
If number of neurons in input (m) is equal to a number of neurons in hidden layer (k), then consider the case where the activation function is linear, W1 = W2 = I (identity matrix), and b1 = b2 = 0.
In this case, input and reconstructed values will be equal but the model won’t learn proper essence of input in the hidden layer.
For this reason, we generally set k < m. Therefore, hidden layer is called a bottleneck.
Denoising AutoEncoder

However, there is a way we can use k ≥ m.
If we first add some noise to the inputs and then use the auto-encoder to reconstruct the original inputs without noise, then we can use k ≥ m. Even if the activation is linear and W1 = W2 = I (identity matrix), b1 = b2 = 0, then also we won’t get zero reconstruction error.

We are adding the noise N(0, I) to the input and we will try to reconstruct the input X using the autoencoder.
Unsupervised Pre-training using Auto-Encoder

After training the autoencoder, W1, and b1 learn to extract the useful features from the input. Now we can use these extracted features for different tasks, such as image classification.
Usually, extracted feature from the hidden layer is of smaller dimension than the input. So, this works kind of like dimensionality reduction.
Also, if we used the extracted features for classification, then we might get a better performance than normal classification in most cases. This is because the encoder is trained on much larger unlabelled dataset. So, it learns the abstract features of the image better than when we use the smaller dataset for the classification task.
We ‘chop-off’ the decoder part of auto-encoder and then add new layers after the encoder part to create a new neural network for the classification.
During the training of classification model, we only train the neurons in the secondary network. But we can fine-tune the trained auto-encoder with a small learning rate or we can even make the encoder layers untrainable.
Now, let’s see how to use auto-encoders for unsupervised pretraining using the code.
Code Demonstration
We will be using MNIST Fashion dataset for out task.
Importing required libraries and preprocessing the data
# Importing required libraries
import warnings
warnings.filterwarnings('ignore') # Suppress any warnings during execution
import numpy as np
import tensorflow as tf
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras.callbacks import EarlyStopping
from sklearn.metrics import accuracy_score
# Loading the MNIST dataset
# - mnist.load_data() returns two tuples: (training data, training labels) and (test data, test labels)
mnist = tf.keras.datasets.mnist
(x_train, y_train), (x_test, y_test) = mnist.load_data()
# Normalizing the data by scaling pixel values from [0, 255] to [0, 1]
x_train, x_test = x_train / 255.0, x_test / 255.0
# Reshaping the data:
# - Each image is originally 28x28 pixels, but the input to the autoencoder is a flattened vector of length 784
x_train = x_train.reshape(-1, 784)
x_test = x_test.reshape(-1, 784)
Training the encoder network
# Creating an autoencoder model
# Input layer: expects a 784-dimensional vector (flattened image)
ip = tf.keras.layers.Input(shape=(784,), name='input')
# Encoder layers: gradually compress the input down to a lower-dimensional representation
x = tf.keras.layers.Dense(512, activation='relu', name='encoder1')(ip) # First hidden layer with 512 units
x = tf.keras.layers.Dense(256, activation='relu', name='encoder2')(x) # Second hidden layer with 256 units
x = tf.keras.layers.Dense(128, activation='relu', name='encoder3')(x) # Third hidden layer with 128 units
# Essence layer: final compressed representation of the input (latent space) with 64 units
essence = tf.keras.layers.Dense(64, activation='relu', name='essence')(x)
# Decoder layers: reconstruct the compressed input back to the original dimensionality
x = tf.keras.layers.Dense(128, activation='relu', name='decoder1')(x) # First decoding layer with 128 units
x = tf.keras.layers.Dense(256, activation='relu', name='decoder2')(x) # Second decoding layer with 256 units
x = tf.keras.layers.Dense(512, activation='relu', name='decoder3')(x) # Third decoding layer with 512 units
# Output layer: reconstruct the 784-dimensional input using the same shape as the original data
op = tf.keras.layers.Dense(784, activation='relu', name='reconstructed_input')(x)
# Define the autoencoder model
# - inputs=ip: input layer
# - outputs=op: output layer (reconstructed input)
model = Model(inputs=ip, outputs=op)
# Compile the model
# - optimizer: Adam (adaptive optimizer)
# - loss: MSE (mean squared error, suitable for reconstruction tasks)
# - metrics: accuracy (monitors the training process)
model.compile(optimizer='adam', loss='mse', metrics=['accuracy'])
# Display the summary of the model architecture
model.summary()
# Define early stopping to prevent overfitting
# - monitor='val_loss': stops training when the validation loss stops improving
# - min_delta=0: minimum change in monitored quantity to qualify as an improvement
# - patience=10: the number of epochs to wait for improvement before stopping
# - verbose=1: displays messages when training is stopped early
# - mode='auto': automatically infers the direction (minimize loss or maximize metric)
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0, patience=10, verbose=1, mode='auto')
# Train the model using the autoencoder framework
# - x_train as both input and output (autoencoders reconstruct the input, so the target is the same)
# - epochs=20: train for a maximum of 20 epochs
# - batch_size=2048: large batch size to process more samples at once (helps with memory efficiency)
# - validation_data: (x_test, x_test) since we're also validating the model's ability to reconstruct test data
# - callbacks: include early stopping to halt training if no progress is made
history = model.fit(x_train, x_train, # input and output should both be the training data for autoencoders
epochs=20,
batch_size=2048,
validation_data=(x_test, x_test), # likewise for validation data
callbacks=[early_stopping])


Getting the essence layer of the encoder for later classification tasks
# Define the encoder model
# - inputs=ip: the input layer of the original autoencoder (784-dimensional input)
# - outputs=essence: the output from the 'essence' layer (64-dimensional latent representation)
# This model will act as the encoder, taking the original input and producing the compressed representation (latent space)
encoder = Model(inputs=ip, outputs=essence)
Training the classfication model without using auto-encoder’s extracted features
import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Model
from tensorflow.keras.callbacks import EarlyStopping
from sklearn.metrics import accuracy_score
# Define the neural network model
ip = tf.keras.layers.Input(shape=(784,), name='input') # Input layer with 784 features (for flattened 28x28 images)
x = tf.keras.layers.Dense(128, activation='relu')(ip) # Dense layer with 128 units and ReLU activation
x = tf.keras.layers.Dense(64, activation='relu')(x) # Dense layer with 64 units and ReLU activation
output = tf.keras.layers.Dense(10, activation='softmax')(x) # Output layer with 10 units (for 10 classes) and softmax activation
# Create the model that connects the input layer to the output layer
normal_model = Model(inputs=ip, outputs=output)
print("Normal Model Summary:\n")
print(normal_model.summary())
# Compile the model
# - Optimizer: Adam (adaptive learning rate optimization)
# - Loss: sparse_categorical_crossentropy (suitable for integer labels, which are not one-hot encoded)
# - Metrics: accuracy (to monitor model performance during training)
normal_model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# Early stopping to prevent overfitting:
# - monitor: validation loss
# - patience: wait for 10 epochs with no improvement before stopping
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0, patience=10, verbose=1, mode='auto')
# Train the model:
# - x_train: training data (input)
# - y_train: training labels (target)
# - epochs: 20 (how many times the model will iterate over the training data)
# - batch_size: 2048 (number of samples per batch)
# - validation_data: (x_test, y_test) (validation data to monitor performance on unseen data)
# - callbacks: use early stopping to prevent overfitting if validation loss doesn't improve
normal_model.fit(x_train, y_train,
epochs=20,
batch_size=2048,
validation_data=(x_test, y_test),
callbacks=[early_stopping])
# Make predictions on the test data:
# - y_hat_prob: the model returns the predicted probabilities for each class (shape: [num_samples, 10])
y_hat_prob = normal_model.predict(x_test)
# Convert the predicted probabilities to class predictions:
# - np.argmax: selects the index of the highest probability (i.e., the predicted class)
y_hat = np.argmax(y_hat_prob, axis=1)
# Calculate accuracy:
# - Compare the predicted labels (y_hat) with the true labels (y_test) using accuracy_score
acc = accuracy_score(y_test, y_hat)
# Print the accuracy of the model on the test set
print(f'Accuracy: {acc}')


Note that we are getting approximately 97.38% accuracy over the testing data when we don’t use the auto-encoder’s extracted features.
Training the classfication model using auto-encoder’s extracted features (Unsupervised Pretraining)
# Freeze the encoder layers to prevent them from being updated during training (Optional)
for layer in encoder.layers:
layer.trainable = True # Not freezing layers
# Define the model that will be trained on the encoded data
ip = tf.keras.layers.Input(shape=(784,), name='input') # Input layer expecting 784 features (encoded input)
x = encoder(ip) # Use the pre-trained encoder to process the input
x = tf.keras.layers.Dense(128, activation='relu')(x) # First dense layer with 128 units and ReLU activation
x = tf.keras.layers.Dense(64, activation='relu')(x) # Second dense layer with 64 units and ReLU activation
output = tf.keras.layers.Dense(10, activation='softmax')(x) # Output layer with softmax for 10 classes
# Create the model that includes the frozen encoder and new classification layers
pretrained_model = Model(inputs=ip, outputs=output)
print("Normal Model Summary:\n")
print(pretrained_model.summary())
# Compile the model using Adam optimizer and sparse categorical crossentropy loss (for integer labels)
pretrained_model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
# Early stopping to prevent overfitting; stops if validation loss doesn't improve for 10 epochs
early_stopping = EarlyStopping(monitor='val_loss', min_delta=0, patience=10, verbose=1, mode='auto')
# Fit the model on training data (x_train) with validation on x_test
pretrained_model.fit(x_train, y_train, # Train with original input data and integer labels
epochs=20,
batch_size=2048,
validation_data=(x_test, y_test), # Validate on test data and labels
callbacks=[early_stopping])
# Predict the class probabilities on the test set
probs = pretrained_model.predict(x_test)
# Convert probabilities to class predictions using argmax (highest probability wins)
y_hat = np.argmax(probs, axis=1)
# Calculate accuracy by comparing predictions (y_hat) to actual labels (y_test)
acc = accuracy_score(y_test, y_hat)
print(f'Accuracy: {acc}')


Note that we are getting approximately 97.84% accuracy over the testing data when we use the auto-encoder’s extracted features. This is better accuracy as compared to when we don’t use auto-encoder’s extracted features.
Also, note that I have made the encoder’s layers trainable in this case. But we can also freeze encoder’s layers and only train the secondary network. Optionally, we can also train the encoder using very learning rate.
Outro
Thank you so much for reading. If you liked this article, don’t forget to press that clap icon. Follow me on Medium and LinkedIn for more such articles.
Are you struggling to choose what to read next? Don’t worry, I have got you covered.
The Tug of War: Accuracy and Interpretability in Machine Learning Models
Agenda:
ai.plainenglish.io
and one more…
Efficient Backpropagation: Exploring the Role of Jacobian Matrices and the Chain Rule
In this article, I will tough upon the topic of Jacobian matrix and how it is used in the back-propagation operation of…
ai.plainenglish.io
Have a great day!
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














