Understand AI Interpretability & Explainability

Author(s): Stavros Theocharis

Originally published on Towards AI.

Future trust depends on precise definitions

Introduction

It has become an urgent expectation to interpret and demystify black-box algorithms to increase their adoption. A growing number of organizations have begun to adopt Artificial Intelligence (AI) and Machine Learning (ML) for their crucial business decision-making procedures. This is in an effort to increase the adoption of these technologies. AI and ML are progressively being employed for the purpose of defining our day-to-day activities in a variety of domains, including finance, healthcare, education, recruiting, transportation, and supply chain, to name a few. But because AI and ML models play quite an important role, business stakeholders and consumers are becoming increasingly concerned about the models’ inability to be transparent and interpretable. This is because black-box algorithms are highly susceptible to human bias. Model explainability is essential for high-stakes domains such as healthcare, finance, the legal system, and other critical industrial operations.

In modern healthcare facilities, for example, data analysis on patient health is performed with the use of models that take into account a diverse range of factors. These algorithms are able to provide very precise predictions about the chance that a patient will suffer from a certain health condition. It is no longer just a suggestion but rather a choice that is guided by evidence, despite the fact that a doctor may or may not ultimately make the diagnosis.

What could possibly be wrong with that?

What are the odds that this is indeed the case?

To interpret a machine learning model’s decisions, one needs to find meaning in the model’s output. You can also trace the output back to its original source and the transformation that created it.

Machine learning interpretation

I’ll give you a simple example to help you understand the concept of interpretation. So, simple linear regression is considered one of the basic models:

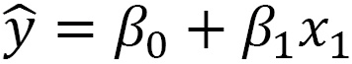
• yhat is the dependent variable
• β0 and β1 are considered the constant, and the coefficient accordingly
• x1 is the independent variable

Let’s introduce 2 new variables in the positions of yhat and x1. These are the income and education:

income = b0 + b1 education

Let’s also suppose a simple example that education is measured in years and income in $.

So, supposing a new regression model with bo=500 and b1=100:

income_i = b0 + b1 education_i + ε_i

This means that for each additional year of education, the person gets $100 more on average. So, for example, someone who has been in school for six years will earn $1100 (as a prediction of the above model).

One of the many ways that this model of linear regression may be described is by describing how the model itself operates, which is also one of the possible explanations. Having said that, this is just one perspective on the situation. Due to the fact that the actual results and the projected outcomes for the training set do not correspond with one another, the model is not infallible. The disparity (ε_i) between the two is referred to as the error, although it is also sometimes called the residuals.

When assessing an error in a model, there are several different angles from which one might approach the problem. You may make use of an error function such as “mean absolute error” in order to quantify the degree to which the values that were actually obtained deviate from those that were predicted.

When performing linear regression, the assumptions that someone has to test are homoscedasticity, linearity, normalcy, independence, and a lack of multicollinearity (if there is more than one feature). These assumptions make sure that the best model is being used for the problem at hand. When we have a better understanding of how a model operates and under what conditions it does so, we are better able to explain why it might generate particular predictions and when it doesn’t.

In the preceding example, what would happen if we wanted to explain why an individual with 6 years of education is anticipated to make $1100 but, in fact, earns only $800? This is an issue that often occurs. This is why we use the phrase “on average”. Therefore, it should be anticipated that there will be circumstances in which the model will not be as reliable.

What else would happen if we utilized this model to forecast values that have not yet been seen? For illustration’s sake, let’s pretend that it was trained on data ranging from 0 to 10 years of education and that we now have a case with 12 years of education.

The earlier model takes on a straightforward form. In order to achieve a higher level of accuracy, we will need to include a greater number of variables.

Let’s include them…..

But wait a minute! What variables?

Some of them are mentioned in the bibliography for such problems, such as job experience, age, industry, etc. Would it be reasonable to add others? Perhaps the individual’s gender or location?

If the data that we obtained was solely based on males, then we do not know how accurate the results are for females (this is an example of selection bias), and what if the income had more to do with social standards and characteristics that are not included as variables (this is an example of omitted variable bias)?

Many questions that need to be answered…..

Another thing that needs to be done thereafter is to explain whatever features of the model (or variables) have an effect on the performance of the model (feature importance). We must be careful not to make things worse. Why?

Increasing the number of features leads to an increase in complexity.

This results in additional challenges when attempting to interpret the model. Interpretable ML is fully connected with the “FAT”. “FAT” comes from the words “fairness”, “accountability” and “transparency”.

How can all of this make any kind of sense?

• Can you explain your predictions without discernible bias? -> fairness
• Can you explain why we have specific predictions? -> accountability
• Can you explain how predictions are being generated and, in general, the model functionality?-> transparency

FAT has been transformed into FATE as a result of efforts made by several academics and businesses to place it under the broader umbrella of ethical artificial intelligence (AI). The regulation of algorithmic and data systems is even more of a broad topic than the ethical use of AI. Nevertheless, there is a substantial amount of overlap between the two notions due to the fact that interpretable machine learning is the means through which FAT principles and ethical concerns are applied in machine learning.

Interpretability

In most cases, researchers would use the words interpretability and explainability interchangeably. Despite the fact that these terms are quite closely linked to one another, there are certain studies that pinpoint their distinctions and separate these two ideas. Nevertheless, a number of efforts have been made [2] in order to define not only these terms but also relevant topics such as comprehensibility.

There is currently no tangible mathematical concept for interpretability or explainability, nor have they been analyzed by some metric. None of these definitions make use of mathematical formality or rigor [3]. Doshi-Velez and Kim, in their work [4], describe interpretability as “the ability to explain or to convey in intelligible words to a human”, which is one of the definitions of interpretability that is considered to be among the most widely accepted ones.

Another prominent definition of interpretability was provided by Miller T. (2019), where he specifies it as “the extent to which a human is able to grasp the reason for a choice” [5]. Even if they make sense intuitively, these definitions are neither mathematically rigorous nor formal. Based on Masis S. (2021), I will try to keep up with a specific differentiation between them [6].

The term “interpretability” refers to the degree to which human beings are able to comprehend the inputs and outputs, as well as the causes and effects, of a machine learning model. If you are able to describe the conclusion that a model generates in a way that can be understood by humans, then you will be able to say that the model has a high degree of interpretability. To phrase it another way, the question is: why does a particular input into a model result in a specific output? When it comes to the data that is being input, what are the requirements and constraints? Where do we stand currently in terms of the confidence levels of the predictions? Or, why does one character have a significantly greater influence than the others? In the context of interpretability, the particulars of a model’s operation are only relevant if the model can demonstrate both that it is the proper model for the use case and that it can explain how its predictions were arrived at.

In the first example, we may claim that there is a linear link between income and education; hence, it makes more sense to use linear regression rather than a non-linear approach. Statistical analysis will allow you to demonstrate this, provided that the variables in question do not contradict the presumptions of linear regression. Even though the data is on our side, you should still consult with the domain expertise are involved in the use case.

From dataset selection through feature selection and engineering, as well as choices regarding model training and tuning, many decisions are taken, each of which has the potential to enhance model complexity and decrease its interpretability. Because of its intricacy, describing how it operates is a difficult task.

The interpretability of machine learning is a highly active field of study, and as a result, there is still a great deal of controversy about its exact definition. The question of whether or not complete transparency is required for a machine learning model to be considered adequately interpretable has been brought up in the discussion. It is not necessary for the concept of interpretability to exclude opaque models, which are often complicated, as long as the choices taken do not impair the trustworthiness of the model. This kind of concession is what many in the industry term “post-hoc interpretability.” In post-hoc machine learning interpretation, a person explains the model’s logic on behalf of the machine learning model.

Do we need interpretability?

The capacity to understand decisions is not always necessary for decision-making systems. There could be a few exceptions: when incorrect results have no significant consequences. For example, suppose we have a use case where we want to use a computer vision application to count the number of cars in a specific area. If the model sometimes underestimates the total number of cars, there is probably no discriminatory bias and the cost will be relatively low (this means that the possible loss of the prediction does not cost too much).

Interpretability is crucial, for example, in self-driving cars, where it is needed to understand possible points of failure. In addition, it is important in cases like LLMs that may produce unethical results based on gender or race.

It is possible for us to fill in the blanks in our knowledge of the issue if we explain the choices that a model makes. Given the excellent accuracy of our machine learning algorithms, we have a tendency to enhance our level of confidence to the extent that we believe we completely comprehend the problem. This is among the most critical challenges, and it contributes to one of the most serious problems.

Before continuing with explainability, let’s see what the black box and white box models are….

Black box and White box models

Simply put, “black box” is another name for models that are opaque. A system is said to have the characteristics of a “black box” if it can only be seen from the outside in terms of its inputs and outputs, while the internal workings of the system remain hidden from view. A black-box model may be opened up in the context of machine learning; nevertheless, the workings of the model are not straightforward to comprehend.

White box models are the reverse of the black box approach. They attain complete or very close to complete interpretive transparency, which is why they are often known as transparent. In reality, they are straightforward models such as linear regression.

Explainability

Everything that interpretability entails is included in explainability as well. The distinction is that it extends farther on the criteria of interpretability than it does on the need for transparency. This is because it requires human-friendly explanations for the “insides” of a model as well as the process of training a model, in addition to merely model inference. This criterion could include varying degrees of the model, design, and algorithmic transparency, depending on the application that’s being used.

There are several parts of transparency:

Model transparency: The ability to describe how a model is trained on a step-by-step basis.

Design transparency: Having the ability to provide an explanation for decisions such as the model architecture and hyperparameters used. For instance, we may defend these decisions by referring to the scale of the training data or the kind of information it contains.

Algorithmic transparency: The capability of explaining how automated optimizations work. Random searches like random hyperparameter optimization or stochastic gradient descent make the total pipeline non-transparent.

Other concepts that can affect the trust in models and also their explainability are “statistical-grounded”, “non-reproducibility,” “overfitting,” “the curse of dimensionality,” “human cognition,” and “Occam’s razor”.

Do we need explainability?

The capacity to make decisions that are both trustworthy and ethical is the primary driver behind explainability. There are a number of other factors that contribute to explainability, including causality, transferability, and informativeness. As a result, there are a lot of different use cases in which complete or almost complete transparency is prized, and this is quite appropriate.

In the end, everything leads to trust…..

So, the next time you have a new model ready, ask yourself: Can I explain my model?

This will automatically answer the question: Do I trust this model?

References

[1] Abraham C., Sims R., Daultrey S., Buff A., Fealey A. (2019). How Digital Trust Drives Culture Change. MITSloan Management Review

[2] Lipton Z.C. (2018). The mythos of model interpretability. Queue, 16, 31–57

[3] Adadi A., Berrada M. (2018). Peeking inside the black-box: A survey on Explainable Artificial Intelligence (XAI). IEEE Access, 6, 52138–52160

[4] Doshi-Velez F., Kim B. (2017). Towards a rigorous science of interpretable machine learning. arXiv

[5] Miller T. (2019). Explanation in artificial intelligence: Insights from the social sciences. Artif. Intell., 267, 1–38

[6] Masis S. (2021). Interpretable Machine Learning with Python. Packt Publishing. Birmingham, UK

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI