Review: IDECNN-Improved Differential Evolution of Convolutional Neural Network (Image Classification)

Author(s): Arjun Ghosh

Originally published on Towards AI.

Review: IDECNN-Improved Differential Evolution of Convolutional Neural Network (Image Classification)

In this story, our research paper, titled: “Designing optimal convolutional neural network architecture using differential evolution algorithm” [1], is reviewed. The article highlights the use of Differential Evolution (DE) as a search strategy to address the Neural Architecture Search (NAS) approach. The research employed eight well-known imaging datasets and concluded that IDECNN (proposed method) had the ability to design a more appropriate architecture in contrast to 20 already existing CNN models. This research is published in Patterns, Elsevier in 2022.

Outline

1. Introduction
2. Overall Framework
3. Brief Discussion
4. Results and Conclusion
5. Introduction

The article discusses the challenges of manually designing Convolutional Neural Networks (CNNs) for various tasks, specifically image classification. To address this issue, the article recommends the Neural Architecture Search (NAS) approach, which automates the design of CNN architectures. The article emphasizes that meta-heuristic approaches, such as Differential Evolution (DE), have become a popular and effective search strategy for NAS. The proposed approach in the article is an improved DE-based method that automates the design of layer-based CNN architecture for image classification tasks.

2. Overall Framework

The framework of the proposed work is in [1].

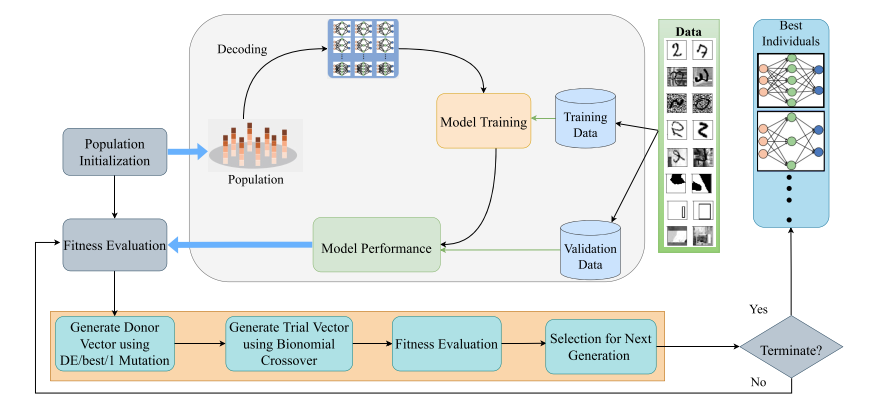
The paragraph outlines an algorithm proposed for creating an ideal architecture for a CNN model to be used for image classification. Initially, a group of CNN architectures is randomly initialized and trained on a section of the training data, after which they are rated based on their validation dataset fitness function. The fitness function is based on classification errors. Individuals undergo mutation and crossovers during the DE process to produce updated architectures that are assessed for fitness. The fittest individuals in each generation are selected based on their fitness function, and this process is continued until a stopping condition is met. The optimal CNN architecture is chosen based on the lowest fitness score of the best-selected individuals and is tested on the test dataset to determine its final performance.

3. Brief Discussion

The paragraph discusses the initialization process of the population in the Neural Architecture Search (NAS) algorithm proposed in the paper. A population is a group of N individuals that are randomly located within the search space. Each individual is made up of Convolution, Pooling, and Fully-Connected (FC) layers with randomly chosen hyper-parameters. Each individual has a limited length and must have a Convolution layer as the first component and an FC layer as the last component. The hyper-parameters of each layer are selected from predetermined ranges, while other parameters are based on previous studies.

The passage discusses the utilization of mutation within the framework of evolutionary computing, specifically in optimizing Convolutional Neural Networks (CNNs) through the Differential Evolution (DE) algorithm. In this approach, the DE/best/1 mutation scheme is employed to create a donor vector vi for each target vector xi in the current generation. The proposed method, IDECNN, calculates the difference between two individuals (xr1, xr2) in the population (P) that are distinct from the target vector, considering their component layer types. If the jth dimension of the randomly selected individuals has the same layer type, their associated hyperparameters values are subtracted. If the values of the jth dimension in xr1 and xr2 are different in terms of layer type, the algorithm will copy the jth layer from xr1, including its corresponding hyper-parameters, to represent the difference between the two. The best individual from the population is chosen after boundary checking, and a scaling factor F and a random number r are used to select a layer from xbest or (xr1-xr2) to compute the donor vector vi. Equation (3) in reference [1] outlines the proposed mutation operation, which is as follows:

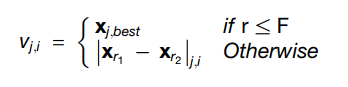
The proposed algorithm employed a crossover operation to enhance variation in the population. The mutation generated a donor vector, which was then used to produce a trial vector by crossing it with the target vector. The paper used binomial crossover, which was based on a crossover rate and a random number. The length of the donor vector was established, and a random value was selected within its range. For each dimension of the trial vector, a random number was generated. If the random number was less than the crossover rate or was the same as the chosen value, the corresponding value was taken from the donor vector. If not, it was taken from the target vector. An instance of this process is presented in Figure 6 of the reference [1].

During the selection stage, the fitness of each individual in the population is assessed by calculating the classification loss error based on a fitness function. The fitness of the trial vector ui obtained through crossover and mutation is also determined. The target vector xi and trial vector ui are compared based on their minimum loss error values, and the superior individual is selected for the next generation. This selection process maintains a constant population size and increases the chances of selecting individuals with superior fitness values for the next generation. Equation (4) in reference [1] provides the proposed selection operation, which is as follows:

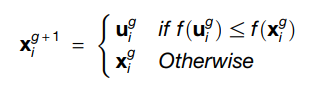
4. Results and Conclusion

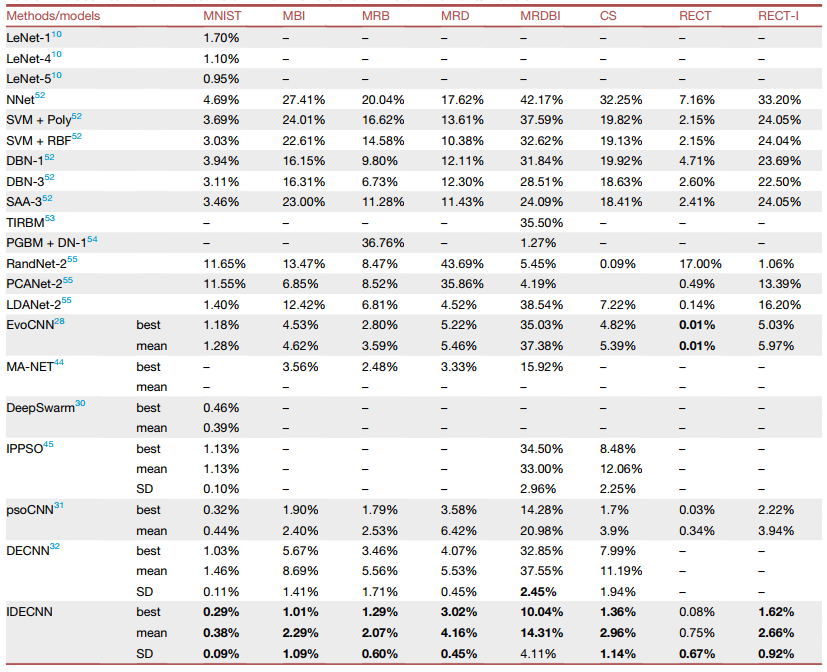Classification error results of IDECNN and state-of-the-art methods/models. The table is taken from [1].

To summarize, the IDECNN method was tested on eight commonly used image datasets, and the findings demonstrated that it outperformed other state-of-the-art methods on six of the eight datasets based on the best mean, and SD of classification error rate. Notably, IDECNN achieved the best performance on the MNIST dataset, with the best error rate of 0.29%, a mean error rate of 0.38%, and an SD error rate of 0.09%. Additionally, it demonstrated superior performance on the MBI, MRB, MRD, CS, and RECT-I datasets. These results indicated that the proposed IDECNN approach is effective in generating CNN architectures that can achieve high accuracy in image classification tasks. Further, the generated CNN architectures are applied in the image classification of real-world applications involving X-ray biomedical images of pneumonia and coronavirus disease 2019 (COVID-19). The outcomes indicate the effectiveness of the proposed approach in generating an appropriate CNN model.

Reference:

[Patterns, Elsevier] [2022]

1. Designing optimal convolutional neural network architecture using differential evolution algorithm

---

Review: IDECNN-Improved Differential Evolution of Convolutional Neural Network (Image… was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI