Baby Steps to TensorFlow

Author(s): Lawrence Alaso Krukrubo

Originally published on Towards AI.

Tutorial on Creating a Simple TensorFlow Model U+007C Towards AI

Training your first Tensorflow based Neural Network model for Celsius to Fahrenheit conversion

TensorFlow is an open-source machine learning library for research and production. It offers APIs for beginners and experts to develop for desktop, mobile, web, and cloud. See link.

A software library is a set of functions and modules that you can call, through your codes to perform certain tasks.

Before proceeding, I would assume you’re comfortable coding in python and have some basic knowledge about Machine Learning.

TensorFlow is arguably the most popular Machine Learning library on GitHub. It is based on the concept of a computational graph.

In a computational graph, nodes represent either persistent data or a Math operation, and edges represent the flow of data between nodes. The data that flows through these edges is a multi-dimensional array known as a tensor, hence the library’s name, “TensorFlow”.

We’ll try to keep things simple here, and only introduce basic concepts.

The problem we would solve is to convert values from Celsius to Fahrenheit using a simple TensorFlow model, where the approximate formula is:

Fahrenheit = Celsius * 1.8 + 32

This means to manually convert 30-degree Celsius to Fahrenheit, all we need do is multiply 30 by 1.8, then add 32 to the result and that gives 86. see link

Of course, it would be simple enough to create a conventional Python function that directly performs this conversion, but that would not be machine learning.

Instead, we’ll give TensorFlow some sample Celsius values and their corresponding Fahrenheit values. Then, we’ll train a model that figures out the above formula through the training process. And we’d use the model to convert arbitrary values from Celsius to Fahrenheit and finally evaluate the model.

Primer:

Neural Networks:

A Neural Network is basically a set of functions which can learn patterns.

In traditional programming, we pass in the rules to a program and the data set for that program and the computer returns the answers.
In Machine Learning, we basically pass the answers and as much data as we can about examples (pairs of features and labels) to the computer and the computer figures out the rules to accurately predict or determine the answers to future unseen data.

Import dependencies

First, import TensorFlow as tf for ease of use. We’d also tell it to only display error logs if any.

import tensorflow as tf
tf.logging.set_verbosity(tf.logging.ERROR)import numpy as np
import matplotlib.pyplot as plt

Setting up the training data:

Since the task is to create a model that can predict the Fahrenheit values when given Celcius degrees, we shall create two lists for training the model. One for Celsius degrees and the other for corresponding Fahrenheit values.

# Let's create two lists for celsius and fahrenheit using numpycelsius_q = np.array([-40, -10, 0, 8, 15, 22, 38], dtype=float)fahrenheit_a = np.array([-40, 14, 32, 46, 59, 72, 100], dtype=float)# Let's iterate through the list and print out the corresponding #valuesfor i,c in enumerate(celsius_q):
 print("{} degrees Celsius = {} degrees Fahrenhet".format(c, fahrenheit_a[i]))>> 
-40.0 degrees Celsius = -40.0 degrees Fahrenheit 
-10.0 degrees Celsius = 14.0 degrees Fahrenheit 
0.0 degrees Celsius = 32.0 degrees Fahrenheit 
8.0 degrees Celsius = 46.0 degrees Fahrenheit 
15.0 degrees Celsius = 59.0 degrees Fahrenheit 
22.0 degrees Celsius = 72.0 degrees Fahrenhet 
38.0 degrees Celsius = 100.0 degrees Fahrenhet

Creating the model:

We will use the simplest model we can, a Dense network. For simplicity’s sake, this network will have only one layer and one neuron

Build a layer:

We’ll call the layer L1 and instantiate it using the syntax tf.keras.layers.Dense, with the following configurations:-

. input_shape=[1], this specifies that the input to this layer is a single value, that is the shape is a 1-dimensional array with 1 member.

. units = 1, this specifies the number of neurons in the layer. The number of neurons defines how many internal variables the model would have to try to learn to solve the problem

L1 = tf.keras.layer.Dense(units=1, input_shape=[1])

Assemble layers into the model:

Once layers are defined, we need to assemble them into our model. We shall use the Sequential model definition that takes in a list of layers as the argument. Specifying the calculation order from the input to output.

This model has just a single layer L1

tf.keras.Sequential([L1])

Note that we can build and assemble the layer in one line of code by simply doing:-

model= tf.keras.Sequential(tf.keras.layer.Dense(units=1, input_shape=[1]))

Compile the model with Loss and Optimizer function:

Before training, the model has to be compiled. When compiled, the model is given:

1. Loss Function: A way of measuring the difference between predictions and the desired outcome. (This difference is called the loss)

2. Optimizer Function: A way of adjusting internal values or parameters in a bid to reduce the loss.

model.compile(loss= 'mean_squared_error', optimizer= tf.keras.Optimizers.Adam(0.1))

In fact, the act of calculating the current loss and improving it is what training a model (model.fit) is all about.

During training, the optimizer function (in this case Adam Optimizer, which stands for Adaptive Moment Estimation optimizer) is used to calculate adjustments to the model’s internal parameters. For more details about optimizer algorithms, see this article.

TensorFlow uses numerical fine-tuning to adjust these parameters and all this complexity is hidden from us, so we will not go into those details here.

What’s important to know is this:-

The loss function (mean_squared_error) and the optimizer function (Adam) are standard for simple models like this one, but many others are available and it is not necessary to know how they work internally at this point.

In the code cell above there’s a 0.1 value passed to the Adam optimizer. That is the learning rate. The learning rate is simply the size the optimizer function takes when adjusting values within the model. If the learning rate is too small it takes too many iterations to optimize the model and if it’s too large, then accuracy goes down. Finding a good value often involves some trial and error, but it is usually between 0.001 (default) and 0.1.

Train the model:

We train the model by calling the fit() method.

During the training, the model takes in Celsius values and performs some calculation using the current internal variables(called weights), then outputs values which are meant to be the Fahrenheit equivalent.

Since the weights are initially set randomly, the output values will not be close to the correct values. The difference between the output values and desired outcomes will be calculated using the loss function, while the optimizer function determines how the weights should be adjusted to reduce the loss.

This cycle of calculate, compare, adjust is controlled by the fit() method.

history = model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False)print("Finished training the model")

The first argument to the fit() method is the input(Celcius values), the second argument is the desired output(Fahrenheit values), epochs specifies how many times the training should run and verbose controls how much data should be printed out when the training takes place. In this case, verbose=False means don’t print out any training data.

We save all these output parameters in a variable called history, so that we can call or access these internal values if the need arises, especially if we want to plot the training loss in real-time. Then we train the model.

Display training statistics:

The fit method returns a history object. we can use this object to plot how the loss of our model goes down after each training epoch.

Let’s visualize the training loss using the Matplotlib library.

import matplotlib.pyplot as plt
plt.xlabel('Epoch Number', color='yellow')
plt.ylabel("Loss Magnitude", color='yellow')
plt.plot(history.history['loss'])
plt.xticks(color='white')
plt.yticks(color='white')
plt.show()

Use the model to predict values:

Now that the model has been trained to learn the relationship or patterns between celsius_q and fahrenheit_a, we can use it to predict previously unknown Celsius to Fahrenheit degrees.

So for example, 200 degree Celsius to Fahrenheit as we already know is:-

200 * 1.8 + 32 = 392

Let’s run that using our trained model

model.predict([200])>>
 [[393.65097]]# Our model outputs 393.7, which is very close to the desired.

Let’s define a simple method that creates Celsius degrees and then we use our model to predict the Fahrenheit values of each one and we compare predictions to the desired values, print out these values and finally the Mean_Squared_Error.

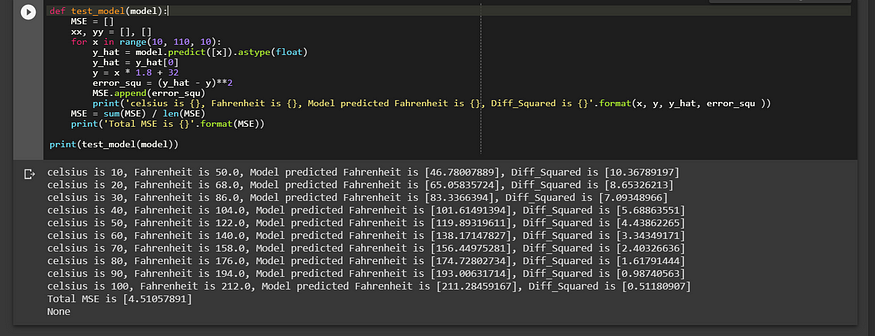
def test_model(model):
 MSE = []
 xx, yy = [], []
 for x in range(10, 110, 10):
 y_hat = model.predict([x]).astype(float)
 y_hat = y_hat[0]
 y = x * 1.8 + 32
 error_squ = (y_hat - y)**2
 MSE.append(error_squ)
 print('celsius is {}, Fahrenheit is {}, Model predicted Fahrenheit is {}, Diff_Squared is {}'.format(x, y, y_hat, error_squ ))
 MSE = sum(MSE) / len(MSE)
 print('Total MSE is {}'.format(MSE))print(test_model(model))>> 
See cell output below

To review:

1. We created a simple model with a Dense layer
2. We trained it with 3500 examples (7 pairs over 500 epochs)

Our model tuned the internal parameters(weights) in the Dense layer until it was able to return the correct Fahrenheit value for any Celsius value, even those not seen before, using the Loss and Optimizer functions.

Looking at the layer weights:

Finally, let’s print the internal parameters of the Dense layer

print('These are the internal layer variables{}'.format(L1.get_weights()))>>
This prints out:-
These are the internal layer variables: [array([[1.8278279]], dtype=float32), array([28.5018], dtype=float32)]

Notice that the first variable is 1.8, while the second is 28.5 which is relatively close to 32 (remember the formula for converting Celsius to Fahrenheit is Celsius times 1.8 plus 32)

Therefore for a neural network made up of a single neuron and a single input and a single output, the internal maths looks the same as the line formula AKA the Slope intercept form which is of the form:

y = mx + b

Which has the same form as the conversion formula we used above:-

Fahrenheit = 1.8*Celsius + 32

Since the form is the same, the variables should converge on the standard 1.8 and 32, which is what happened.

A little experiment…

Just for fun, let’s complicate things a little, let's add more Dense layers and more neurons, which would mean more internal variables to learn.

# First Dense layer
L1 = tf.keras.layer.Dense(units=4, input_shape=[1])
# Second Dense layer
L2 = tf.keras.layer.Dense(units=4)
# Third Dense Layer
L3 = tf.keras.layer.Dense(units=1)
# Let's assemble all the layers into a Sequential model
model = tf.keras.Sequential([L1, L2, L3])
# Let's compile the model
model.compile(loss='Mean_Squared_Error',Optimizer=tf.keras.optimizers.Adam(0.1))
# Let's train the model
model.fit(celsius_q, fahrenheit_a, epochs=500, verbose=False)
print("Finished training the model")
# Now let's print out the layer variables of each layer
print("These are the L1 variables: {}".format(L1.get_weights()))
print("These are the L2 variables: {}".format(L2.get_weights()))
print("These are the L3 variables: {}".format(L3.get_weights()))>>
Finished training the model 
These are the L1 variables: [array([[0.38865 , 0.16998766, 0.06720579, 0.38802674]], dtype=float32), array([ 3.093483 , 2.9697134, -2.297267 , 3.08295 ], dtype=float32)] 
These are the L2 variables: [array([[-0.61909986, -0.42321223, -0.12353817, -1.0181226 ], [-0.8338606 , -0.3931085 , -0.35709453, -0.02496582], [ 0.04785354, 0.83791655, 0.62090117, -0.35727897], [-1.0036206 , -0.4417855 , -0.26475334, -0.7752834 ]], dtype=float32), array([-2.9957104, -3.0123546, -2.1529603, -2.9795303], dtype=float32)] 
These are the L3 variables: [array([[-1.1074247 ], [-1.004997 ], [-0.512665 ], [-0.70594513]], dtype=float32), array([2.9236865], dtype=float32)]

We can clearly see that the internal layer variables are not in the slope-intercept form, but are more complex. This added complexity usually results in better prediction output, but the complex is not always better in all cases.

Let’s run the model one more time with our earlier defined test_model method to see if the added layers and neurons improved predictions,

print(test_model(model))>>
This prints out:- celsius is 10, Fahrenheit is 50.0, Model predicted Fahrenheit is [49.93202209], Diff_Squared is [0.004621] 
celsius is 20, Fahrenheit is 68.0, Model predicted Fahrenheit is [67.91150665], Diff_Squared is [0.00783107] 
celsius is 30, Fahrenheit is 86.0, Model predicted Fahrenheit is [85.89100647], Diff_Squared is [0.01187959] 
celsius is 40, Fahrenheit is 104.0, Model predicted Fahrenheit is [103.87049103], Diff_Squared is [0.01677257] 
celsius is 50, Fahrenheit is 122.0, Model predicted Fahrenheit is [121.84999084], Diff_Squared is [0.02250275] 
celsius is 60, Fahrenheit is 140.0, Model predicted Fahrenheit is [139.82948303], Diff_Squared is [0.02907604] 
celsius is 70, Fahrenheit is 158.0, Model predicted Fahrenheit is [157.80897522], Diff_Squared is [0.03649047] 
celsius is 80, Fahrenheit is 176.0, Model predicted Fahrenheit isonclusion[175.78848267], Diff_Squared is [0.04473958] 
celsius is 90, Fahrenheit is 194.0, Model predicted Fahrenheit is [193.76795959], Diff_Squared is [0.05384275] 
celsius is 100, Fahrenheit is 212.0, Model predicted Fahrenheit is [211.74746704], Diff_Squared is [0.0637729] 
Total MSE is [0.02915287]

We can see an amazing improvement.

The more complex model is 99.83% accurate with an MSE of only 0.03

Conclusion:

I hope I have been able to take you on a short but interesting introductory walk through the complexities and awesomeness of The TensorFlow machine learning and deep learning library. This is barely scratching the surface. But it’s enough to get you started.

You can find the code cells here on GitHub

But more importantly, go through this free course that covers all these topics in great detail at udacity.com

Cheers!

About Me:

Lawrence is a Data Specialist at Tech Layer, passionate about fair and explainable AI and Data Science. I hold both the Data Science Professional and Advanced Data Science Professional certifications from IBM. I have conducted several projects using ML and DL libraries, I love to code up my functions as much as possible even when existing libraries abound. Finally, I never stop learning and experimenting and yes, I hold several Data Science and AI certifications and I have written several highly recommended articles.

Feel free to find me on:-

Github

Linkedin

Twitter

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI