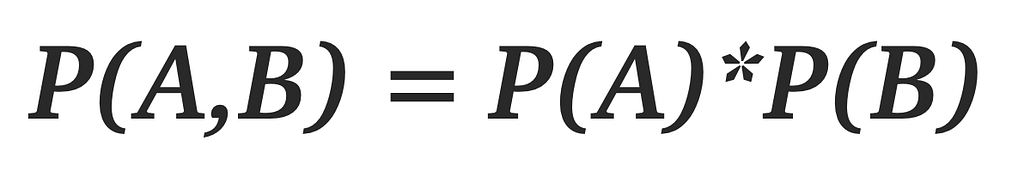
Conditional Independence

Author(s): Ampatishan Sivalingam

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

The independence that can be realized in the real world

When it comes to probability theory we all would have heard of joint distribution, marginal distribution, independence, etc. In this article, I will focus my attention on independence, especially conditional independence. If two events A and B are independent if they satisfy the following condition:

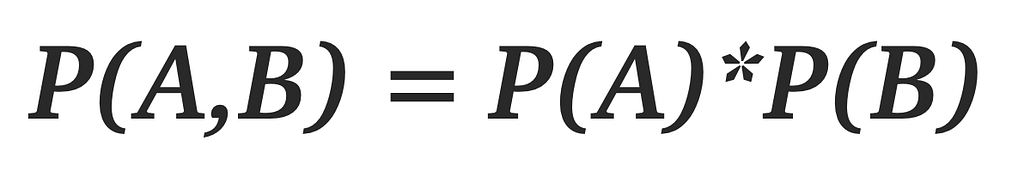
In others words, if the happening of event A doesn’t affect the probability of event B happening, both events are said to be independent. From the view of information theory, it can be interpreted as: if knowing A doesn’t provide any additional information about B, then A and B are said to be independent. These are the different interpretations of the concept of independence. There is a huge misunderstanding of thinking of mutually exclusive events as independent events, which is completely wrong. Earlier I also had this misconception, thinking if an event can’t happen if another event has already happened, then they both should be independent. But it's not true, like mentioned above for two events A and B to be independent, no information should be provided when A happens regarding the occurrence of B, but if A and B are mutually exclusive events, i.e A and B can’t occur at the same time. So if we know that A has happened then we are sure that B is not gonna happen, in other words, if we know that A happened it has all the information needed regarding the occurrence of B, which is completely opposite of the definition of independent events. Therefore, mutually exclusive events can never be independent events.

In the real world, realizing (unconditional) independence will be rare, because every event will be most likely influence other events, mostly these influences are directed through an intermediate event. So, if the occurrence of the intermediate event is realized, then there will be no other influence between the other two events, this concept is known as conditional independence, and can be observed in real-world scenarios. The formal definition for conditional independence is as follows:

Now we have dependence as well as conditional independence, now we will look if they two are related in any way.

1. Does independence imply conditional independence?

Consider two events A and B to be independent

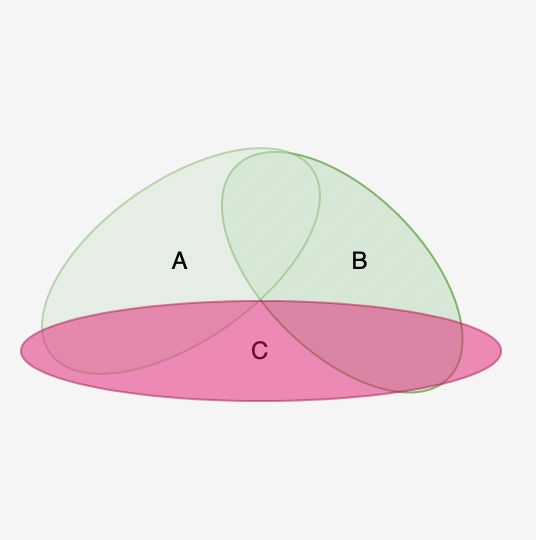
Now given a event C has occurred, the event A and B has become mutually exclusive event (both can’t happen at the same time), therefore not independent. So independence doesn’t implies conditional independence.

2. Does conditional independence implies independence

Consider we have two coins, one is biased and the other one is a fair coin, if we condition on choosing a fair coin or biased coin, then the coin flips will be independent of each other, on contrast if we don’t condition on a coin, then by looking at the outcomes for a certain period of time we can identify whether we have a biased coin or not, that will give us the information regarding the outcomes of the coin flips from other coin. So conditional independence doesn’t imply independence.

Conditional Independence was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI