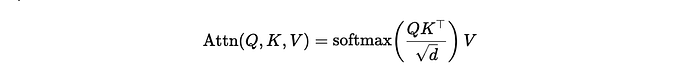Can Kolmogorov–Arnold Networks (KAN) beat MLPs?

Author(s): Vishal Rajput

Originally published on Towards AI.

Lately, it seems that the entire AI community has become about one and one thing only, LLMs. They are cool in their own way, but they are not the entire AI field. In all the LLMs and AI agent hype a paper like Kolmogorov–Arnold Networks is a breath of fresh air. This paper seems quite groundbreaking and might completely change the field. Rarely do we see papers challenging the fundamentals of AI, but this one seems to do it.

MLPs or Multi-layer perception sit at the very bottom of AI architectures. Dense layer (MLPs) is part of almost every Deep learning architecture. This paper directly challenges that foundation. Not only does it challenge the MLPs but also the black box nature of these models. So, in today’s blog, we are going to review this brand-new research paper.

Note: This is going to be quite math heavy article. Since this is fundamental research, it is important to understand the underlying maths of it.

Photo by Daniele Levis Pelusi on Unsplash

KAN: Kolmogorov-Arnold Networks introduces a new type of neural network architecture based on the Kolmogorov-Arnold representation theorem, presenting a promising alternative to traditional multi-layer perceptrons (MLPs).

According to the KAN paper:

While MLPs have fixed activation functions… Read the full blog for free on Medium.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI