How Do Language Models Predict the Next Word?🤔

Last Updated on December 28, 2020 by Editorial Team

Author(s): Bala Priya C 

N-gram language models – an introduction

Have you ever guessed what the next sentence in the paragraph you’re reading would likely talk about?

Have you ever noticed that while reading, you almost always know the next word in the sentence?

Well, the answer to these questions is definitely Yes! As humans, we’re bestowed with the ability to read, understand languages and interpret contexts, and can almost always predict the next word in a text, based on what we’ve read so far.

Can we make a machine learning model do the same?

Oh yeah! We very well can!

And we already use such models everyday, here are some cool examples.

In the context of Natural Language Processing, the task of predicting what word comes next is called Language Modeling.

Let’s take a simple example,

The students opened their _______.

What are the possible words that we can fill the blank with?

Books📗 📒📚

Notes📖

Laptops👩🏽‍💻

Minds💡🙂

Exams📑❔

Well, the list goes on.😊

Wait…why did we think of these words as the best choices, rather than ‘opened their Doors or Windows’? 🙄

It’s because we had the word students, and given the context ‘students’, the words such as books, notes and laptops seem more likely and therefore have a higher probability of occurrence than the words doors and windows.

Typically, this probability is what a language model aims at computing. Over the next few minutes, we’ll see the notion of n-grams, a very effective and popular traditional NLP technique, widely used before deep learning models became popular.

What does a language model do?

Describing in formal terms,

• Given a text corpus with vocabulary. V ,
• Given a sequence of words, x(1),x(2),…,x(t) ,
• A language model essentially computes the probability distribution of the next word. x(t+1) .

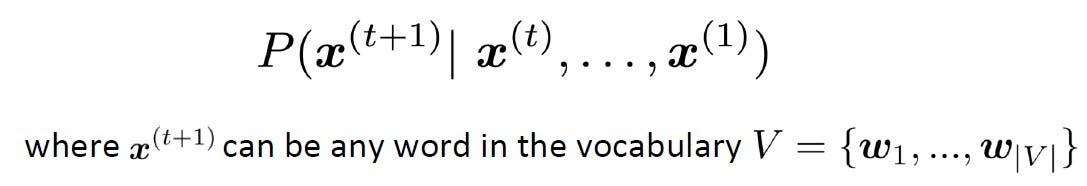
A language model, thus, assigns a probability to a piece of text. The probability can be expressed using the chain rule as the product of the following probabilities.

• Probability of the first word being x(1)
• Probability of the second word being x(2) given that the first word is x(1)
• Probability of the third word being x(3) given that the first two words are x(1) and x(2)
• In general, the conditional probability that x(i) is word i, given that the first (i-1) words are x(1),x(2),…,x(i-1)

The probability of the text according to the language model is:

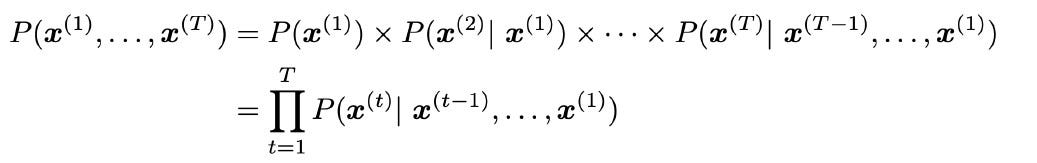
How do we learn a language model?

Learn n-grams! 😊

An n-gram is a chunk of n consecutive words.

For our example, The students opened their _______, the following are the n-grams for n=1,2,3 and 4

• unigrams: “the”, “students”, “opened”, ”their”
• bigrams: “the students”, “students opened”, “opened their”
• trigrams: “the students opened”, “students opened their”
• 4– grams: “the students opened their”

In an n-gram language model, we make an assumption that the word x(t+1) depends only on the previous (n-1) words. The idea is to collect how frequently the n-grams occur in our corpus and use it to predict the next word.

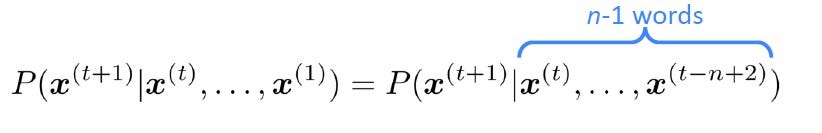
This equation, on applying the definition of conditional probability yields,

How do we compute these probabilities?

To compute the probabilities of these n-grams and n-1 grams, we just go ahead and start counting them in a large text corpus! The Probability of n-gram/Probability of (n-1) gram is given by:

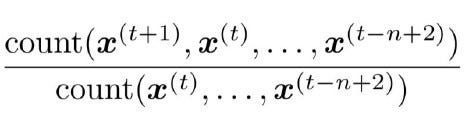
Let’s learn a 4-gram language model for the example,

As the proctor started the clock, the students opened their _____

In learning a 4-gram language model, the next word (the word that fills up the blank) depends only on the previous 3 words. If w is the word that goes into the blank, then we compute the conditional probability of the word w as follows:

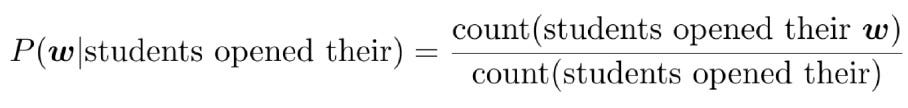
In the above example, let us say we have the following:

"students opened their" occurred 1000 times

"students opened their books" occurred 400 times
-> P(books/students opened their) = 0.4

"students opened their exams" occurred 200 times
-> P(exams/students opened their) = 0.2

The language model would predict the word books;

But given the context, is books really the right choice? Wouldn’t the word exams be a better fit?

Recall that we have,

As the proctor started the clock, the students opened their _____

Should we really have discarded the context ‘proctor’?🤔

Looks like we shouldn’t have.

This leads us to understand some of the problems associated with n-grams.

Disadvantages of the n-gram language model

Problems of Sparsity

What if “students opened their” never occurred in the corpus?

The count term in the denominator would go to zero!

• If the (n-1) gram never occurred in the corpus, then we cannot compute the probabilities. In that case, we may have to revert to using “opened their” instead of “students opened their”, and this strategy is called back-off.

What if “students opened their w” never occurred in the corpus?

The count term in the numerator would be zero!

• If word w never appeared after the n-1 gram, then we may have to add a small factor delta to the count that accounts for all words in the vocabulary V .This is called ‘smoothing’.

Sparsity problem increases with increasing n. In practice, n cannot be greater than 5

Problem of Storage

As we need to store count for all possible n-grams in the corpus, increasing n or increasing the size of the corpus, both tend to become storage-inefficient.

However, n-gram language models can also be used for text generation; a tutorial on generating text using such n-grams can be found in reference[2] given below.

In the next blog post, we shall see how Recurrent Neural Networks (RNNs) can be used to address some of the disadvantages of the n-gram language model.

Happy new year everyone! ✨

Wishing all of you a great year ahead! 🎉🎊🥳

References

[1] CS224n: Natural Language Processing with Deep Learning

[2] NLP for Hackers

---

How do language models predict the next word?🤔 was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI