Why Probability and Likelihood are not the Same Thing

Author(s): Towards AI Editorial Team

Originally published on Towards AI.

Understanding the crucial differences between Probability and Likelihood with examples

Author(s): Pratik Shukla

“The best way out is through”. — Robert Frost

Table of Contents:

1. Introduction
2. Introduction to probability and likelihood
3. Why is likelihood not a probability distribution?
4. The crucial differences between probability and likelihood
5. The difference between probability and likelihood question
6. Probability and likelihood for a binomial distribution
7. Conclusion
8. Resources and References

Introduction:

This blog explains the crucial differences between probability and likelihood. In our day-to-day lives using plain language, we use these terms interchangeably. However, there is an essential difference when used in the context of statistics and machine learning. This blog aims to explain those differences with theories and examples in an enjoyable and understandable way. Let’s dive into it!

Introduction to probability and likelihood:

In a cricket match, the captains of both teams are summoned to the field for a coin toss. The winning captain will choose to bat first, or bowl first based on the outcome of the coin toss.

Now, what is the probability that the winning captain will choose to bat first? We now know that there are only two conceivable outcomes: the winning captain decides to bowl first or start the batting. Therefore, there is a 50% chance that the victorious captain will choose to bat first.

The commentators are now debating the likelihood of the winning captain choosing to bat first inside the pavilion. As we already know, this number is not quite 50%. The likelihood that the winning captain will choose to bat first is affected by factors such as the pitch type, the weather, the opposing team, etc. We can say that if it has rained heavily just before the match, then the likelihood of the winning captain deciding to bat first might be as low as 1%. However, if the weather conditions are just perfect, then the likelihood of the winning captain choosing to bat first might be as high as 95%.

While calculating the probability value, we trust that the parameter value θ=0.5 is correct. After considering all the parameters, we assume we are sure about the parameter value θ=0.5. However, while calculating the likelihood, we are to find that parameter’s value. While calculating the likelihood, we aim to find whether we can trust the parameter or not.

So, we can say that probability is based on pure mathematics; however, likelihood is a function of many parameters and conditions.

Why is likelihood not a probability distribution?

We can state the following about the potential outcomes x in the case of a coin flip.

The probability that the coin lands a heads-up is,

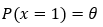
Now, based on that, we can state the following about finding the probability of a coin landing heads-up and tails-up.

The following equation can be used to generalize the previous set of equations.

Now, we can see that the above formula works just fine for the values of k=1 and k=0.

Now, we are going to consider two different circumstances.

1. CASE — 1: Probability

Let’s say before flipping the coin, we know the value of the parameter θ=3/4. Based on that, we can say that the probability of getting a head is P(heads) = θ = 3/4 and P(tails) = 1-θ = 1/4. Let’s plot this data on a simple graph.

Note: We are keeping the parameters (θ) constant and changing the data (x=1 or x=0).

2. CASE — 2: Likelihood

Now, let’s say we don’t know the probability of heads or tails before flipping the coin. Instead, we have the outcome of the data. Here, we have already flipped the coin and it turned out to be ahead. Now, what’s the probability of finding θ given x=1.

Note: In this case, we are keeping the data (x=1) constant and changing the parameter (θ).

We want to find the distribution that defines such an outcome. In short, we want to find the value of θ giving x. We can write it in a mathematical format as follows.

P(x=1 U+007C θ) = L(θ U+007C x=1)

Also, the critical thing to note here is that the area under the curve is 1/2. So, we can say that it is not a valid probability distribution. Instead, it is known as a likelihood distribution. Please note that the likelihood function does not obey the laws of probability. So, the likelihood function is not bound in the [0, 1] interval.

The crucial differences between probability and likelihood:

Let’s say we get a random variable X from a parameterized distribution F(X;θ). In this parameterized distribution, θ is the parameter that defines the distribution F(X;θ). Now, the probability of a random variable X=x would be P(X=x) = F(x;θ). Note that here the parameter θ is known.

However, we usually have the data (x) in the real world, and the parameter defining the distribution (θ) is unknown. Given the model F(X;θ), the likelihood is defined as the probability of observed data X as a function of θ. We can write that as L(θ) = P(θ; X=x). Here, X is known, but the parameter defining the distribution (θ) is unknown. In fact, the motivation for defining the likelihood is to determine the parameters of the distribution.

In our day-to-day lives, we often refer to probability and likelihood as the same thing. For example: What is the probability of rain tomorrow? Or how likely is it to rain tomorrow? However, these terms are widely different in machine learning and statistics. Let’s understand the crucial differences between probability and likelihood with the help of an example.

When we calculate the probability outcome, we assume that the parameters of our model are trustworthy. However, when we calculate the likelihood, we are trying to determine whether we can trust the parameters in the model or not based on the sample data we have observed.

Example: Coin Toss

What is a fair coin?
A coin is said to be a fair coin if the probability of it landing on heads and tails is the same. In other words, P(heads) = P(tails) = 1/2.

Let’s say we have a fair coin. Here, our assumption that the coin is fair is the parameter value (θ = 0.5). While finding probability, we assume that the parameters are trustworthy. Now, if we flip this coin once, the probability that it will land on heads up is 1/2. Now, let’s say that we flipped that coin a hundred times and found out that it landed on heads up only twelve times. Based on this evidence, we will say that the likelihood of that coin being fair is very low. If the coin were actually fair, we would expect it to land on heads up around half the times, i.e., 50 times.

In the above example, we can say that the coin landing on heads only twelve times out of hundred makes us highly suspicious that the actual probability of the coin landing on heads on a given toss is actually p = 0.5. But if the coin had landed fifty-five times on its head, we could say that the coin is likely to be fair.

The difference between probability and statistics questions:

Let’s say we are performing a coin toss. Now, consider the following two scenarios.

Probability Question:

Here, we are assuming that the coin is fair.

Question: What is the probability of getting two heads in a row?

It means what is the probability of observing the data (sequence) given the parameter values (P = 0.5).

Statistics Question:

Here, we don’t know whether the coin is fair or not. In fact, we are trying to determine the fairness of the coin. Now, let’s say we tossed the coin two times and got two heads in a row.

Question: Based on the observed data, what is the likelihood that the coin is fair? (P = 0.5)?

It means that we are trying to determine the value of parameters (P = 0.5) given the data (sequence = HH). In other words, we need to ask, “To what extent does our sample supports our hypothesis that P = 0.5?”

We can define likelihood as a measure of how strongly a sample supports a given value of a parameter in a parametric model.

Probability and likelihood for binomial distribution:

Let’s consider a straightforward case of binomial distribution where we are going to flip a coin ten times. Let’s say we flipped the coin ten times and recorded the outcomes. It turned out that we got nine heads and one tail.

CASE — 1:

We know that the coin is fair, i.e., p = 0.5. Based on that information, we want to find the probability of getting nine heads in ten flips. Here is the equation we can formulate.

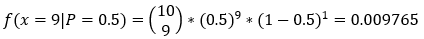
Here, 0.009765 is the probability of getting x = 9 heads given p = 0.5.

In a more general way, we can write the equation as follows:

CASE — 2:

Now, in this case, we are not sure whether the coin is fair. It means that we don’t know the value of the parameter P. Instead, we have tossed the coin ten times and have the toss results. It turned out that we got nine heads and one tail. So, based on that, we can say the following.

Here, we are trying to find the value of the parameter P based on the given sample of data (nine heads out of ten tosses).

Conclusion:

Probability refers to the chance that a particular outcome occurs based on the values specified by the parameters in a model. Here, we trust that the parameter values are accurate. On the other hand, likelihood refers to how strongly a sample supports a given parameter value in a parametric model. Therefore, we are attempting to determine the ideal parameter values for our model based on the provided sample data.

Citation:

For attribution in academic contexts, please cite this work as:

Shukla, et al., “Probability vs. Likelihood”, Towards AI, 2023

BibTex Citation:

@article{pratik_2023, 
 title={Probability vs. Likelihood}, 
 url={https://pub.towardsai.net/probability-vs-likelihood-a79335c985f7}, 
 journal={Towards AI}, 
 publisher={Towards AI Co.}, 
 author={Pratik, Shukla},
 editor={Binal, Dave}, 
 year={2023}, 
 month={Feb}
}

Resources and References:

1. Likelihood function — Wikipedia

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI