Linear Regression Complete Derivation With Mathematics Explained!

Last Updated on May 26, 2020 by Editorial Team

Author(s): Pratik Shukla

Machine Learning

Part 3/5 in Linear Regression

Part 1: Linear Regression From Scratch.

Part 2: Linear Regression Line Through Brute Force.

Part 3: Linear Regression Complete Derivation.

Part 4: Simple Linear Regression Implementation From Scratch.

Part 5: Simple Linear Regression Implementation Using Scikit-Learn.

In the last article, we saw how we could find the regression line using brute force. But that is not that fruitful for our data, which is usually in millions. So to tackle such datasets, we use python libraries, but such libraries are built on some logical theories, right? So let’s find out the logic behind some creepy looking formulas. Believe me, the math behind it is sexier!

Before we begin, the knowledge of the following topics might be helpful!

• Partial Derivatives
• Summations

Are you excited to find the line of best fit?

Let’s start by defining a few things

1) Given n inputs and outputs.

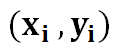
2) We define the line of best fit as:

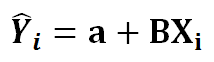
3) Now we need to minimize the error function we named S

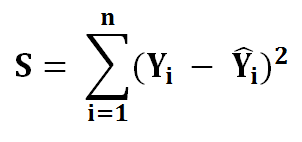
4) Put the value of equation 2 into equation 3.

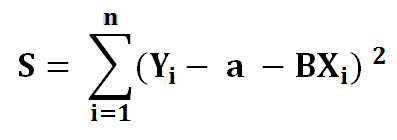
To minimize our error function, S, we must find where the first derivative of S is equal to 0 concerning a and b. The closer a and b are to 0, the less total error for each point is. Let’s find the partial derivative of a first.

Finding a :

1 ) Find the derivative of S concerning a.

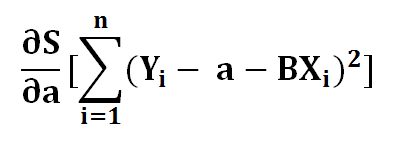
2 ) Using the chain rule, let’s say

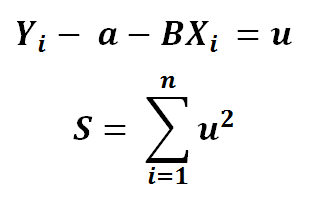
3) Using partial derivative

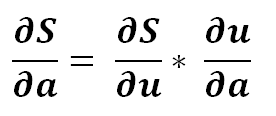
4) Expanding

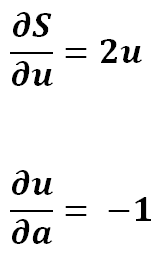
5) Simplifying

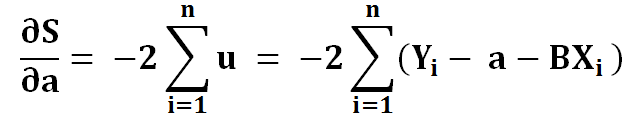
6) To find extreme values, we put it to zero

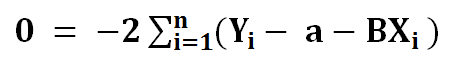
7) Dividing the left side with -2

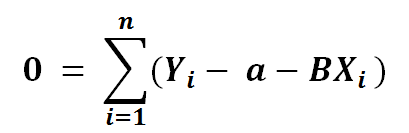
8) Now let’s break the summation in 3 parts

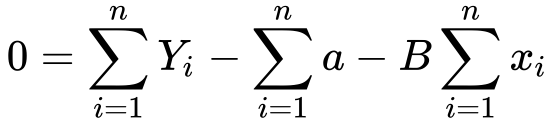
9) Now the summation of a is

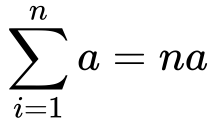
10) Substituting it back in the equation

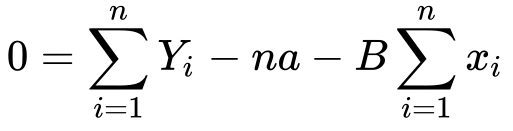
11) Now we need to solve for a

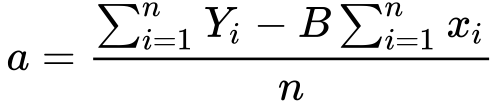
12) The summation of Y and x divided by n, is simply it’s mean

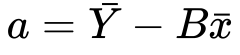
We’ve minimized the cost function concerning x. Now let’s find the last part which S concerning b.

Finding B :

1 ) Same as we have done with a

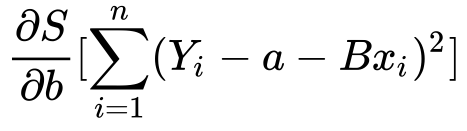
2) Finding the partial derivative

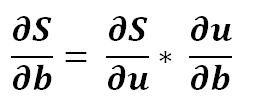
3) Expanding it a bit

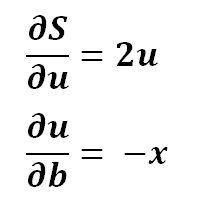
4) Putting it back in the equation

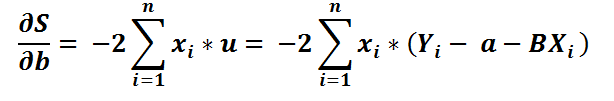
5) Let’s divide by -2 both sides

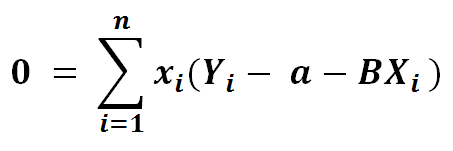
6) Let’s distribute x for ease of viewing

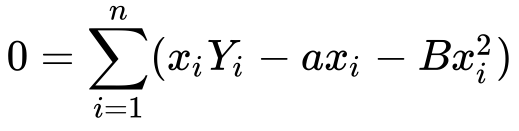
Now let’s do something fun! Remember, we found the value of earlier in this article? Why don’t we substitute it? Well, let’s see what happens.

7) Substituting the value of a

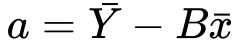
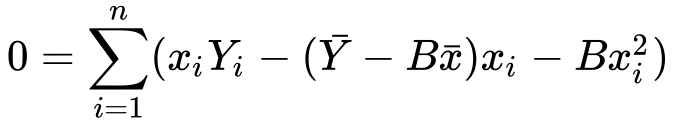
8) Let’s distribute the minus sign and x

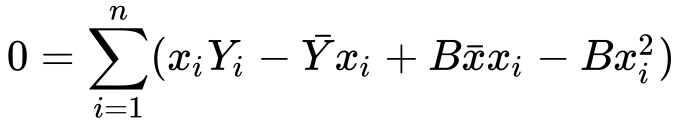
Well, you don’t like it? Let’s split up the sum into two sums

9) Splitting the sum

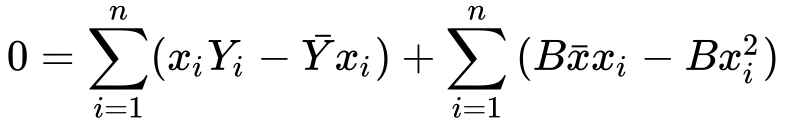
10) Simplifying

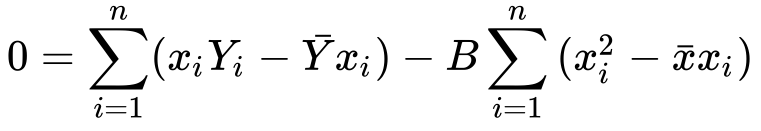
11) Finding B from it

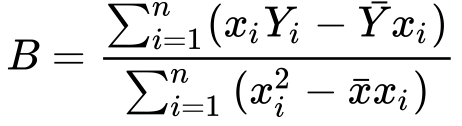
Great. We did it. We have isolated a and b in the form of x and y. It wasn’t that hard, was it?

I still have some energy and want to explore it a bit!

12 ) Simplifying the formula

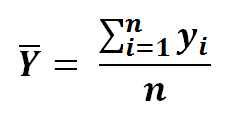
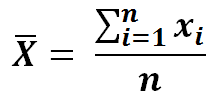
13) Multiplying numerator and denominator by n in equation 11

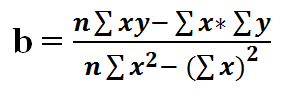
14) Now if we simplify the value of a using equation 13 we get

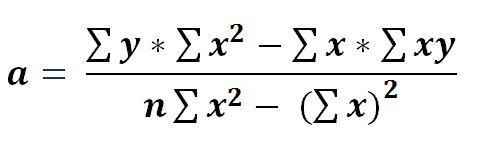
Summary 🙂

If you have a dataset with one independent variable, then you can find the line that best fits by calculating B.

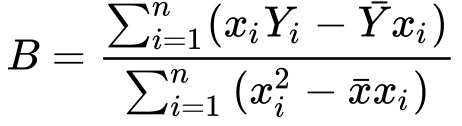
Then substituting B into a

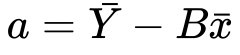
And finally substituting B and a into the line of best fit

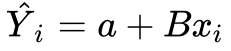
Moving Onwards,

In the next article, we’ll see how we can implement simple linear regression from scratch (without sklearn) in Python.

And please let me know whether you liked this article or not! I bet you liked it.

To find more such detailed explanation, visit my blog: patrickstar0110.blogspot.com

(1) Simple Linear Regression Explained With Its Derivation.

(2)How to Calculate The Accuracy Of A Model In Linear Regression From Scratch.

(3) Simple Linear Regression Using Sklearn.
You can download the code and some handwritten notes on the derivation on Google Drive.

If you have any additional questions, feel free to contact me: shuklapratik22@gmail.com.

---

Linear Regression Complete Derivation With Mathematics Explained! was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI

JOIN NOW!

Gain exclusive access to top AI tutorials, courses, and books to elevate your skills.

Get Access!

We won't send you spam. Unsubscribe at any time.