You Should Check Out This Effective Framework for Model Selection

Author(s): Andrew D #datascience

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

In every machine learning project, we will be faced with the need to select a model to start improving what our starting baseline is.

In fact, if the baseline gives us a useful starting model to understand what we can expect from a very simple solution, a model selected through a specific methodology helps us to move smoothly into the optimization phase of the project.

In this post, I will share with you my personal framework (and codebase) to conduct model selection in an organized and structured way.

The Method

Let’s say we have a regression problem to solve. Let’s start by importing the required libraries and configuring the logging mechanism

from sklearn import linear_model
from sklearn import ensemble
from sklearn import tree
from sklearn import svm
from sklearn import neighbors
from lightgbm import LGBMRegressor
from xgboost import XGBRegressor
import logging

logging.basicConfig(level=logging.INFO)

The mental model that I follow is the following:

1. we will create an empty list and populate it with the pair (model_name, model)
2. we will define the parameters for splitting the data through the Scikit-Learn KFold cross-validation
3. we will create a for loop where we will cross-validate each model and save its performance
4. we will view the performance of each model in order to choose the one that performed best
5. We define a list and insert the models we want to test.

Let’s define a list and insert the models we want to test.

models = []
models.append(('Lasso', linear_model.Lasso()))
models.append(('Ridge', linear_model.Ridge()))
models.append(('EN', linear_model.ElasticNet()))
models.append(('RandomForest', ensemble.RandomForestRegressor()))
models.append(('KNR', neighbors.KNeighborsRegressor()))
models.append(('DT', tree.DecisionTreeRegressor()))
models.append(('ET', tree.ExtraTreeRegressor()))
models.append(('LGBM', LGBMRegressor()))
models.append(('XGB', XGBRegressor()))
models.append(('GBM', ensemble.GradientBoostingRegressor()))
models.append(("SVR", svm.LinearSVR()))

For each model belonging to the model's list, we will evaluate its performance through model_selection.KFold. The way it works is rather simple: our training dataset (X_train, y_train) will be divided into equal parts (called folds), which will be tested individually. Hence, KFold cross-validation will provide an average performance metric for each split rather than a single metric based on the entire training dataset. This technique is very useful because it allows you to measure the performance of a model more accurately.

Since this is a regression problem, we will use the mean squared error (MSE) metric.

Let’s define the parameters for the cross-validation and initialize the for a loop.

n_folds = 5 # number of splits 
results = [] # save the performances in this list
names = [] # this list helps us save the model names for visualization

# we begin the loop where we'll test each model in the models list
for name, model in models:
    kfold = model_selection.KFold(n_splits=n_folds)
    logging.INFO("Testing model:", name)

    cv_results = model_selection.cross_val_score(
        model, # the model picked from the list
        X_train, # feature train set
        y_train, # target train set
        cv=kfold, # current split
        scoring="neg_mean_squared_error", 
        verbose=0, 
        n_jobs=-1)

    results.append(cv_results)
    names.append(name)

    msg = "%s: %f (%f)" % (name, cv_results.mean(), cv_results.std())

    logging.INFO(msg+"n")

Each model will be cross-validated, tested, and its performance saved in the results.

The visualization is very simple and will be done through a boxplot.

# Compare our models in a box plot
fig = plt.figure(figsize=(12,7))
fig.suptitle('Algorithm Comparison')
ax = fig.add_subplot(111)
plt.boxplot(results)
ax.set_xticklabels(names)
plt.show()

The Final Result

The final result will be this:

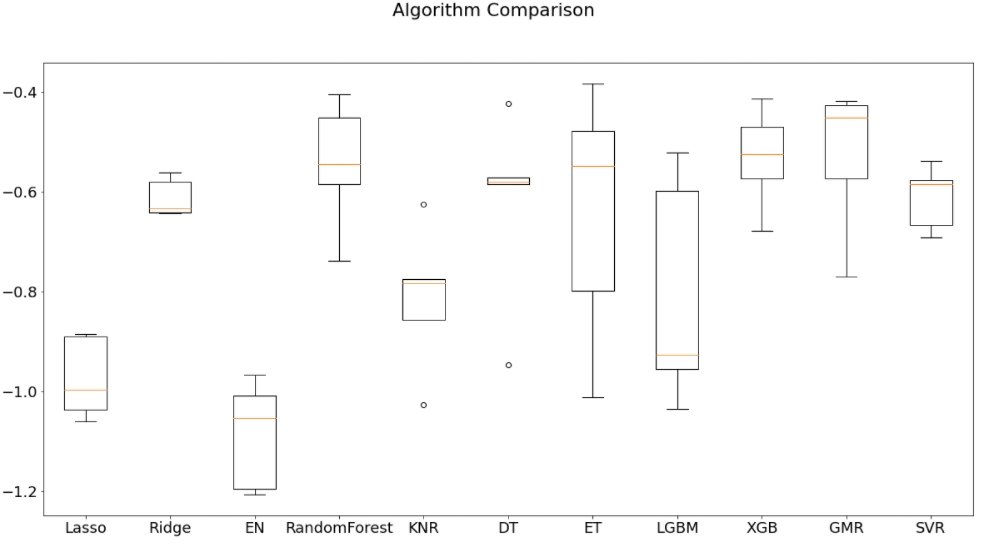
From here, you can see how RandomForest and GradientBoostingMachine are the best performing models. We can then start creating new experiments and further testing these two models.

Putting It All Together

Here’s the copy-paste template for model selection, which I would conveniently use in a model_selection.py script (I talk about how structuring a machine learning project here)

Conclusion

Glad you made it here. Hopefully, you’ll find this article useful and implement snippets of it in your codebase.

If you want to support my content creation activity, feel free to follow my referral link below and join Medium’s membership program. I will receive a portion of your investment, and you’ll be able to access Medium’s plethora of articles on data science and more in a seamless way.

Join Medium with my referral link – Andrew D #datascience

Have a great day. Stay well 👋

---

You Should Check Out This Effective Framework for Model Selection was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI