Statistics 101- Part 2- Probability Distributions, Types, and Applications

Author(s): Kumar kaushal

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Definition of the probability distribution, different types of distributions, their explanation, and applications

This article is in continuation of Statistics 101-Part 1 article. Here, we will discuss probability distributions, their types, and applications. Probability distributions are building blocks of business decisions based on statistical analysis, machine learning, and others. Hence, understanding the concepts related to probability distribution is vital.

Contents

• Probability distribution definition and important concepts
• Types of probability distributions
• Choosing the right distribution
• Applications

Probability distribution definition and important concepts

The probability distribution is related to frequency distribution. When actually conducting an experiment and observing frequencies of all outcomes, it is called frequency distribution. Whereas, when we list probabilities of all possible outcomes that could take place if an experiment was done, it is called probability distribution.

let us suppose that we have some number of defects and their probability of happening recorded as shown in the below table:

The probability distribution of the above example would be as shown here:

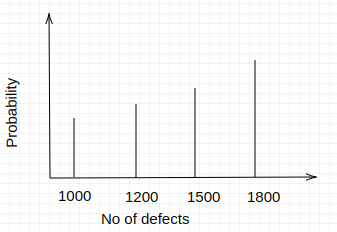
Another important concept to know is Random Variables. Random variables are variables that are assigned different values basis a random experiment. It changes from occurrence to occurrence with no pattern that can be predicted.

Types of probability distributions

We can broadly classify probability distributions into two categories- discrete probability distribution and continuous probability distribution.

Discrete probability distribution

If we are considering discrete variables in the probability distribution, then it would be a discrete probability distribution, and the values taken are only a few possible values. For example, the probability of the outcome of a number in a dice would be a discrete probability because outcomes can only have six possible values. A function defining a discrete probability distribution is called a Probability Mass Function (PMF).

A Binomial Distribution is an example of a discrete probability distribution for a discrete random variable. It is defined as shown below:

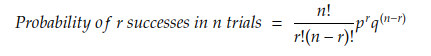
where p=probabilty of success, q=1-p=probability of failure, r = number of success required, and n= number of trials. Conditions for using a Binomial distribution are mentioned below:

• Each trial should have only two outcomes ( example- yes or no, pass or fail)
• The probability of the outcome of a trial remains constant over time. For example, the probability of a head in a fair coin’s toss will be constant, i.e., 0.5
• The trials are independent of each other, i.e., the outcome of a trial will not depend on the outcome of another trial.

Another well-known discrete probability distribution is the Poisson distribution. This distribution is defined as per the below equation:

where lambda= mean number of occurrences per interval

If we are interested in knowing the probability of x occurrences, the below conditions should be met in the case of Poisson distribution:

• The probability of exactly one occurrence in one interval is a very small number and is constant
• The probability of two or more occurrences in one interval can be assigned a zero value
• The number of occurrences per interval is independent of time
• The number of occurrences per interval is independent of the number of occurrences in other time intervals.

Another example of the discrete probability distribution is the discrete uniform distribution.

Continuous probability distribution

Variables considered under continuous probability distribution can take any value within a range of values. For example, the probability distribution of heights of a region’s population would be a continuous probability distribution, as heights a person can take any value.

A function defining a continuous probability distribution is called a Probability Density Function (PDF). A well know continuous probability distribution is a Gaussian distribution, also referred to as a Normal distribution.

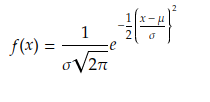
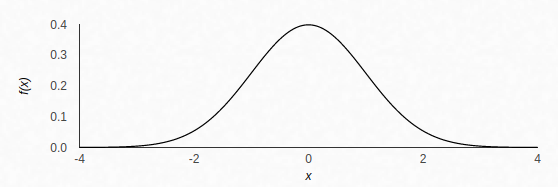
The normal distribution should have the following characteristics:

• The distribution should be unimodal i.e., it must have only a single peak
• The mean for the curve should be centered
• Mean should be equal to mode and median
• The two tails of the distribution should extend indefinitely and never touch the horizontal axis

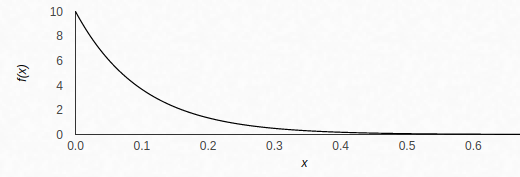
An exponential distribution is defined as per the below equation:

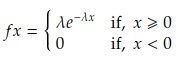
where lambda is called a rate parameter

In the first article of this series, we have seen the case of t-distribution, also known as Student’s distribution. This distribution is used in cases where the sample size is less than 30, and the population standard deviation is not known. Like a normal distribution, this distribution, too, is symmetrical but is a bit flatter than a normal distribution. There are different t-distributions for every possible sample size, depending on the degrees of freedom. As the sample size increases, it becomes close to a normal distribution.

Examples of other continuous probability distributions are log-normal, continuous uniform, Chi-Square distribution, and others.

Choosing the right distribution

It is critical that the right distribution is selected for the application. We must be able to categorize if the distribution to be used is discrete or continuous and, subsequently, if condition(s) for a specific distribution is being met. For example, in order to be able to use a Binomial distribution, the conditions listed in the section on “types of probability distributions- Discrete probability distribution” must be met. Similarly, if we want to use a normal distribution, the conditions for such distribution must be met.

Applications

Probability distributions are widely used in various applications. We have to understand the use case and the prevailing conditions to apply a specific distribution and arrive at the probability of an event of interest.

If a business manager is attempting to estimate the probability of x number of defects from a pool of n components, this may be a use case of Binomial distribution.

If a clinic’s manager wants to calculate the number of patient arrivals in a day, Poisson distribution may be used for this case.

The income distribution of a country can be represented as a normal distribution, provided meeting the required conditions.

We can use Chi-Square distribution in scenarios where we want to test the independence of two parameters, such as marital status and education level, or gender and salary.

Hence, there are numerous examples to show that probability distributions can be applied for specific usages.

Follow me (kumarkaushal.bit) for more interesting topics related to Data Science and Statistics.

---

Statistics 101- Part 2- Probability Distributions, Types, and Applications was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI