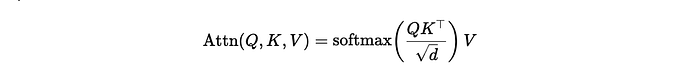Solving SUDOKU with Binary Integer Linear Programming(BILP)

Author(s): Harjot Kaur

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Background

Sudoku is a logic-based puzzle that first appeared in the U.S. under the title “Number Place” in 1979 in the magazine Dell Pencil Puzzles & Word Games [6]. The game was designed by Howard Garns, an architect who, upon retirement, turned to puzzle creation. In the 1980s, the game grew in popularity in Japan and was renamed by publisher Nikoli to “suji wa dokushin ni kagiru,” which translates as “the digits must remain single.” This was eventually shortened to “sudoku” or “single number.”

Heads up — assuming readers already know the basics of Linear Programming

Is Sudoku an optimization problem?

No. Mostly not. Because there is no objective function we want to maximize or minimize. The sudoku problem can be called a satisfiability or feasibility problem.

Let’s begin with the rules…

Sudoku most commonly appears in its 9 ×9 matrix form. The rules are simple: fill in the matrix so that every row, column, and 3 ×3 submatrix contains the digits 1 through 9 exactly once. Each puzzle appears with a certain number of givens. The number and location of these determine the game’s level of difficulty.

As we know, each ILP problem is composed of an objective function(not applicable in the case of Sudoku unless there are alternate solutions), decision variables, and constraints.

The good news is that we don’t write constraints for this, we just mathematically put up the rules of the puzzle as constraints!

Integer Programming mathematical model of the Sudoku puzzle

For ease of explanation, I’ll be using a 4×4 matrix up ahead. Let us consider the following puzzle to be solved using BILP.

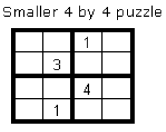
More specifically, we will formulate a binary integer program (BILP) for a general n×n puzzle. Once the program is developed to solve the BILP for Figure 1, it can be easily adapted to solve any Sudoku puzzle.

To begin, we define our decision variables:

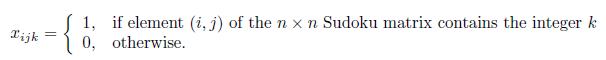
When the values of the decision variables are determined, we will know whether each integer k(1 ≤k≤4) appears in each element (i, j) of the n×n Sudoku matrix. That is, the solution to the corresponding Sudoku puzzle will be defined.

We now turn to the ever-important objective function and set of constraints. Notice how the constraints require only a knowledge of the rules of Sudoku puzzles (with the addition of one implicit constraint, which is a constraint (6) below) and do not require a proficiency with the logic necessary to solve such puzzles by hand. A BILP formulation suitable for Sudoku puzzles is as follows:

Min 0 (let us define this as a constant, as there is no function to minimize or maximize)

Subject to

Constraint 1: Each cell contains a single integer k

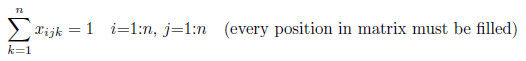
Constraint 2: Each integer k appears once in each row

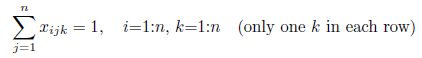
Constraint 3: Each integer k appears once in each column

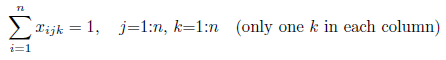
Constraint 4: Each integer k appears once in each submatrix

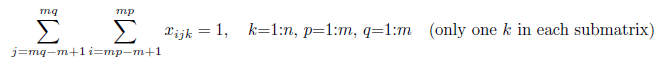
Constraint 5: Given elements G in the matrix are set “on”

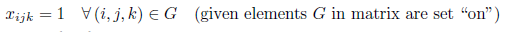
Constraint 6: Defining the possible value of integers

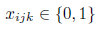
And, that’s that!

Let’s solve the above 4×4 Sudoku puzzle(Figure1) using the Excel Solver. The simulation template for a 4×4 puzzle with 64 binary decision variables will look something like this.

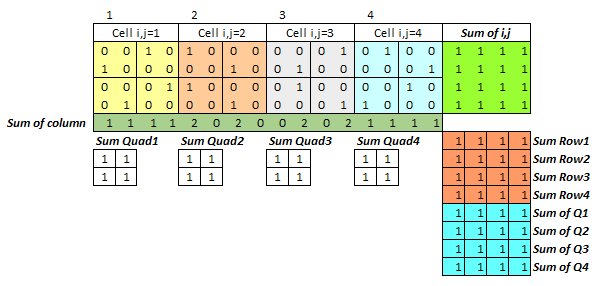
Now, let’s interpret the aforementioned constraints:

Constraint 1: Each cell contains a single integer k. Tabs colored in green(Sum of i,j = 1) will make sure that every position is filled with an integer value.

Constraint 2: Each integer k appears once in each row. Tabs colored in brick red(Sum of row 1:4 >= 1) will ensure that each k appears just once in every row.

Constraint 3: Each integer k appears once in each column. Tabs colored in olive (Sum of column 1:16 >= 1) will ensure that each k appears just once in every column.

Constraint 4: Each integer k appears once in each submatrix. Tabs colored in turquoise(Sum of quadrant 1:4 >= 1) will ensure that each k appears just once in every 2×2 matrix.

Constraint 5: Given elements G in the matrix are set “on”. The given value of k is hard coded.

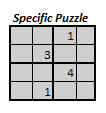
The last step is to convert the Integer Program solution as given in the 64 yellow, peach, grey and blue decision variable cells to the required 4 by 4 Sudoku grid. Each binary cell is then multiplied by the possible set of values a “k” can take(which is {1,2,3,4}).

Now let’s get the solution…

This is how the Excel Solver shall look like

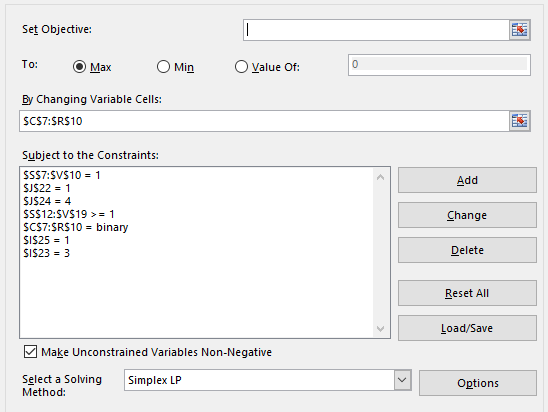
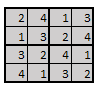
…and Voila! The solution to the 4×4 puzzle shall look like this.

Last words

The above logic can be used not just to solve any Sudoku puzzle but also to create one. I hope, you folks found it easy to grasp and fun too! Connect with me on Linkedin to talk more about optimization.

---

Solving SUDOKU with Binary Integer Linear Programming(BILP) was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI