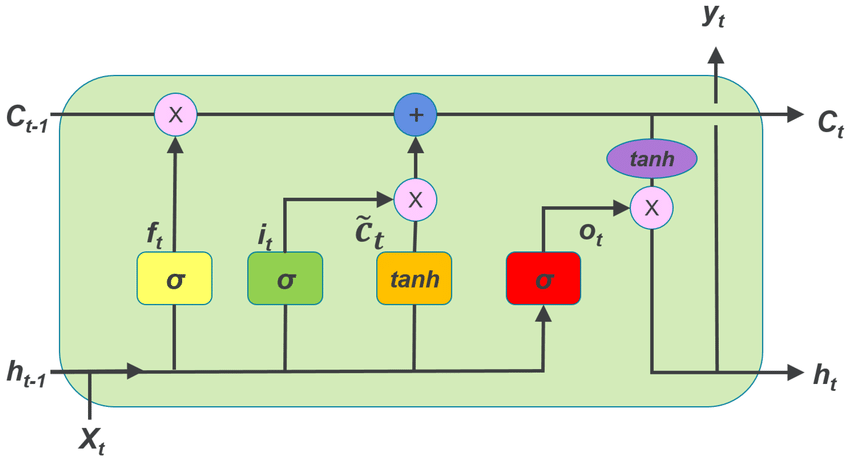
PyTorch LSTMCell — Shapes of Input, Hidden State, Cell State And Output

Author(s): Sujeeth Kumaravel

Originally published on Towards AI.

In Pytorch, to use an LSTMCell (with nn.LSTMCell), we need to understand how the tensors representing the input time series, hidden state vector, and cell state vector should be shaped. In this article, let us assume you are working with multivariate time series. Each multivariate time series in the dataset contains multiple univariate time series.

In this article, we use the following terminology,

batch = number of multivariate time series in a single batch from the dataset

input_features = number of univariate time series in one multivariate time series

time_steps = number of time steps in each multivariate time series

The batch of multivariate time series from which input to the LSTMCell is given should be a tensor of shape (time_steps, batch, input_features)

The following picture gives an understanding of this shape for input:

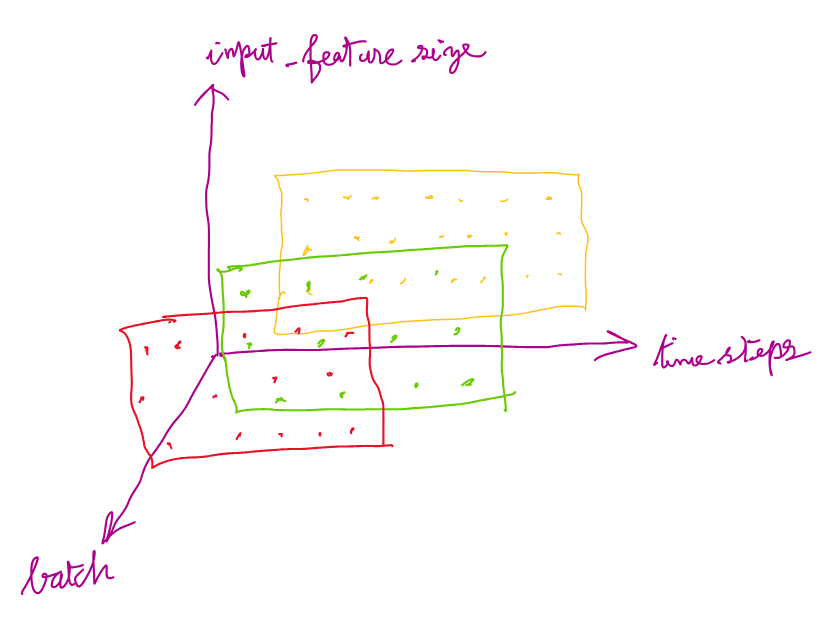
Input to an LSTMCell is given in a specific way. Basically, the entire multivariate time series is not given as input as a time series. The vector x_t, which is the vector at a specific time step in the MTS, is given as input to the LSTMCell. For processing a single time step’s vector, the LSTMCell needs a single hidden state vector as part of the input and a single cell state vector as part of the input. These are represented as h_0 and c_0, respectively. The output of the LSTMCell will be the hidden state and cell state that will be used while processing the input vector at the next time instance x_t+1. These hidden and cell states are represented as h_1 and c_1 respectively. The LSTMCell is called in a loop, passing in h_1 and c_1 as h_0 and c_0 for subsequent time steps. This concept is illustrated in the following code snippet.

While initializing an LSTMCell object, the arguments input_features, and hidden_size should be given.

Here,

input_features = number of univariate time series in one multivariate time series (same value as input_features mentioned above)

hidden_size = number of dimensions in the hidden state vector. This same size should be used for a number of dimensions in the cell state vector as well.

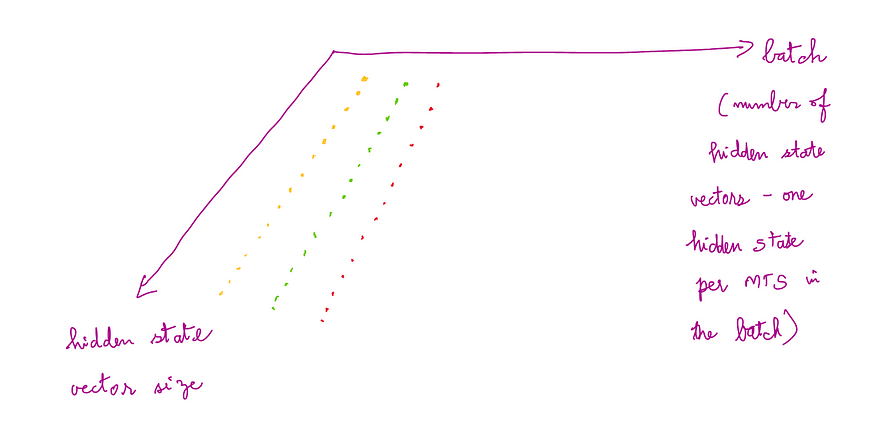
The initial values of the hidden state and cell state in the LSTMCell should be created with shape (batch, hidden_size). Here, the batch should match the batch in the input multivariate time series. This means, for each MTS in the input batch, there is a corresponding hidden_state and cell_state.

The time series the initial hidden state and the initial cell state should be given as input for a forward propagation through the LSTMCell.

The forward propagation of a specific time step’s vector of the input MTS, initial hidden state and initial cell state through the LSTMCell object should be in the format:

LSTMCell(x_t, (h_0, c_0))

The following picture gives an understanding of this shape for the hidden state and cell state:

An example code is given below. An explanation of the code follows.

import torch
import torch.nn as nn 

lstm_0 = nn.LSTMCell(10, 20) # (input_features, hidden_size)
inp = torch.randn(7, 3, 10) # (time_steps, batch, input_features) -> input time series
hx = torch.randn(3, 20) # (batch, hidden_size) -> initial value of hidden state
cx = torch.randn(3, 20) # (batch, hidden_size) -> initial value of cell state

for i in range(inp.size()[0]):
 hx, cx = lstm_0(inp[i], (hx, cx)) # forward propogation of input through LSTMCell
 output.append(hx)

output = torch.stack(output, dim=0)

Calling nn.LSTMCell() will call the __init__() dunder magic method and create an LSTMCell object. In the code above this object is referenced as lstm_0.

In RNNs in general (LSTM is a type of RNN), each time_step of the input time series should be passed into the RNN one at a time in a sequence order to be processed by the RNN.

In order to process multivariate time series in a batch using an LSTMCell, each time_step in all MTSs in the batch should be passed through the LSTMCell sequentially.

This is achieved by the for loop. The loop iterates over each time_step of the MTS (the first dimension of inp.size() is the number of time_steps) and passes the time_step’s vector in each MTS in the batch parallelly into the LSTMCell. A single call to the LSTMCell processes only one time_step’s vector in the MTS.

The output of the call lstm_0(inp[i], (hx, cx)) inside the for loop is the creation of the next hidden_state and cell state for each time_step. The output hidden_state (hx) and cell_state (cx) recursively get calculated based on the previous hx and cx.

Output: (h_1, c_1)

This output is computed for each time series across the entire batch. The output shape is (batch, hidden_size).

The following picture gives an understanding of the shape of the hidden state and cell state which are output:

These calculated hx that get created for each time step in each MTS in the input batch are appended in the output tensor, which in turn is stacked along the 0 axis. Hence, the output has the dimensions (time_steps, batch, hidden_size).

For the above code example, the following is the output:

tensor([[[ 0.0087, 0.0365, -0.1233, -0.2641, 0.2908, -0.5075, 0.2587,
 0.1057, -0.2079, -0.2327, 0.1390, 0.1023, -0.1186, 0.3302,
 0.1139, 0.1591, -0.0264, -0.0499, 0.0153, 0.3881],
 [ 0.3585, -0.4133, -0.0259, 0.2490, -0.0936, -0.2756, -0.1941,
 -0.0967, 0.1501, -0.0334, -0.1904, -0.3945, -0.1036, -0.2091,
 0.0545, 0.1937, -0.2338, 0.0382, 0.2344, 0.1169],
 [-0.2532, 0.0745, -0.0329, 0.0971, -0.1057, -0.0383, 0.1328,
 0.1263, -0.1422, 0.0351, 0.3957, -0.4115, -0.2951, -0.5560,
 0.1941, 0.0100, 0.3028, -0.1803, 0.0028, 0.3210]],

 [[ 0.1105, -0.1295, -0.0636, -0.2510, 0.1923, -0.2457, 0.2401,
 0.1379, -0.1373, -0.2451, 0.0387, 0.1004, -0.0580, 0.3430,
 -0.0149, 0.1827, -0.0229, -0.2061, 0.1718, 0.3146],
 [ 0.2741, -0.2413, -0.1310, 0.1206, 0.0379, -0.1738, -0.0568,
 0.0417, 0.0756, 0.1020, 0.0262, -0.3280, -0.0352, -0.1713,
 0.1065, 0.0458, -0.3404, -0.0795, 0.0586, 0.0026],
 [-0.0112, 0.0883, -0.1755, -0.0438, 0.0193, 0.0151, 0.1010,
 0.1614, -0.0524, 0.0970, 0.2092, -0.3518, -0.0715, -0.3941,
 0.1422, 0.1164, 0.2946, -0.1919, 0.1493, 0.1203]]],
 grad_fn=<StackBackward0>)

For each time step in the input (time_steps in the input = 2) an array is created (2 arrays are created). Each of these arrays contains arrays for each MTS in the batch (batch_size = 3). For each time_step in the MTS, we get a hidden state vector output of hidden_size dimension (here hidden_size = 20). So, for each time step, the MTS value is a vector. This vector at a time_step gets mapped into a 20-dimensional hidden_state vector.

The following picture gives an understanding of this shape for output multivariate time series batch:

If you print hx in the code above for one time step (for one iteration in the loop), the following is the output:

tensor([[ 0.1034, -0.0192, -0.0581, -0.0772, -0.1578, -0.1450, 0.0377, -0.0013,
 -0.2641, -0.1821, 0.0431, -0.2262, 0.3025, 0.0952, 0.4113, -0.2968,
 -0.4377, 0.0794, 0.3683, -0.0021],
 [ 0.0309, 0.3957, 0.2143, 0.1020, 0.0640, -0.0628, 0.4390, 0.1818,
 0.0373, 0.2497, -0.1768, -0.2038, -0.1249, -0.2995, 0.0786, -0.0522,
 -0.0080, -0.3095, -0.0815, 0.2874],
 [-0.2458, 0.1622, 0.2564, -0.3136, 0.0631, 0.0643, 0.4036, 0.3293,
 -0.1806, -0.0251, -0.4505, -0.1437, -0.1718, -0.0479, -0.1116, -0.1065,
 -0.3289, 0.1137, 0.1160, 0.1227]], grad_fn=<MulBackward0>)

It has one array corresponding to one-time step. Inside this time_step, there are 3 arrays, corresponding to 3 MTS in the batch. Each of these arrays corresponding to one MTS has a 20-dimensional hidden vector. So, the output in one time_step is (batch, hidden_size).

This output size can be understood using the following picture:

nn.LSTMCell’s initialization arguments are:

input_size

hidden_size

bias

device

dtype

It doesn’t have num_layers. Since this is a single cell, it cannot have multiple LSTM layers.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI