
Outlier Detection (Part 2): Multivariate
Last Updated on July 24, 2023 by Editorial Team
Author(s): Mishtert T
Originally published on Towards AI.

Analyze even better — For Better Informed Decision
Mahalanobis distance U+007C Robust estimates (MCD): Example in R

In Part 1 (outlier detection: univariate), we learned how to use robust methods to detect univariate outliers. This part we’ll see how we can better identify multivariate outlier.
Multivariate Statistics — Simultaneous observation and analysis of more than one outcome variable
We’re going to use “Animals ”data from the “MASS” package in R for demonstration.

The variables for the demonstration are body weight and brain weight of Animals which are converted to its log form (to make highly skewed distributions less skewed)
Y <- data.frame(body = log(Animals$body), brain = log(Animals$brain))plot_fig <- ggplot(Y, aes(x = body, y = brain)) + geom_point(size = 5) +
xlab("log(body)") + ylab("log(brain)") + ylim(-5, 15) +
scale_x_continuous(limits = c(-10, 16), breaks = seq(-15, 15, 5))

Before getting into how of the analysis part. Let’s try and understand some basics.
Mahalanobis distance
Mahalanobis (or generalized) distance for observation is the distance from this observation to the center, taking into account the covariance matrix.

- Classical Mahalanobis distances: sample mean as estimate for location and sample covariance matrix as estimate for scatter.
- To detect multivariate outliers the Mahalanobis distance is compared with a cut-off value, which is derived from the chi-square distribution
- In two dimensions we can construct corresponding 97.5% tolerance ellipsoid, which is defined by those observations whose Mahalanobis distance does not exceed the cut-off value.
Y_center <- colMeans(Y)
Y_cov <- cov(Y)
Y_radius <- sqrt(qchisq(0.975, df = ncol(Y)))library(car)
Y_ellipse <- data.frame(ellipse(center = Y_center,
shape = Y_cov,radius = Y_radius, segments = 100, draw = FALSE))
colnames(Y_ellipse) <- colnames(Y)plot_fig <- plot_fig +
geom_polygon(data=Y_ellipse, color = "dodgerblue",
fill = "dodgerblue", alpha = 0.2) +
geom_point(aes(x = Y_center[1], y = Y_center[2]),
color = "blue", size = 6)
plot_fig

The above method gives us 3 potential outlier observations, which are close to the ellipse line.
Is this robust enough? Or would we see a few more outliers if we use a different method?
Robust estimates of location and scatter
Minimum Covariance Determinant (MCD) estimator of Rousseeuw is a popular robust estimator of multivariate location and scatter.
- MCD looks for those h observations whose classical covariance matrix has the lowest possible determinant.
- MCD estimate of location is then mean of these h observations
- MCD estimate of scatter is a sample covariance matrix of these h points (multiplied by consistency factor).
- The re-weighting step is applied to improve efficiency at normal data.
- The computation of MCD is difficult, but several fast algorithms are proposed.
Robust estimates of location and scatter using MCD
library(robustbase)
Y_mcd <- covMcd(Y)
# Robust estimate of location
Y_mcd$center
# Robust estimate of scatter
Y_mcd$cov
By plugging in these robust estimates of location and scatter in the definition of the Mahalanobis distances, we obtain robust distances and can create a robust tolerance ellipsoid (RTE).
Robust Tolerance Ellipsoid: Animals
Y_mcd <- covMcd(Y)ellipse_mcd <- data.frame(ellipse(center = Y_mcd$center,
shape = Y_mcd$cov,
radius= Y_radius,
segments=100,draw=FALSE))colnames(ellipse_mcd) <- colnames(Y)plot_fig <- plot_fig +
geom_polygon(data=ellipse_mcd, color="red", fill="red",
alpha=0.3) +
geom_point(aes(x = Y_mcd$center[1], y = Y_mcd$center[2]),
color = "red", size = 6)
plot_fig

Distance-Distance plot
The distance-distance plot shows the robust distance of each observation versus its classical Mahalanobis distance, obtained immediately from MCD object.
plot(Y_mcd, which = "dd")

Check outliers
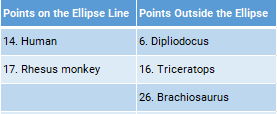
Summary
Minimum Covariance Determinant estimates plugged with Mahalanobis distance provide us better detection capability of outliers than our classical methods.
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














