Mathematics Behind Support Vector Machine

Last Updated on August 1, 2021 by Editorial Team

Author(s): Bassem Essam

Mathematics

Machine learning algorithms can be used as black boxes, but this is the worst way to use them. It’s crucial to understand how they work. The main points to understand any machine learning model is, how the model fits the data, what are the hyperparameters used in the model and how the model predicts the test data?
In this blog, we will try to understand the “Support Vector Machine” algorithm and the mathematics that the algorithm was built on it.

What is a Support Vector Machine?
Support Vector Machine is a supervised classification ML algorithm that is used to classify data points into two classes by finding the distance between data points groups and maximizing the gap between them.

A supervised ML algorithm means that the data set used to train the model is already labeled and the main task of the model is to classify the data points, unlike the unsupervised algorithms, which are based on unlabeled data sets, and find the categories of the classification with the relations between features.

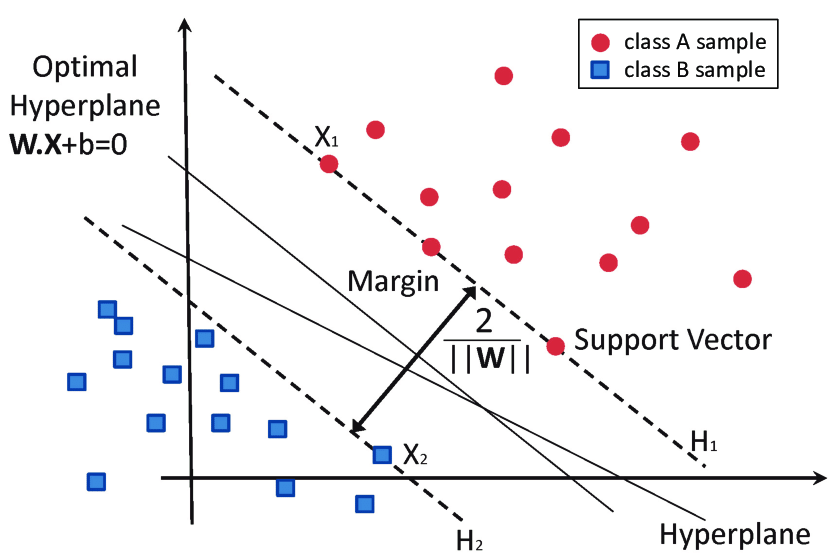
Let’s assume that we have the data points as shown in the diagram below. For simplicity, we will assume that we have only two independent variables.
A hyper-plan is a plane in space that is used to separate the two data points classes. The main task of the SVM model is to find the best hyper-plan to classify data points.

The hyper-plan can be expressed by the following equation.

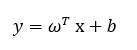
W is a vector of constants that represent the slopes of the plan. In this example, the vector can be represented with two constants [-1 and 0]. Now, let’s take two data points, one from each class, and find the projection of them to the hyper-plan. Assuming that the hyper-plan is passing through origin so, b = 0.
For the first data point (x1 = 4, x2 = 4), after substituting it to the hyper-plan equation, we find that the value of y is negative.

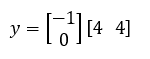
y = -1 * 4 + 0* 4 = -4 → negative

For the second data point (x1 = -4, x2 = -4), the value of y will be positive.

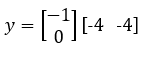
y = -1 * -4 + 0* -4 = 4 → positive
We see that the projection of any data point at one side of the hyper-plan is always positive and at the other side is always negative. At this point, we are able to classify the data points by projecting them to the hyper-plan and find the class of each point.

Now, we need to find the equation of the hyper-plan and the margin at the two sides of the hyper-plan in order to classify the data points. Also, we need to find the optimization function used to find the best vector for hyper-plan.
To find the margin lines, we will assume that the margin lines are passing through the nearest points in each class. so, the equations of the margin lines (or plans) are as follows.

To find the distance between two margin lines, we subtract the two data points, and hence, we find the following equation.

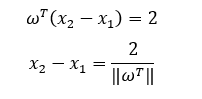
From the equation shown above, we need to maximize this function in order to find the best margin plans which guarantee that no data points are misclassified (this means that the minimum number of data points should be located in the margin areas and no data points are located in the other class).
The model should find the values of w and b that maximize the following function.

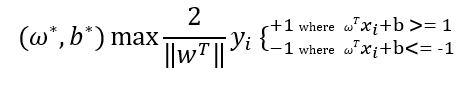
It can be expressed in a simpler way as below.

It can be expressed as minimize function as below.

Note that, the term of error summation has been added to the optimization function to overcome the over-fitting problem.

In real-life data sets, the data points cannot be classified using simple hyper-plans, but more complex classifiers are used. The kernel trick and soft margin technique are used to determine the equation of the classifier and the threshold.

In this blog, we discussed the simple concepts of SVM and the mathematics behind it. In the following blogs, we will dive deeper into more advanced techniques such as polynomial kernel and kernel tricks.

Thank you for reading!
Please contact me for any feedback or questions through my linked-in profile.

https://www.linkedin.com/in/bassemessam/

References:

https://www.researchgate.net/figure/Classification-of-data-by-support-vector-machine-SVM_fig8_304611323

https://www.youtube.com/watch?v=H9yACitf-KM&list=PLZoTAELRMXVPBTrWtJkn3wWQxZkmTXGwe&index=83

https://www.youtube.com/watch?v=efR1C6CvhmE

Mathematics Behind Support Vector Machine was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI