
Introduction To Linear Regression
Last Updated on July 24, 2023 by Editorial Team
Author(s): Manish Nayak
Originally published on Towards AI.
Introduction
One of the simplest models of machine learning is linear regression, but linear models are building blocks of deep neural networks and they are really important. There are two main classes of supervised learning problems, Regression and Classification. In regression, the value of the target is a real value, for example, we try to predict the salary of the given job description.
In classification, the value of the target is a finite set of classes for example if we’re given movie’s review and we try to predict the rating of a movie on a scale of one to five. In this post, I will try to explain linear regression.
Linear regression
Let’s give some definitions that will be very useful to understand. Consider an image, we try to analyze in machine learning is called an example. We denote this example by x, We describe each example with some characteristics and call it features. We denote these features by (x₁,x₂,x₃,…x????). In the case of an image, features are the intensities of every pixel. In supervised learning, we have target values, it means we have an answer for each example. We denote these target values by y. So for each example, xᵢ. The target value is yᵢ.

A set of examples and label pairs denoted by X large where the total number of pairs is L. Each pair have an example with its feature description, and target value. Finally, we want to find a modal, a function that maps examples to target values. We denoted this function by a(x) also known as model or hypothesis and the goal of machine learning is to find a modal that fits the training dataset in the best way.
Dataset Distribution
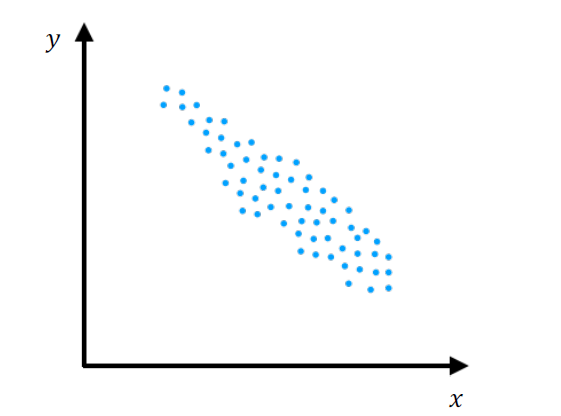
The above image showing the distribution of our dataset, we can see that there is a linear trend. If the feature increases two times, then the target decreases somewhere about two times. We can use some linear models to describe this data, to build a predictive model.
Linear Model

In the above image, the dark slanted line is the linear model. It is very simple and it has just two parameters, w₁, and w₀. If we find the best weights, w₁, and w₀, then we’ll have a model like this one. It describes data very well. It doesn’t predict the exact target value for each example, but it fits the data quite well. In most machine learning tasks, there are many features so, we can use a generic linear model like this one.

It takes each feature, xⱼ and multiplies it by weight wⱼ and sums this multiplication of all the features and then adds a biased term b. This is a linear model. It has d+1 parameters where d is the number of features in our dataset. There are d weights or coefficients and one bias term b.
Vector Notation
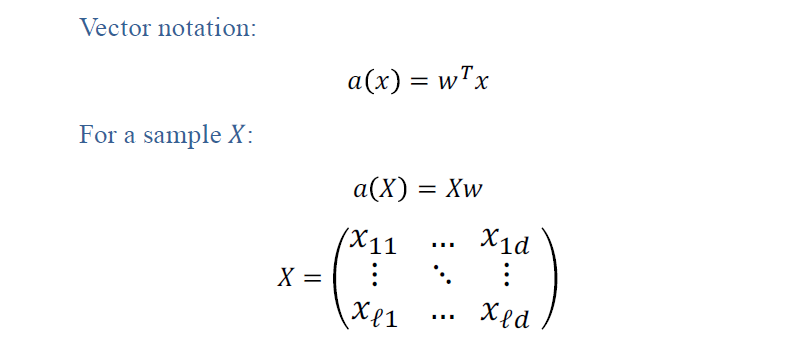
It is very convenient to write our linear model in vector form. It’s known from linear algebra that the above multiplication is dot product of transpose of weight vector and feature vector. It is a multiplication of vectors and then sums it up. So, our linear model is basically a dot product of weight vector W and feature vector X.
If we want to apply our model to a whole training dataset. For that, we form a matrix X with our sample. Matrix X is large and it has L rows and d columns. Each row corresponds to one example and each column corresponds to values of one feature on every example. We multiply matrix X by vector w and that is our predictions. This multiplication will give us a vector of size L and each component is a prediction of our linear model of each example.
Loss Function

The next question in machine learning is how to measure the accuracy or measure an error of a model on some dataset, or training dataset, or maybe test dataset. One of the most popular choices for loss function in regression is the mean squared error.
Mean Squared Error
It works like this. We take a particular example xᵢ and then calculate a prediction of our model on this example after that we subtract target value. We calculate the deviation of target value from predictive value, then we take a square of it and then we average these squares of deviations over all our training set. This is known as the mean squared error. It measures how well our model fits the data. The less mean squared error, the better the model fits the data. And of course, we can write mean squared error in vector form. We multiply matrix X by vector w and we have a vector of predictions for all the examples in the set, then we subtract vector of target values of real answers and then we take the euclidean norm of this vector. That is the same as the mean squared error I described before. So we have a loss function that measures how well our model fits on the data, then all we have to do is to minimize it with respect to w witch is parameters of our model.
Model Training

We want to find the parameters set w that give us minimum value of mean squared error on our training dataset. This is the essence of machine learning. We optimize loss to find the best model. Actually, if you know some calculus, then you can take derivatives and solve the equations.

There is also an analytical solution for these optimization problems. We can also find weight vector by using linear algebra method as shown in the above image but it involves the inverse of a matrix. It is a very costly operation if we have more than 100 or 1,000 features. We can reduce this problem to solve it as a system of linear equations, but it’s still quite hard and requires lots of computational resources. Later in another post, I will try to explain a framework for better and more scalable optimization of such problems.
Conclusion
In this post, I discussed linear models for regression. They are very simple, but they are very useful for deep neural networks. I also discussed mean squared error, a loss function for regression problems and we found out that it has an analytical solution, but it is not very good and hard to compute. In the upcoming post, we will try to find a better way to optimize such models.
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI
Take our 90+ lesson From Beginner to Advanced LLM Developer Certification: From choosing a project to deploying a working product this is the most comprehensive and practical LLM course out there!
Towards AI has published Building LLMs for Production—our 470+ page guide to mastering LLMs with practical projects and expert insights!

Discover Your Dream AI Career at Towards AI Jobs
Towards AI has built a jobs board tailored specifically to Machine Learning and Data Science Jobs and Skills. Our software searches for live AI jobs each hour, labels and categorises them and makes them easily searchable. Explore over 40,000 live jobs today with Towards AI Jobs!
Note: Content contains the views of the contributing authors and not Towards AI.














