Here Is Why You Probably Use numpy.std Incorrectly

Author(s): Leon Eversberg

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

How to estimate the standard deviation correctly in Python

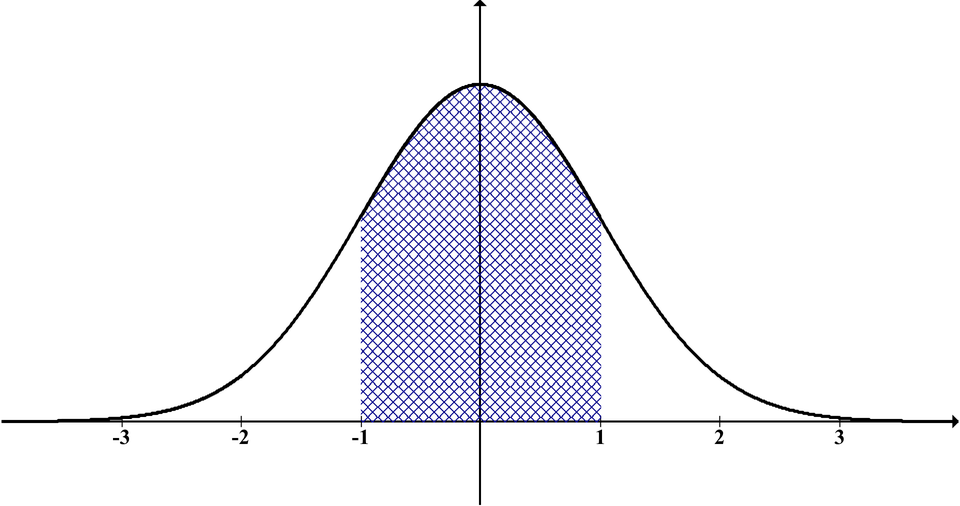
A normally distributed population with size N can be described with its mean μ and its standard deviation σ. This distribution is also known as a bell curve.

The standard deviation (std) can be computed using Eq. 1.

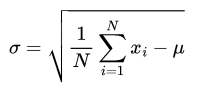
However, if we compute the standard deviation in Python with NumPy and pandas, we get different results.

In this article, you will learn the reason why this is the case.

np.std vs pandas std

Here is the output of NumPy’s std and the output of pandas std for some random data points X.

import numpy as np
import pandas as pd

X = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

df = pd.DataFrame({'X': X})

print(f"numpy std(X): {np.std(X)}")
>> numpy std(X): 2.8722813232690143

print(f"pandas std(df): {df.std()}")
>> pandas std(df): X    3.02765

As you can see, NumPy gives us a standard deviation of 2.87 and pandas gives us a standard deviation of 3.02. So, which one is true?

Bessel’s Correction

To understand the problem, we have to dive deeper into the topic of the standard deviation.

As Engineers or Scientists, we usually do not know the true population mean μ. However, we can calculate the sample mean from our data points x with the well-known Eq. 2.

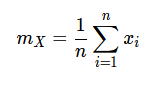
By replacing the population mean μ with the sample mean m, and the population size N with the sample size n in Eq. 1, we get the sample standard deviation s according to Eq. 3.

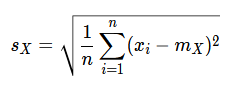
Given enough data points, we want the sample standard deviation s to be as close as possible to the true standard deviation of the population σ. Mathematically, this can be expressed using the expected value.

It turns out that this is not true for the sample standard deviation. Eq. 4 shows that the sample standard deviation is biased because of the additional term (n — 1)/n. For the full proof, see reference [1].

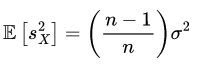
However, this can be corrected by replacing the n in Eq. 3 with (n — 1).

This is called Bessel’s correction, leading us to the unbiased estimator of Eq. 5.

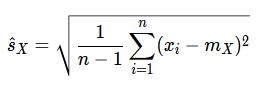
Explaining np.std vs pandas std

Given this knowledge, we can now explain the difference between np.std and pandas std functions.

By default, NumPy uses 1/n(Eq. 3), whereas pandas uses Bessel’s correction with 1/(n-1)(Eq. 4). We can change NumPy’s calculation by specifying the parameter ddof.

ddof: int, optional

Means Delta Degrees of Freedom. The divisor used in calculations is N – ddof, where N represents the number of elements. By default ddof is zero.

Going back to our initial Python example, we can now use the parameter ddof in np.std to get an unbiased estimate of the standard deviation.

import numpy as np
import pandas as pd

X = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

df = pd.DataFrame({'X': X})

print(f"pandas std(df): {df.std()}")
>> pandas std(df): X    3.02765

print(f"numpy std (X, ddof=1): {np.std(X, ddof=1)}")
>> numpy std (X, ddof=1): 3.0276503540974917

Setting the parameter ddof = 1 in np.std now gives us a standard deviation of 3.02. We get the same result with pandas.

Conclusion

Bessel’s correction fixes the bias from the sample standard deviation s by replacing n with n — 1.

NumPy’s std function uses the formula n — ddof. By default, NumPy uses ddof = 0 and pandas uses ddof = 1.

To sum it up, if you have some data points from a population and you want to estimate the unbiased standard deviation with NumPy, use np.std(X, ddof = 1).

References

[1] The Department of Mathematics and Computer Science, Bessel’s Correction (accessed: 14.12.2022)

M. Holický, Introduction to Probability and Statistics for Engineers (2013), Springer, Berlin, Heidelberg.

pandas.DataFrame.std: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.std.html (accessed: 14.12.2022)

numpy.std: https://numpy.org/doc/stable/reference/generated/numpy.std.html (accessed: 14.12.2022)

---

Here Is Why You Probably Use numpy.std Incorrectly was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI