Freezing Layers of a Deep Learning Model — the proper way

Author(s): Alexey Kravets

Originally published on Towards AI.

ADAM optimizer example in PyTorch

Introduction

It is often useful to freeze some of the parameters for example when you are fine-tuning your model and want to freeze some layers depending on the example you process like illustrated

As we can see for the first example we are freezing the first two layers, and updating the parameters of the last two while for the second example we freeze the second and forth layer and fine-tuning the others. There will be many other cases when this technique is useful and if are are reading this article you will probably have a case for this.

Problem setting

To simplify things a little bit, let’s assume we have a model that accepts two different types of inputs — one with 3 features an other with 2 features, and depending on which inputs are passed we are going to pass them through two different initial layers. Thus, we want to update only the parameters related to those particular inputs during training. As we can see below, we want to freeze hidden_task1 layer when input1 is passed and freeze hidden_task2 layer when input2 is passed.

class Network(nn.Module):
 def __init__(self):
 super().__init__()
 
 # Inputs to hidden layer linear transformation
 self.hidden_task1 = nn.Linear(3, 3, bias=False)
 self.hidden_task2 = nn.Linear(2, 3, bias=False)
 self.output = nn.Linear(3, 4, bias=False)
 
 # Define sigmoid activation and softmax output 
 self.sigmoid = nn.Sigmoid()
 self.softmax = nn.Softmax(dim=1)
 
 def forward(self, x, task='task1'):
 if task == 'task1': 
 x = self.hidden_task1(x)
 else:
 x = self.hidden_task2(x)
 x = self.sigmoid(x)
 x = self.output(x)
 x = self.softmax(x)

 return x
 
 def freeze_params(self, params_str):
 for n, p in self.named_parameters():
 if n in params_str:
 p.grad = None
 
 def freeze_params_grad(self, params_str):
 for n, p in self.named_parameters():
 if n in params_str:
 p.requires_grad = False
 
 def unfreeze_params_grad(self, params_str):
 for n, p in self.named_parameters():
 if n in params_str:
 p.requires_grad = True

# define input and target 
input1 = torch.randn(10, 3).to(device)
input2 = torch.randn(10, 2).to(device)

target1 = torch.randint(0, 4, (10, )).long().to(device) 
target2 = torch.randint(0, 4, (10, )).long().to(device) 

net = Network().to(device)

# helper 
def changed_parameters(initial, final):
 for n, p in initial.items():
 if not torch.allclose(p, final[n]):
 print("Changed : ", n)

In a world with only SGD optimizers

If we were working with SGD optimizer only, the problem would be solved simply using requires_grad = False that would not compute the gradients for the parameters we specify and thus we would obtain the desired results.

original_param = {n : p.clone() for (n, p) in net.named_parameters()}
print("Original params ")
pprint(original_param)
print(100 * "=")

# let's define 2 loss functions (we could only define one actually 
# in this case as they are the same) 
criterion1 = nn.CrossEntropyLoss()
criterion2 = nn.CrossEntropyLoss()

optimizer = optim.SGD(net.parameters(), lr=0.9)

# set requires_grad to False for selected layers
net.freeze_params_grad(['hidden_task2.weight'])

print("Params after task 1 update ")
params_hid1 = {n : p.clone() for (n, p) in net.named_parameters()}
pprint(params_hid1)
print(100 * "=")

# output for task 1 - we want to keep frozen task2 layer parameters
output = net(input1, task='task1')
optimizer.zero_grad() # zero the gradient buffers
loss1 = criterion(output, target)
loss1.backward()

optimizer.step()
print("States optimizer 1: ")
print(optimizer.state)
# set requires_grad back to True for selected layers
net.unfreeze_params_grad(['hidden_task2.weight'])

# output for task 2 - we want to keep frozen task1 layer parameters
output1 = net(input2, task='task2')
optimizer.zero_grad() # zero the gradient buffers
loss2 = criterion1(output1, target1)
loss2.backward()

optimizer.step() # Does the update

print("States optimizer 1: ")
print(optimizer.state)

# set requires_grad back to True for selected layers
net.unfreeze_params_grad(['hidden_task1.weight'])

print("Params after task 2 update ")
params_hid2 = {n : p.clone() for (n, p) in net.named_parameters()}
pprint(params_hid2)
changed_parameters(params_hid1, params_hid2)

In the outputs below we can see that the “Changed” parameter after the task 1 & task 2 updates are correct and we achieved the desired result.

{'hidden_task1.weight': tensor([[-0.0043, 0.3097, -0.4752],
 [-0.4249, -0.2224, 0.1548],
 [-0.0114, 0.4578, -0.0512]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1871, -0.2137],
 [-0.1390, -0.6755],
 [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.0214, 0.2282, 0.3464],
 [-0.3914, -0.2514, 0.2097],
 [ 0.4794, -0.1188, 0.4320],
 [-0.0931, 0.0611, 0.5228]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
====================================================================================================
Params after hidden 
{'hidden_task1.weight': tensor([[ 0.0010, 0.3107, -0.4746],
 [-0.4289, -0.2261, 0.1547],
 [-0.0105, 0.4596, -0.0528]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1871, -0.2137],
 [-0.1390, -0.6755],
 [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.0554, 0.2788, 0.3800],
 [-0.4105, -0.2702, 0.1917],
 [ 0.4552, -0.1496, 0.4091],
 [-0.0838, 0.0601, 0.5301]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
====================================================================================================
Changed : hidden_task1.weight
Changed : output.weight
Params after hidden 1 
{'hidden_task1.weight': tensor([[ 0.0010, 0.3107, -0.4746],
 [-0.4289, -0.2261, 0.1547],
 [-0.0105, 0.4596, -0.0528]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1906, -0.2102],
 [-0.1412, -0.6783],
 [-0.4657, -0.2929]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.0386, 0.2673, 0.3726],
 [-0.3818, -0.2414, 0.2232],
 [ 0.4402, -0.1698, 0.3898],
 [-0.0807, 0.0631, 0.5254]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
Changed : hidden_task2.weight
Changed : output.weight

Complications with Adaptive Optimizers

Now let’s try to run the same again, but using Adam optimizer :

optimizer = optim.Adam(net.parameters(), lr=0.9)

In the “Changed” part we now see that after the second task update, hidden_task1.weight got changed as well, which is not what we want.

Original params 
{'hidden_task1.weight': tensor([[-0.0043, 0.3097, -0.4752],
 [-0.4249, -0.2224, 0.1548],
 [-0.0114, 0.4578, -0.0512]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1871, -0.2137],
 [-0.1390, -0.6755],
 [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.0214, 0.2282, 0.3464],
 [-0.3914, -0.2514, 0.2097],
 [ 0.4794, -0.1188, 0.4320],
 [-0.0931, 0.0611, 0.5228]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
====================================================================================================
Params after hidden 
{'hidden_task1.weight': tensor([[ 0.8957, 1.2069, 0.4291],
 [-1.3211, -1.1204, -0.7465],
 [ 0.8887, 1.3537, -0.9508]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1871, -0.2137],
 [-0.1390, -0.6755],
 [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.9212, 1.1262, 1.2433],
 [-1.2879, -1.1492, -0.6922],
 [-0.4249, -1.0177, -0.4718],
 [ 0.8078, -0.8394, 1.4181]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
====================================================================================================

Changed : hidden_task1.weight
Changed : output.weight

Params after hidden 1 
{'hidden_task1.weight': tensor([[ 1.4907, 1.7991, 1.0283],
 [-1.9122, -1.7133, -1.3428],
 [ 1.4837, 1.9445, -1.5453]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[-0.7146, -1.1118],
 [-1.0377, 0.2305],
 [-1.3641, -1.1889]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.9372, 1.3922, 1.5032],
 [-1.5886, -1.4844, -0.9789],
 [-0.8855, -1.5812, -1.0326],
 [ 1.6785, -0.2048, 2.3004]], device='cuda:0',
 grad_fn=<CloneBackward0>)}


Changed : hidden_task1.weight
Changed : hidden_task2.weight
Changed : output.weight

Let’s try to understand what is going on here. The update rule for SGD is defined as:

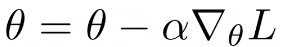
Where alpha is the learning rate, nabla L is the gradient with respect to the parameters. As we can see, if the gradient is zero the parameters do not get updated as the updates rule is only a function of the gradients. And when we set requires_grad = False the gradients will be zero for those layers and won’t be computed.

What about Adaptive optimizers such as ADAM or others where the update rule is not only a function of the gradients? Let’s look at ADAM:

Where Beta1, Beta2 are some hyper-parameters, alpha is the learning rate, mt is the first moment and vt is the second moment of the gradients gt. This update rule allows to compute adaptive learning rates for each parameter.
Most importantly for our problem, even if the current gradient gt is set to zero through requires_grad = False , the parameters are still updated by the optimizer using the stored mt and vt values. Indeed, if we print optimizer.state we can see that the optimizer stores the number of steps (i.e., the number of gradient updates that each parameter had), exp_avg, which is the first moment and exp_avg_sq the second moment:

# optimizer step 1
defaultdict(<class 'dict'>, {Parameter containing:
tensor([[ 0.8957, 1.2069, 0.4291],
 [-1.3211, -1.1204, -0.7465],
 [ 0.8887, 1.3537, -0.9508]], device='cuda:0', requires_grad=True):
 {'step': tensor(1.), 
'exp_avg': tensor([[-5.9304e-04, -1.0966e-04, -5.9985e-05],
 [ 4.4068e-04, 4.1636e-04, 1.7705e-05],
 [-1.0544e-04, -2.0357e-04, 1.7783e-04]], device='cuda:0'), 
'exp_avg_sq': tensor([[3.5170e-08, 1.2025e-09, 3.5982e-10],
 [1.9420e-08, 1.7336e-08, 3.1345e-11],
 [1.1118e-09, 4.1440e-09, 3.1623e-09]], device='cuda:0')}, 
Parameter containing:
tensor([[ 0.9212, 1.1262, 1.2433],
 [-1.2879, -1.1492, -0.6922],
 [-0.4249, -1.0177, -0.4718],
 [ 0.8078, -0.8394, 1.4181]], device='cuda:0', requires_grad=True):
 {'step': tensor(1.), 
'exp_avg': tensor([[-0.0038, -0.0056, -0.0037],
 [ 0.0021, 0.0021, 0.0020],
 [ 0.0027, 0.0034, 0.0025],
 [-0.0010, 0.0001, -0.0008]], device='cuda:0'), 
'exp_avg_sq': tensor([[1.4261e-06, 3.1517e-06, 1.3953e-06],
 [4.4782e-07, 4.3352e-07, 3.9994e-07],
 [7.2213e-07, 1.1702e-06, 6.4754e-07],
 [1.0547e-07, 1.2353e-09, 6.5470e-08]], device='cuda:0')}})

# optimizer step 2
tensor([[ 1.4907, 1.7991, 1.0283],
 [-1.9122, -1.7133, -1.3428],
 [ 1.4837, 1.9445, -1.5453]], device='cuda:0', requires_grad=True): 
{'step': tensor(2.), 
'exp_avg': tensor([[-5.3374e-04, -9.8693e-05, -5.3987e-05],
 [ 3.9661e-04, 3.7472e-04, 1.5934e-05],
 [-9.4899e-05, -1.8321e-04, 1.6005e-04]], device='cuda:0'), 
'exp_avg_sq': tensor([[3.5135e-08, 1.2013e-09, 3.5946e-10],
 [1.9400e-08, 1.7318e-08, 3.1314e-11],
 [1.1107e-09, 4.1398e-09, 3.1592e-09]], device='cuda:0')}, 
Parameter containing:
tensor([[ 0.9372, 1.3922, 1.5032],
 [-1.5886, -1.4844, -0.9789],
 [-0.8855, -1.5812, -1.0326],
 [ 1.6785, -0.2048, 2.3004]], device='cuda:0', requires_grad=True): 
{'step': tensor(2.), 'exp_avg': tensor([[-0.0002, -0.0025, -0.0017],
 [ 0.0011, 0.0011, 0.0010],
 [ 0.0019, 0.0029, 0.0021],
 [-0.0028, -0.0015, -0.0014]], device='cuda:0'), 
'exp_avg_sq': tensor([[2.4608e-06, 3.7819e-06, 1.6833e-06],
 [5.1839e-07, 4.8712e-07, 4.7173e-07],
 [7.4856e-07, 1.1713e-06, 6.4888e-07],
 [4.4950e-07, 2.6660e-07, 1.1588e-07]], device='cuda:0')}, 
Parameter containing:
tensor([[-0.7146, -1.1118],
 [-1.0377, 0.2305],
 [-1.3641, -1.1889]], device='cuda:0', requires_grad=True): 
{'step': tensor(1.), 
'exp_avg': tensor([[ 0.0009, 0.0011],
 [ 0.0045, -0.0002],
 [ 0.0003, 0.0012]], device='cuda:0'), 
'exp_avg_sq': tensor([[8.7413e-08, 1.3188e-07],
 [1.9946e-06, 4.3840e-09],
 [8.1403e-09, 1.3691e-07]], device='cuda:0')}})

We can see that in the first optimizer.step() update we get only two parameters in the optimizer states — hidden_task1and output . In the second optimizer’s step, we have all the parameters but notice that hidden_task1 is updated twice which it shouldn’t.

So how to deal with them? The solution is actually very simple — instead of using requires_grad set simply set grad = None for the parameters. The code thus becomes:

original_param = {n : p.clone() for (n, p) in net.named_parameters()}
print("Original params ")
pprint(original_param)
print(100 * "=")

# let's define 2 loss functions (we could only define one actually 
# in this case as they are the same) 
criterion1 = nn.CrossEntropyLoss()
criterion2 = nn.CrossEntropyLoss()

optimizer = optim.SGD(net.parameters(), lr=0.9)


print("Params after task 1 update ")
params_hid1 = {n : p.clone() for (n, p) in net.named_parameters()}
pprint(params_hid1)
print(100 * "=")

# output for task 1 - we want to keep frozen task2 layer parameters
output = net(input1, task='task1')
optimizer.zero_grad() # zero the gradient buffers
loss1 = criterion1(output, target1)
loss1.backward()
# Freeze parameters here!
net.freeze_params(['hidden_task2.weight'])
optimizer.step()

# output for task 2 - we want to keep frozen task1 layer parameters
output = net(input2, task='task2')
optimizer.zero_grad() # zero the gradient buffers
loss2 = criterion2(output, target2)
loss2.backward()
# Freeze parameters here!
net.freeze_params_grad(['hidden_task1.weight'])
optimizer.step() # Does the update

print("Params after task 2 update ")
params_hid2 = {n : p.clone() for (n, p) in net.named_parameters()}
pprint(params_hid2)
changed_parameters(params_hid1, params_hid2)

Note that we need to set grad = None after loss.backward() as we need to compute the gradients for all the parameters first, but before optimizer.step().

If we run the code now the ADAM optimizer, the results are as expected

Original params 
{'hidden_task1.weight': tensor([[-0.0043, 0.3097, -0.4752],
 [-0.4249, -0.2224, 0.1548],
 [-0.0114, 0.4578, -0.0512]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1871, -0.2137],
 [-0.1390, -0.6755],
 [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.0214, 0.2282, 0.3464],
 [-0.3914, -0.2514, 0.2097],
 [ 0.4794, -0.1188, 0.4320],
 [-0.0931, 0.0611, 0.5228]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
====================================================================================================
Params after task 1 update 
{'hidden_task1.weight': tensor([[ 0.8957, 1.2069, 0.4291],
 [-1.3211, -1.1204, -0.7465],
 [ 0.8887, 1.3537, -0.9508]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[ 0.1871, -0.2137],
 [-0.1390, -0.6755],
 [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.9212, 1.1262, 1.2433],
 [-1.2879, -1.1492, -0.6922],
 [-0.4249, -1.0177, -0.4718],
 [ 0.8078, -0.8394, 1.4181]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
====================================================================================================
Changed : hidden_task1.weight
Changed : output.weight
Params after task 2 update 
{'hidden_task1.weight': tensor([[ 0.8957, 1.2069, 0.4291],
 [-1.3211, -1.1204, -0.7465],
 [ 0.8887, 1.3537, -0.9508]], device='cuda:0',
 grad_fn=<CloneBackward0>),
 'hidden_task2.weight': tensor([[-0.7146, -1.1118],
 [-1.0377, 0.2305],
 [-1.3641, -1.1889]], device='cuda:0', grad_fn=<CloneBackward0>),
 'output.weight': tensor([[ 0.9372, 1.3922, 1.5032],
 [-1.5886, -1.4844, -0.9789],
 [-0.8855, -1.5812, -1.0326],
 [ 1.6785, -0.2048, 2.3004]], device='cuda:0',
 grad_fn=<CloneBackward0>)}
Changed : hidden_task2.weight
Changed : output.weight

Also the optimizer.state is now different — in the second optimizer’s step hidden_task1 is not updated and its step value is 1.

tensor([[ 0.8957, 1.2069, 0.4291],
 [-1.3211, -1.1204, -0.7465],
 [ 0.8887, 1.3537, -0.9508]], device='cuda:0', requires_grad=True): 
{'step': tensor(1.), 
'exp_avg': tensor([[-5.9304e-04, -1.0966e-04, -5.9985e-05],
 [ 4.4068e-04, 4.1636e-04, 1.7705e-05],
 [-1.0544e-04, -2.0357e-04, 1.7783e-04]], device='cuda:0'), 
'exp_avg_sq': tensor([[3.5170e-08, 1.2025e-09, 3.5982e-10],
 [1.9420e-08, 1.7336e-08, 3.1345e-11],
 [1.1118e-09, 4.1440e-09, 3.1623e-09]], device='cuda:0')}, 
Parameter containing:
tensor([[ 0.9372, 1.3922, 1.5032],
 [-1.5886, -1.4844, -0.9789],
 [-0.8855, -1.5812, -1.0326],
 [ 1.6785, -0.2048, 2.3004]], device='cuda:0', requires_grad=True): 
{'step': tensor(2.), 
'exp_avg': tensor([[-0.0002, -0.0025, -0.0017],
 [ 0.0011, 0.0011, 0.0010],
 [ 0.0019, 0.0029, 0.0021],
 [-0.0028, -0.0015, -0.0014]], device='cuda:0'), 
'exp_avg_sq': tensor([[2.4608e-06, 3.7819e-06, 1.6833e-06],
 [5.1839e-07, 4.8712e-07, 4.7173e-07],
 [7.4856e-07, 1.1713e-06, 6.4888e-07],
 [4.4950e-07, 2.6660e-07, 1.1588e-07]], device='cuda:0')}, 
Parameter containing:
tensor([[-0.7146, -1.1118],
 [-1.0377, 0.2305],
 [-1.3641, -1.1889]], device='cuda:0', requires_grad=True): 
{'step': tensor(1.), 
'exp_avg': tensor([[ 0.0009, 0.0011],
 [ 0.0045, -0.0002],
 [ 0.0003, 0.0012]], device='cuda:0'), 
'exp_avg_sq': tensor([[8.7413e-08, 1.3188e-07],
 [1.9946e-06, 4.3840e-09],
 [8.1403e-09, 1.3691e-07]], device='cuda:0')}})

Distributed Data Parallel

As an additional note, in case we want the support of DistributedDataParallel in PyTorch to work with multiple GPUs, we need to slightly modify the implementation described above as follows:

It is a little bit more complicated, and if you know of a cleaner way to write it please share in the comments!

Feedback

I would appreciate any feedback on the above — if you know whether there might be any potential problems doing it this way and if there are other ways to achieve the same.

Conclusions

In this article, we described how to do layers freezing when during training we need to freeze and unfreeze some layers. If what you want is to freeze completely some of the layers during the whole training, you can use both solutions described in this article, as it would not matter in your case whether you are using SGD or an adaptive optimizer. However, as we have seen, the issue arises when you need to freeze and unfreeze layers during training, and the different behavior we see when using optimizers whose update rule only depends on the gradient and the ones whose update rule depends on other variables such as momentum. You can also find the full code here.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI