And Data Asks, “Do I Look Normal to You?”

Author(s): Sanket Shinde

Originally published on Towards AI.

Data Science

Normality tests for data science

It is very important as a data analyst or data scientist, one has to assess a sample data at first, source of sample data can be primary or secondary but it is very important to analyze the nature of the data.

Let’s put this into a hypothesis as follows,

NULL Hypothesis: On average, sample data distribution is normal

ALTERNATE Hypothesis: On average, sample data distribution is not normal

What does it mean? Hypothesis Formulations

Let us see, here we have put the null hypothesis as data is normally distributed, typically it depicts that if data is normal then we will not take any action and we will proceed for building a prediction model.

In case of alternate hypothesis, it depicts that if data is not normally distributed then we will have to take any action before proceeding for building a prediction model, typical action as a data scientist can be the normalization of a data once this corrective action is taken then only he or she will proceed for building a prediction model.

Strategies to test normality of data

Now in order to test whether a sample data is normal or not, we will decide strategies at first that are as follows,

Data Visualization Methods:

These will visualize the nature of data but not able to quantify the same.

1. Plotting a histogram, graphical distribution of frequencies within the range
2. Plotting Q-Q plot, a graphical method for comparing of probability distributions.

Statistical Tests/Methods:

1. Calculating p-value based on D’Agostino’s K² Normality Test
2. Calculating p-value based on Shapiro-Wilk’s(S-W) Normality Test

Our Assumptions

Please note that we have considered the following values,

The level of confidence as 95%, which means we are 95% confident that our decision will not go wrong.
The level of significance as 5%, which means there is a 5% chance that our decision will go wrong.

It is an industry-standard/norm that the level of confidence is assumed as 95%,
It means a 5% error is permissible.

Conduct an experiment to test a hypothesis

Strategy 1: Plotting a Histogram

The most common visualization tool to analyze the distribution of data is a histogram. In which, the data is divided into the predefined set of bins. on the Y-axis of a plot, we always have frequency or occurrence of values within a bin.
These bins are placed in ascending order on the X-axis of a plot.

To check the normality of a sample data distribution, one can subjectively infer based on histograms that whether sample data has followed a normal distribution or not(in other words, whether data distribution follows a bell curve or not).

We have used the R programming environment [R-studio] for the implementation

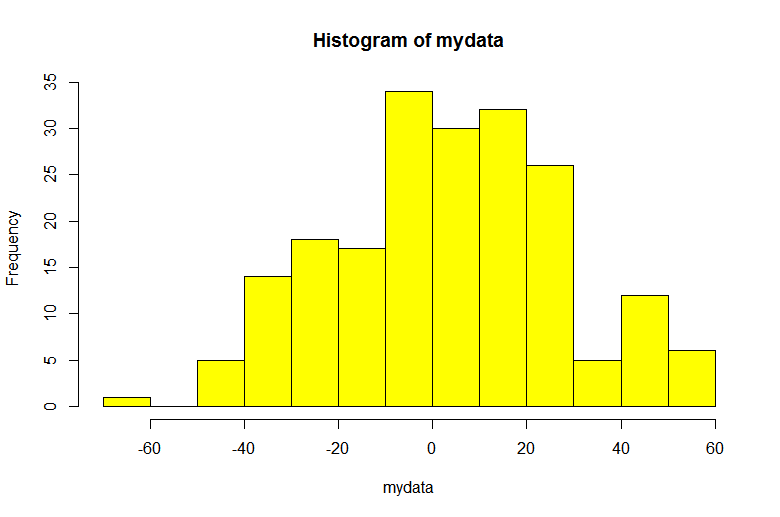
Based on the above histogram, one can infer that data is normally distributed across a range of values(bins) but one cant justifies quantitatively without the help of statistical methods.

Strategy 2: Plotting a Q-Q Plot

A Q-Q plot is typically a scatter plot that does allow us to compare quantiles of respective data distributions(x vs. y). We will use a variant of the Q-Q plot that is a Normal Q-Q plot which does compare quantiles of standard normal distribution(x-axis) with sample data distribution(y-axis). If a plot gives a fairly straight line then we can subjectively confirm that sample data is derived from a normally distributed population i.e. its normally distributed data.

We have used the R programming environment [R-studio] for the implementation

In the above q-q plot, we can easily find out the plotted points are scattered approximately across the straight line which confirms that data strongly follow a normal distribution but again our claim cant be justified quantitatively.

Strategy 3: D’Agostino’s K² Normality Test

This statistical test allows us to find a significant skewness component in a data distribution. Skewness is a measure of asymmetricity in a data distribution.

This test mainly gives two values,

statistic: s²+k², where s is the z-score returned by skewtest and k is the z-score returned by kurtosistest.

p value: It ranges between 0 and 1, it is a calculated probability of a given statistical model when null hypothesis is true.

Important Consideration

One should note the following rule for acceptance/rejection of the null hypothesis,

If p is high, NULL will FLY (Accept NULL Hypothesis / Data failed to reject the NULL Hypothesis)

If p is low, NULL will GO (Reject NULL Hypothesis / Accept ALTERNATE Hypothesis)

Here ‘p’ means the p-value obtained from the statistical test.

import numpy as npimport scipy.stats as sc#generate random seednp.random.seed(1)#generate random set of numbersvalue=15+7*np.random.randn(50)print("Size of univariate observations-:",len(value))statval,pval=sc.normaltest(value)print("Statistics: ",statval)print("P-value: ",pval)alpha=0.05if(pval>alpha): print("Null Hypothesis: Data Distribution is Normal, Wins!!!")else: print("Alt Hypothesis: Data Distribution is not Normal, Wins!!!")

Output for the above code snippet is:

Size of univariate observations-: 50
Statistics: 0.44153052875099047
P-value: 0.801904893845168
Null Hypothesis: Data Distribution is Normal, Wins!!!

Strategy 4: Shapiro-Wilk’s Normality Test

This test verifies a set of data values and tries to figure out if the dataset has a normal distribution or not.

In practice, the Shapiro-Wilk test is believed to be a reliable test of normality, although there is some suggestion that the test may be suitable for smaller samples of data, e.g. thousands of observations or fewer.

The Shapiro() SciPy function will calculate the Shapiro-Wilk on a given dataset. The function returns both the W-statistic calculated by the test and the p-value.

The complete example of performing the Shapiro-Wilk test on the dataset is listed below.

import numpy as npimport scipy.stats as sc#generate random seednp.random.seed(1)#generate random set of numbersvalue=15+7*np.random.randn(50)print("Size of univariate observations-:",len(value))statval,pval=sc.shapiro(value)print("Statistics: ",statval)print("P-value: ",pval)alpha=0.05if(pval>alpha):
 print("Null Hypothesis: Data Distribution is Normal, Wins!!!")else:
 print("Alt Hypothesis: Data Distribution is not Normal, Wins!!!")

Output for the above code snippet is:

Size of univariate observations-: 50
Statistics: 0.9704716205596924
P-value: 0.24187302589416504
Null Hypothesis: Data Distribution is Normal, Wins!!!

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI