Recommendation System Tutorial with Python using Collaborative Filtering
Last Updated on November 15, 2020 by Editorial Team
Building a recommendation system using Python and collaborative filtering for a Netflix use case.
Introduction
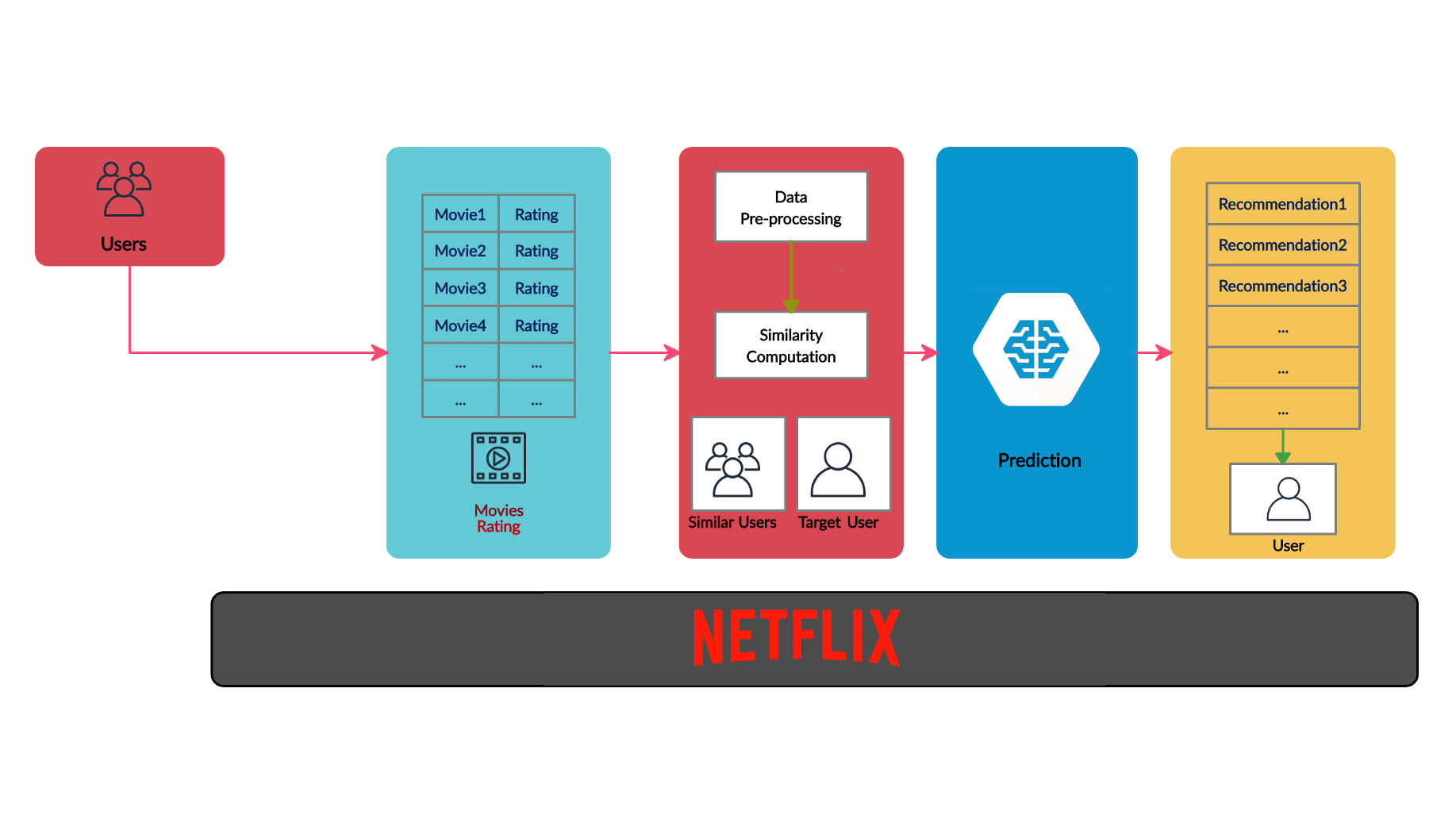
A recommendation system generates a compiled list of items in which a user might be interested, in the reciprocity of their current selection of item(s). It expands users’ suggestions without any disturbance or monotony, and it does not recommend items that the user already knows. Similarly, the Netflix recommendation system offers recommendations by matching and searching similar users’ habits and suggesting movies that share characteristics with films that users have rated highly.
This tutorial’s code is available on Github and its full implementation as well on Google Colab.

The recommendation system workflow shown in the diagram above shows the user’s collaboration regarding the ratings of different movies or shows. New users get their recommendations based on the recommendations of existing users.
According to McKinsey:
75% of what people are watching on Netflix comes from recommendations [1].
Netflix Real-time data cases:
- More than 20,000 movies and shows.
- 2 million users.
Complications
Recommender systems are machine learning-based systems that scan through all possible options and provides a prediction or recommendation. However, building a recommendation system has below complications:
- Users’ data is interchangeable.
- The data volume is large and includes a significant list of movies, shows, customers’ profiles and interests, ratings, and other data points.
- New registered customers use to have very limited information.
- Real-time prediction for users.
- Old users can have an overabundance of information.
- It should not show items that are very different or too similar.
- Users can change the rating of items on change of his/her mind.
Types of Recommendation Systems
There are two types of recommendation systems:
- Content filtering recommender systems.
- Collaborative filtering based recommender systems.
Fun fact: Netflix‘s recommender system filtering architecture bases on collaborative filtering [2] [3].
Content Filtering
Content filtering expects the side information such as the properties of a song (song name, singer name, movie name, language, and others.). Recommender systems perform well, even if new items are added to the library. A recommender system’s algorithm expects to include all side properties of its library’s items.
An essential aspect of content filtering:
- Expects item information.
- Item information should be in a text document.
Collaborative Filtering
The idea behind collaborative filtering is to consider users’ opinions on different videos and recommend the best video to each user based on the user’s previous rankings and the opinion of other similar types of users.

Pros:
- It does not need a movie’s side knowledge like genres.
- It uses information collected from other users to recommend new items to the current user.
Cons:
- It does not achieve recommendation on a new movie or shows that have no ratings.
- It requires the user community and can have a sparsity problem.
Different techniques of Collaborative filtering:
Non-probabilistic algorithm
- User-based nearest neighbor.
- Item-based nearest neighbor.
- Reducing dimensionality.
Probabilistic algorithm
- Bayesian-network model.
- EM algorithm.
Issues in Collaborative Filtering
There are several challenges for collaborative filtering, as mentioned below:
Sparseness
The Netflix recommendation system’s dataset is extensive, and the user-item matrix used for the algorithm could be vast and sparse, so this encounters the problem of performance.

The sparsity of data derives from the ratio of the empty and total records in the user-item matrix.
Sparsity = 1 — |R|/|I|*|U|
Where,
R = Rating
I = Items
U = Users
Cold Start
This problem encounters when the system has no information to make recommendations for the new users. As a result, the matrix factorization techniques cannot apply.
This problem brings two observations:
- How to recommend a new video for users?
- What video to recommend to new users?
Solutions:
- Suggest or ask users to rate videos.
- Default voting for videos.
- Use other techniques like content-based or demographic for the initial phase.
User-based Nearest Neighbor
The basic technique of user-based Nearest Neighbor for the user John:
John is an active Netflix user and has not seen a video “v” yet. Here, the user-based nearest neighbor algorithm will work like below:
- The technique finds a set of users or nearest neighbors who have liked the same items as John in the past and have rated video “v.”
- Algorithm predicts.
- Performs for all the items John has not seen and recommends.
Essentially, the user-based nearest neighbor algorithm generates a prediction for item i by analyzing the rating for i from users in u’s neighborhood.
Let’s calculate user similarity for the prediction:

Where:
a, b = Users
r(a, p)= Rating of user a for item p
P = Set of items. Rated by both users a and b

Prediction based on the similarity function:

Here, similar users are defined by those that like similar movies or videos.
Challenges
- For a considerable amount of data, the algorithm encounters severe performance and scaling issues.
- Computationally expansiveness O(MN) can encounter in the worst case. Where M is the number of customers and N is the number of items.
- Performance can be increase by applying the methodology of dimensionality reduction. However, it can reduce the quality of the recommendation system.
Item-based Nearest Neighbor
This technique generates predictions based on similarities between different videos or movies or items.
Prediction for a user u and item i is composed of a weighted sum of the user u’s ratings for items most similar to i.


As shown in figure 8, look for the videos that are similar to video5. Hence, the recommendation is very similar to video4.
Role of Cosine Similarity in building Recommenders
The cosine similarity is a metric used to find the similarity between the items/products irrespective of their size. We calculate the cosine of an angle by measuring between any two vectors in a multidimensional space. It is applicable for supporting documents of a considerable size due to the dimensions.
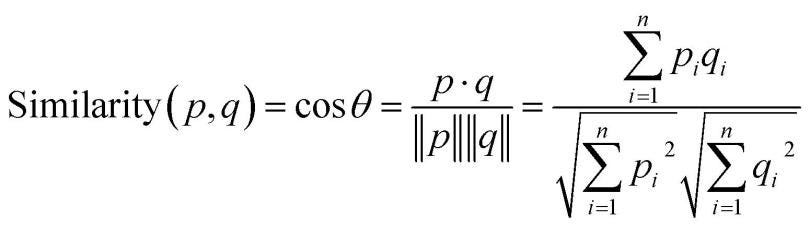
Where:
cosine is an angle calculated between -1 to 1 where -1 denotes dissimilar items, and 1 shows items which are a correct match.
cos p. q — gives the dot product between the vectors.
||p|| ||q|| — represents the product of vector’s magnitude
Why do Baseline Predictors for Recommenders matter?
Baseline Predictors are independent of the user’s rating, but they provide predictions to the new user’s
General Baseline form
bu,i = µ + bu + bi
Where,
bu and bi are users and item baseline predictors.
Motivation for Baseline
- Imputation of missing values with baseline values.
- compare accuracy with advanced model
Netflix Movie Recommendation System
Problem Statement
Netflix is a platform that provides online movie and video streaming. Netflix wants to build a recommendation system to predict a list of movies for users based on other movies’ likes or dislikes. This recommendation will be for every user based on his/her unique interest.
Netflix Dataset
- combine_data_2.txt: This text file contains movie_id, customer_id, rating, date
- movie_title.csv: This CSV file contains movie_id and movie_title
Load Dataset
from datetime import datetime import pandas as pd import numpy as np import seaborn as sns import os import random import matplotlib import matplotlib.pyplot as plt from scipy import sparse from sklearn.metrics.pairwise import cosine_similarity from sklearn.metrics import mean_squared_errorimport xgboost as xgb from surprise import Reader, Dataset from surprise import BaselineOnly from surprise import KNNBaseline from surprise import SVD from surprise import SVDpp from surprise.model_selection import GridSearchCVdef load_data(): netflix_csv_file = open("netflix_rating.csv", mode = "w") rating_files = ['combined_data_1.txt'] for file in rating_files: with open(file) as f: for line in f: line = line.strip() if line.endswith(":"): movie_id = line.replace(":", "") else: row_data = [] row_data = [item for item in line.split(",")] row_data.insert(0, movie_id) netflix_csv_file.write(",".join(row_data)) netflix_csv_file.write('\n') netflix_csv_file.close() df = pd.read_csv('netflix_rating.csv', sep=",", names = ["movie_id","customer_id", "rating", "date"]) return dfnetflix_rating_df = load_data() netflix_rating_df.head()

Analysis of Dataset
Find duplicate ratings:
netflix_rating_df.duplicated(["movie_id","customer_id", "rating", "date"]).sum()
Split train and test data:
split_value = int(len(netflix_rating_df) * 0.80) train_data = netflix_rating_df[:split_value] test_data = netflix_rating_df[split_value:]
Count number of ratings in the training data set:
plt.figure(figsize = (12, 8))
ax = sns.countplot(x="rating", data=train_data)ax.set_yticklabels([num for num in ax.get_yticks()])plt.tick_params(labelsize = 15)
plt.title("Count Ratings in train data", fontsize = 20)
plt.xlabel("Ratings", fontsize = 20)
plt.ylabel("Number of Ratings", fontsize = 20)
plt.show()

Find the number of rated movies per user:
no_rated_movies_per_user = train_data.groupby(by = "customer_id")["rating"].count().sort_values(ascending = False) no_rated_movies_per_user.head()

Find the Rating number per Movie:
no_ratings_per_movie = train_data.groupby(by = "movie_id")["rating"].count().sort_values(ascending = False) no_ratings_per_movie.head()

Create User-Item Sparse Matrix
In a user-item sparse matrix, items’ values are present in the column, and users’ values are present in the rows. The rating of the user is present in the cell. Such is a sparse matrix because there can be the possibility that the user cannot rate every movie items, and many items can be empty or zero.
def get_user_item_sparse_matrix(df):
sparse_data = sparse.csr_matrix((df.rating, (df.customer_id, df.movie_id)))
return sparse_data
User-item Train Sparse matrix
train_sparse_data = get_user_item_sparse_matrix(train_data)
User-item test sparse matrix
test_sparse_data = get_user_item_sparse_matrix(test_data)
Global Average Rating
global_average_rating = train_sparse_data.sum()/train_sparse_data.count_nonzero()
print("Global Average Rating: {}".format(global_average_rating))

Check the Cold Start Problem

Calculate the average rating
def get_average_rating(sparse_matrix, is_user):
ax = 1 if is_user else 0
sum_of_ratings = sparse_matrix.sum(axis = ax).A1
no_of_ratings = (sparse_matrix != 0).sum(axis = ax).A1
rows, cols = sparse_matrix.shape
average_ratings = {i: sum_of_ratings[i]/no_of_ratings[i] for i in range(rows if is_user else cols) if no_of_ratings[i] != 0}
return average_ratings
Average Rating User
average_rating_user = get_average_rating(train_sparse_data, True)
Average Rating Movie
avg_rating_movie = get_average_rating(train_sparse_data, False)
Check Cold Start Problem: User
total_users = len(np.unique(netflix_rating_df["customer_id"]))
train_users = len(average_rating_user)
uncommonUsers = total_users - train_users
print("Total no. of Users = {}".format(total_users))
print("No. of Users in train data= {}".format(train_users))
print("No. of Users not present in train data = {}({}%)".format(uncommonUsers, np.round((uncommonUsers/total_users)*100), 2))

Here, 1% of total users are new, and they will have no proper rating available. Therefore, this can bring the issue of the cold start problem.
Check Cold Start Problem: Movie
total_movies = len(np.unique(netflix_rating_df["movie_id"]))
train_movies = len(avg_rating_movie)
uncommonMovies = total_movies - train_movies
print("Total no. of Movies = {}".format(total_movies))
print("No. of Movies in train data= {}".format(train_movies))
print("No. of Movies not present in train data = {}({}%)".format(uncommonMovies, np.round((uncommonMovies/total_movies)*100), 2))

Here, 20% of total movies are new, and their rating might not be available in the dataset. Consequently, this can bring the issue of the cold start problem.
Similarity Matrix
A similarity matrix is critical to measure and calculate the similarity between user-profiles and movies to generate recommendations. Fundamentally, this kind of matrix calculates the similarity between two data points.

In the matrix shown in figure 17, video2 and video5 are very similar. The computation of the similarity matrix is a very tedious job because it requires a powerful computational system.
Compute User Similarity Matrix
Computation of user similarity to find similarities of the top 100 users:
def compute_user_similarity(sparse_matrix, limit=100):
row_index, col_index = sparse_matrix.nonzero()
rows = np.unique(row_index)
similar_arr = np.zeros(61700).reshape(617,100)
for row in rows[:limit]:
sim = cosine_similarity(sparse_matrix.getrow(row), train_sparse_data).ravel()
similar_indices = sim.argsort()[-limit:]
similar = sim[similar_indices]
similar_arr[row] = similar
return similar_arrsimilar_user_matrix = compute_user_similarity(train_sparse_data, 100)
Compute Movie Similarity Matrix
Load movies title data set
movie_titles_df = pd.read_csv("movie_titles.csv",sep = ",", header = None, names=['movie_id', 'year_of_release', 'movie_title'],index_col = "movie_id", encoding = "iso8859_2")movie_titles_df.head()

Compute similar movies:
def compute_movie_similarity_count(sparse_matrix, movie_titles_df, movie_id):
similarity = cosine_similarity(sparse_matrix.T, dense_output = False)
no_of_similar_movies = movie_titles_df.loc[movie_id][1], similarity[movie_id].count_nonzero()
return no_of_similar_movies
Get a similar movies list:
similar_movies = compute_movie_similarity_count(train_sparse_data, movie_titles_df, 1775)
print("Similar Movies = {}".format(similar_movies))

Building the Machine Learning Model
Create a Sample Sparse Matrix
def get_sample_sparse_matrix(sparseMatrix, n_users, n_movies):
users, movies, ratings = sparse.find(sparseMatrix)
uniq_users = np.unique(users)
uniq_movies = np.unique(movies)
np.random.seed(15)
userS = np.random.choice(uniq_users, n_users, replace = False)
movieS = np.random.choice(uniq_movies, n_movies, replace = False)
mask = np.logical_and(np.isin(users, userS), np.isin(movies, movieS))
sparse_sample = sparse.csr_matrix((ratings[mask], (users[mask], movies[mask])),
shape = (max(userS)+1, max(movieS)+1))
return sparse_sample
Sample Sparse Matrix for the training data:
train_sample_sparse_matrix = get_sample_sparse_matrix(train_sparse_data, 400, 40)
Sample Sparse Matrix for the test data:
test_sparse_matrix_matrix = get_sample_sparse_matrix(test_sparse_data, 200, 20)
Featuring the Data
Featuring is a process to create new features by adding different aspects of variables. Here, five similar profile users and similar types of movies features will be created. These new features help relate the similarities between different movies and users. Below new features will be added in the data set after featuring of data:

def create_new_similar_features(sample_sparse_matrix):
global_avg_rating = get_average_rating(sample_sparse_matrix, False)
global_avg_users = get_average_rating(sample_sparse_matrix, True)
global_avg_movies = get_average_rating(sample_sparse_matrix, False)
sample_train_users, sample_train_movies, sample_train_ratings = sparse.find(sample_sparse_matrix)
new_features_csv_file = open("/content/netflix_dataset/new_features.csv", mode = "w")
for user, movie, rating in zip(sample_train_users, sample_train_movies, sample_train_ratings):
similar_arr = list()
similar_arr.append(user)
similar_arr.append(movie)
similar_arr.append(sample_sparse_matrix.sum()/sample_sparse_matrix.count_nonzero())
similar_users = cosine_similarity(sample_sparse_matrix[user], sample_sparse_matrix).ravel()
indices = np.argsort(-similar_users)[1:]
ratings = sample_sparse_matrix[indices, movie].toarray().ravel()
top_similar_user_ratings = list(ratings[ratings != 0][:5])
top_similar_user_ratings.extend([global_avg_rating[movie]] * (5 - len(ratings)))
similar_arr.extend(top_similar_user_ratings)
similar_movies = cosine_similarity(sample_sparse_matrix[:,movie].T, sample_sparse_matrix.T).ravel()
similar_movies_indices = np.argsort(-similar_movies)[1:]
similar_movies_ratings = sample_sparse_matrix[user, similar_movies_indices].toarray().ravel()
top_similar_movie_ratings = list(similar_movies_ratings[similar_movies_ratings != 0][:5])
top_similar_movie_ratings.extend([global_avg_users[user]] * (5-len(top_similar_movie_ratings)))
similar_arr.extend(top_similar_movie_ratings)
similar_arr.append(global_avg_users[user])
similar_arr.append(global_avg_movies[movie])
similar_arr.append(rating)
new_features_csv_file.write(",".join(map(str, similar_arr)))
new_features_csv_file.write("\n")
new_features_csv_file.close()
new_features_df = pd.read_csv('/content/netflix_dataset/new_features.csv', names = ["user_id", "movie_id", "gloabl_average", "similar_user_rating1",
"similar_user_rating2", "similar_user_rating3",
"similar_user_rating4", "similar_user_rating5",
"similar_movie_rating1", "similar_movie_rating2",
"similar_movie_rating3", "similar_movie_rating4",
"similar_movie_rating5", "user_average",
"movie_average", "rating"]) return new_features_df
Featuring (adding new similar features) for the training data:
train_new_similar_features = create_new_similar_features(train_sample_sparse_matrix)train_new_similar_features.head()

Featuring (adding new similar features) for the test data:
test_new_similar_features = create_new_similar_features(test_sparse_matrix_matrix)test_new_similar_features.head()

Training and Prediction of the Model
Divide the train and test data from the similar_features dataset:
x_train = train_new_similar_features.drop(["user_id", "movie_id", "rating"], axis = 1)x_test = test_new_similar_features.drop(["user_id", "movie_id", "rating"], axis = 1)y_train = train_new_similar_features["rating"]y_test = test_new_similar_features["rating"]
Utility method to check accuracy:
def error_metrics(y_true, y_pred):
rmse = np.sqrt(mean_squared_error(y_true, y_pred))
return rmse
Fit to XGBRegressor algorithm with 100 estimators:
clf = xgb.XGBRegressor(n_estimators = 100, silent = False, n_jobs = 10)clf.fit(x_train, y_train)

Predict the result of the test data set:
y_pred_test = clf.predict(x_test)
Check accuracy of predicted data:
rmse_test = error_metrics(y_test, y_pred_test)print("RMSE = {}".format(rmse_test))

As shown in figure 24, the RMSE (Root mean squared error) for the predicted model dataset is 99%. If the accuracy is lower than our expectations, we would need to continue to train our model until the accuracy meets a high standard.
Plot Feature Importance
Feature importance is an important technique that selects a score to input features based on how valuable they are at predicting a target variable.
def plot_importance(model, clf):
fig = plt.figure(figsize = (8, 6))
ax = fig.add_axes([0,0,1,1])
model.plot_importance(clf, ax = ax, height = 0.3)
plt.xlabel("F Score", fontsize = 20)
plt.ylabel("Features", fontsize = 20)
plt.title("Feature Importance", fontsize = 20)
plt.tick_params(labelsize = 15)
plt.show()plot_importance(xgb, clf)

The plot shown in figure 25 displays the feature importance of each feature. Here, the user_average rating is a critical feature. Its score is higher than the other features. Other features like similar user ratings and similar movie ratings have been created to relate the similarity between different users and movies.
Conclusion
Over the years, Machine learning has solved several challenges for companies like Netflix, Amazon, Google, Facebook, and others. The recommender system for Netflix helps the user filter through information in a massive list of movies and shows based on his/her choice. A recommender system must interact with the users to learn their preferences to provide recommendations.
Collaborative filtering (CF) is a very popular recommendation system algorithm for the prediction and recommendation based on other users’ ratings and collaboration. User-based collaborative filtering was the first automated collaborative filtering mechanism. It is also called k-NN collaborative filtering. The problem of collaborative filtering is to predict how well a user will like an item that he has not rated given a set of existing choice judgments for a population of users [4].
DISCLAIMER: The views expressed in this article are those of the author(s) and do not represent the views of Carnegie Mellon University, nor other companies (directly or indirectly) associated with the author(s). These writings do not intend to be final products, yet rather a reflection of current thinking, along with being a catalyst for discussion and improvement.
Published via Towards AI
Resources:
References:
[1] How retailers can keep up with consumers, McKinsey & Company, https://www.mckinsey.com/industries/retail/our-insights/how-retailers-can-keep-up-with-consumers
[2] How Netflix’s Recommendation System Works, Netflix Research, https://help.netflix.com/en/node/100639
[3] Recommendations, Figuring out how to bring unique joy to each member, Netflix Research, https://research.netflix.com/research-area/recommendations
[4] Collaborative Filtering, University of Pittsburgh, Peter Brusilovsky, Sue Yeon and Danielle Lee, https://pitt.edu/~peterb/2480-122/CollaborativeFiltering.pdf














