Statistical Forecasting of Time Series Data Part 4: Forecasting Volatility using GARCH

Last Updated on January 6, 2023 by Editorial Team

Author(s): Yashveer Singh Sohi

Data Visualization

In this series of articles, the S&P 500 Market Index is analyzed using popular Statistical Model: SARIMA (Seasonal Autoregressive Integrated Moving Average), and GARCH (Generalized AutoRegressive Conditional Heteroskedasticity).

In the first part, the series was scrapped from the yfinance API in python. It was cleaned and used to derive the S&P 500 Returns (percent change in successive prices) and Volatility (magnitude of returns). In the second part, a number of time series exploration techniques were used to derive insights from the data about characteristics like trend, seasonality, stationarity, etc. With these insights, in the 3rd part, the SARIMA class of models was explored.

In this article, the GARCH model is built to model the volatility in S&P 500 Returns. The code used in this article is from Volatility Models/GARCH for SPX Volatility.ipynb notebook in this repository

Table of Contents

1. Importing Data
2. Train-Test Split
3. GARCH Model
4. Volatility of S&P 500 Returns
5. Parameter Estimation for GARCH
6. Fitting GARCH on S&P 500 Returns
7. Predicting Volatility
8. Evaluating the Performance
9. Conclusion
10. Links to other parts of this series
11. References

Importing Data

Here we import the dataset that was scrapped and preprocessed in part 1 of this series. Refer part 1 to get the data ready, or download the data.csv file from this repository.

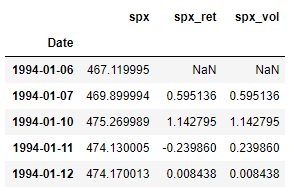
Since this is same code used in the previous parts of this series, the individual lines are not explained in detail here for brevity.

Train-Test Split

We now split the data into train and test sets. Here all the observations on and from 2019–01–01 form the test set, and all the observations before that is the train set.

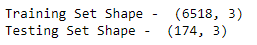
GARCH Model

GARCH stands for Generalized Auto-Regressive Conditional Heteroskedasticity. Conditional Heteroskedasticity is tantamount to conditional variance (or conditional volatility) in the time series. GARCH model uses the concept of volatility clustering to model the volatility of a series. Volatility Clustering essentially means that the volatility today, depends on the volatility at recent time steps. A GARCH model is specified using 2 parameters: GARCH(p, q). The GARCH model is formulated as shown below.

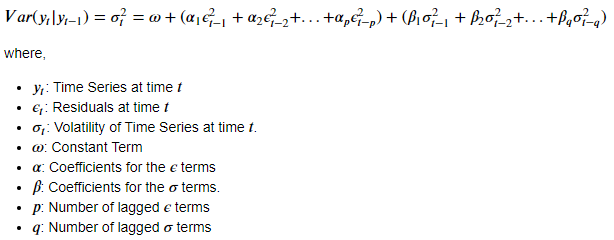
The above equation shows how GARCH models Volatility. The squared volatility at some time step is represented as the linear combination of some constant, a group of past residual terms, and a group of past volatility terms. The parameters p, and q are used to control the number of these lagged residual, and volatility terms in the above equation respectively.

Volatility of S&P 500 Returns

In this article, the Volatility of S&P 500 Returns is modeled using GARCH. In order to test whether the volatility predicted matches the volatility of returns in future, we calculate the magnitude of S&P 500 Returns and have stored it in the series spx_vol .

Thus, the model is fit on spx_ret series, and the predicted volatility is compared with spx_vol .

Parameter Estimation for GARCH

The PACF (Partial Auto-Correlation Function) plot is used to get an initial estimate of the parameters: p and q of the GARCH model. The number of significant lags in this plot is used as the initial parameters. Then the model summary table (displayed after fitting the model) is used to understand which coefficients in the model are significant. Based on this, the model is fine tuned.

Now, the PACF plot for S&P 500 Returns is generated:

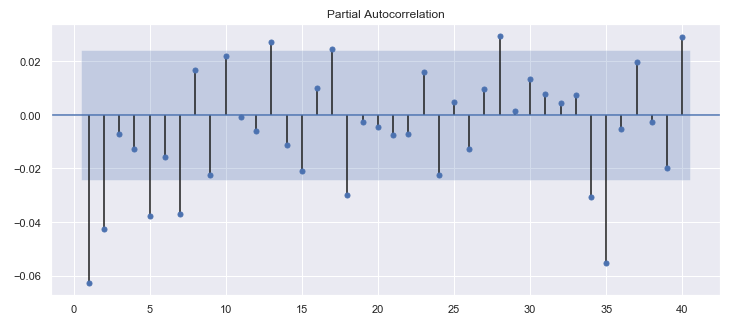
Using the plot_pacf() function in statsmodels.graphics.tsaplots package, the PACF plot is generated for the spx_ret series. On examining the plot, the first 2 lags are significant. Therefore, the GARCH(2, 2) model is suitable for an initial starting point.

Fitting GARCH on S&P 500 Returns

Now, a GARCH(2, 2) model is fit on the S&P 500 Returns series.

The arch_model() function in the arch package is used to implement the GARCH model. The Implementation mentioned here is inspired from the one mentioned in the official documentation here. Before fitting the model, a new dataframe is prepared. This dataframe consists of all the time steps in the original dataset (before train-test split). The training time steps are occupied by the Returns of S&P 500. These are actually used for training the GARCH model. The testing periods are occupied by the Returns observed one time step previously. This is tantamount to saying that the model will forecast tomorrow’s volatility in returns using the returns observed today.

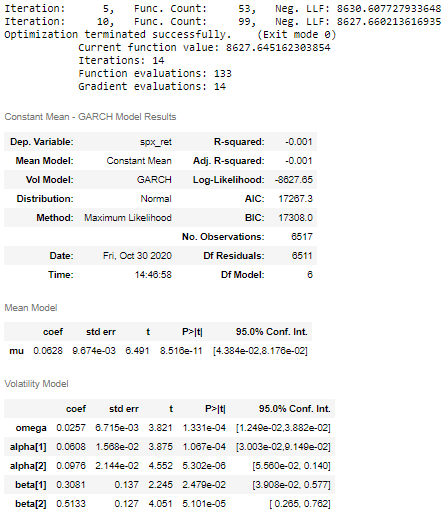
Using the arch_model() method, the model is defined. The function takes in the dataset mentioned above as input, and the parameters: p=2, and q=2 . The vol= “GARCH” argument specifies that the model to be used is GARCH. The model definition is stored in the variable model and the fit() method is called on it to train the model. The last_obs argument is used to ensure that the model is trained on train data only. The fitted model is stored in model_results variable, and the summary of this is displayed by calling the summary() on the fitted model.

The first few lines before the summary table in the output image shows the fitting information as displayed after each iteration by the fit() function. The update_freq=5 argument in the fit() function limits this information to be displayed after every 5 iterations. Next, in the summary table there are 3 sections: Constant Mean — GARCH Model Results, Mean Model, and Volatility Model. In the section for Volatility Model, the P<|Z| column clearly indicates that all the coefficients are significant at the 5% confidence level.

Predicting Volatility

Here the fitted model is used to forecast the volatility of S&P 500 Returns in the test set.

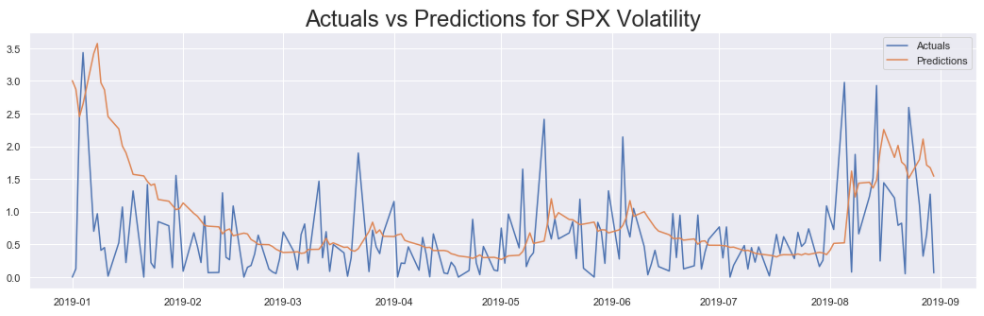
The forecast() method is used on the fitted model: model_results . This outputs an ARCHModelForecast object that contains the predictions for the mean model, and the volatility model. Next, the residual_variance attribute is called to get the predictions for volatility. The predictions are stored in a dataframe with the same number of periods as in data . All the periods on which the model is trained has NaN values in them, and only the periods for which the model should generate forecasts are actually populated. In this case, all the periods of the test set has real valued numbers, and the ones of the train set has NaN’s. The predictions are then plotted against the volatility (magnitude of returns) calculated heuristically.

Evaluating the Performance

The image above shows that whenever the predicted volatility of the model spikes violently, the magnitude of returns (heuristically calculated volatility) also fluctuates greatly. On the other hand, when the predicted volatility is stable, then the magnitude of returns are also relatively stable. Thus our model is clearly able to identify periods of high and low volatility in S&P 500 Returns.

The primary purpose of this model is to identify periods where the market is stable and periods where the market is volatile, and the model is successful in capturing this information. Thus, there is no reason to evaluate the model on error metrics like RMSE (Root Mean Squared Error)

Conclusion

In this article, the volatility in S&P 500 Returns was analysed and predicted using the GARCH model. In the next article, first, an ARIMA model will be used to fit the S&P 500 Returns. Then, a GARCH model will be used to model the residuals of ARIMA. This will allow us to generate much more reliable confidence intervals than the ones generated by the ARIMA model alone.

Links to other parts of this series

• Statistical Modeling of Time Series Data Part 1: Preprocessing
• Statistical Modeling of Time Series Data Part 2: Exploratory Data Analysis
• Statistical Modeling of Time Series Data Part 3: Forecasting Stationary Time Series using SARIMA
• Statistical Modeling of Time Series Data Part 4: Forecasting Volatility using GARCH
• Statistical Modeling of Time Series Data Part 5: ARMA+GARCH model for Time Series Forecasting.
• Statistical Modeling of Time Series Data Part 6: Forecasting Non — Stationary Time Series using ARMA

References

[1] 365DataScience Course on Time Series Analysis

[2] machinelearningmastery blogs on Time Series Analysis

[3] Wikipedia article on GARCH

[4] ritvikmath YouTube videos on the GARCH Model.

[5] arch documentation for forecasting using GARCH model.

---

Statistical Forecasting of Time Series Data Part 4: Forecasting Volatility using GARCH was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI