From Data to Dollars: Using Linear Regression

Author(s): Roli Trivedi

Originally published on Towards AI.

Unraveling the Magic Behind Predictive Analytics

Data-driven decision-making has become a game-changer for businesses in every industry. From optimizing marketing strategies to predicting customer behavior, data holds the key to unlocking untapped opportunities. In this article, we will be exploring the incredible potential of using Linear Regression as a powerful tool to convert data insights into tangible financial gains and the maths behind it.

Linear Regression is a supervised machine learning method to predict the relationship between dependent var(Y) and independent var(X) values.
Example, Stock Price Prediction

Types of Linear Regression

1. Simple Linear Regression: Here you have one input column and one output column.
2. Multiple Linear Regression: Here you have multiple input columns and one output column.
3. Polynomial Linear Regression: If the data is not linear then we used it.

Assumptions in Linear Regression

1. The relationship between the dependent variable and the independent variable is linear
2. There is little or no multicollinearity between the variables
3. Assumes it to be in the normal distribution form.

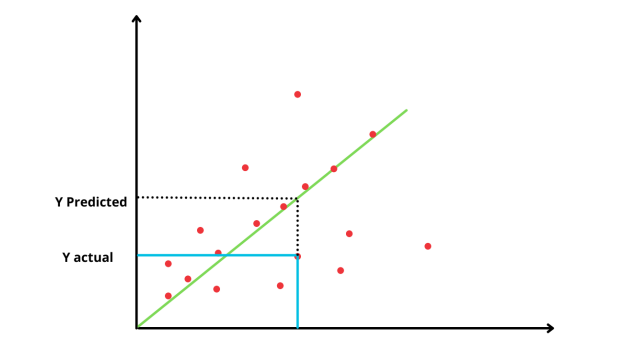
The main aim is to find the best-fit line which will describe the relationship between the independent variable and dependent variable by obtaining the line which has the minimum error.

Best fit line: It is the line that crosses maximum points and the distance between the actual points and the line is minimum.

But how will we find what is the best line to use?

We start with a horizontal line that cuts through avg of the value of data is probably the worst fit of all but it gives us a starting point to talk about how to find an optimal line to data.
For this horizontal line, x = 0
Since y = mx+c and x = 0. Therefore y = c (worst case because here y doesn’t depend on our dependent variable)
In the next step, we will find the sum of the squared residuals(SSR) for this line.

Sum of Squared Residuals (SSR)= It is the distance from the line to the data which is squared and then added up to find the SSR value. Residual is another word for Error.

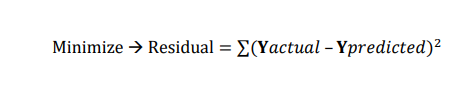
We aim to find the minimum SSR. Therefore we will rotate our horizontal line and concerning the new line we will find SSR. And we will keep doing it for different rotations.

Among all these SSR we got we will consider the minimum one and will use that line to fit our data. So the line with the least square is imposed on the data therefore this method is known as least squares.

Different Algorithms of Linear Regression

1. Ordinary least squares(OLS)
2. Gradient Descent : This is optimization technique

Evaluation metrics for Linear regression

• Mean Absolute Error (MAE): It is not differentiable. It keeps the unit same when trying to find MAE which makes it easy to interpret data and is robust to outliers.

• Mean Squared Error (MSE): It is differentiable but interpretation gets touched as the unit changes because we are squaring the unit here.

• Root Mean Squared Error(RMSE):

Interpretability : MAE>RMSE>MSE
Sensitive to Outliers: MSE>RMSE>MAE

• R-squared (R2): It is the coefficient of determination or goodness of fit. It checks how good is our best-fit line in comparison to the worst line. The value of R2 varies from 0 to 1. The more your model will move towards perfection the more the R2 value will move towards 1 and the more it will move towards the worst then the R2 value will move more towards 0.
  It tells us how much of variation in the y variable can be explained by the x variable.

R2 = Explained Variation/Total Variation
R2 = (Total Variation — Unexplained Variation)/ Total Variation
R2 = 1- (unexplained variation/total variation)
Here, Total Variation = Variation(mean) : (data-mean)²/n
Unexplained variation = Variation(fit) : (data-line)²/n

For Example, you want to predict the weight_lost and you have the calories_intake variable. If you get R2 as 70%, it means 70% of the variation in the marks variable can be explained with the help of the hours_studied variable. It has an accuracy of 70% which is goodness of fit.
Now if we add a new feature sleeping_hours and this doesn’t have much impact on the target variable i.e. not correlated with the weight lost. But if we calculate R2 again it will increase even if the new feature we added is not related. But this is not correct because it is increasing the accuracy of the model when in reality it is not and also we are increasing the computing power as we have to train one extra column which is not even required.

Problem with R2: Even though the features involved in the model won’t be so important still the R2 value will increase even if it increases by small number but it will increase it is never going to decrease. So even though R2 should not have been increased because the feature added is not important so we have to train the model unnecessarily. So we need to penalize this and therefore we have ‘Adjusted R2'

• Adjusted R2: Now imagine you are increasing more features in your model so your R2 value will be increasing because SS(res) value will always be decreasing. So Adjusted R2 comes into the picture which basically penalizes the attributes which are not correlated. So if my attributes aren’t correlated then only it will decrease my R2 value otherwise it will be increasing.

Adjusted R2 = 1- ((1-R2)(N-1)/N-P-1)
N = no of data points
P = no of independent features

Therefore adjusted R2 increases only when the independent variable is significant and affects the dependent variable. Also overfitting won’t happen because we are penalizing the value here.

Thanks for reading! If you enjoyed this piece and would like to read more of my work, please consider following me on Medium. I look forward to sharing more with you in the future.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI