Deep Hashing for Similarity Search

Last Updated on January 26, 2021 by Editorial Team

Author(s): Rutuja Shivraj Pawar

DEEP LEARNING, COMPUTER VISION

An overview of the novel deep hashing neural networks from the literature

In recent years Approximate Nearest Neighbor (ANN) [1] search has become a prominent topic of research to effectively process the ever-increasing amount of data in real-world applications. ANN has a variety of applications including Pattern recognition, Recommendation Systems, Similarity Search, Cluster Analysis, etc. However, in this article, we will focus primarily on the application of Similarity Search. Further, among the existing ANN techniques, Hashing has become effectively popular in the management, storage, and processing of high-dimensional data due to its fast query speed, and low memory costs [2–10].

A hashing model takes an input data point (images, document, etc.) and outputs a sequence of bits or hashcode representing that data point. Further, the taxonomy of the different hashing models based on their fundamental properties is as depicted below,

In this article, we will focus mainly on Data-Dependent Hashing, where the hash function is learned taking into account the input data distribution. The representative methods in this category include the Learning To Hash (L2H) [11–13] methods.

L2H [12, 13] is a set of data-dependent hashing methods that aim to learn a compact and similarity-preserving bitwise representation with shorter hash codes in such a way that similar inputs are mapped to nearby binary hash codes. Specifically from the different L2H methods, we will dive deep into Deep Hashing. Deep Hashing constitutes supervised L2H utilizing Deep Learning and comprises of different hashing methods, of which some of the novel ones concerning similarity search on image data along with their different functional design aspects are further elaborated upon,

Deep Pairwise-Supervised Hashing (DPSH)

Li et al. [14] propose a novel deep hashing method called Deep Pairwise-Supervised Hashing (DPSH) which does simultaneously feature learning and hash-code learning using supervised pairwise labels in an end-to-end architecture utilizing a feedback mechanism to learn better hash codes.

This end-to-end learning framework for image retrieval as seen in the above Fig., has three key components, the first component is a Convolutional Neural Network (CNN) to learn image representation from pixels, the second component is a Hash Function which maps the learned image representation to hash codes and the third component is a Loss Function which measures the generated hash code in comparison with the pairwise labels.

Triplet-based Deep Hashing

Inspired by Li et al.’s work on DPSH, Wang et al. [15] propose a novel Triplet-based Deep Hashing method (a special case of ranking labels) which simultaneously performs image feature and hash code learning in an end-to-end manner aiming to maximize the likelihood of the input triplet labels. This method experimentally evaluates to outperform the deep hashing based on
pairwise labels and pre-existing triplet label based deep hashing methods.

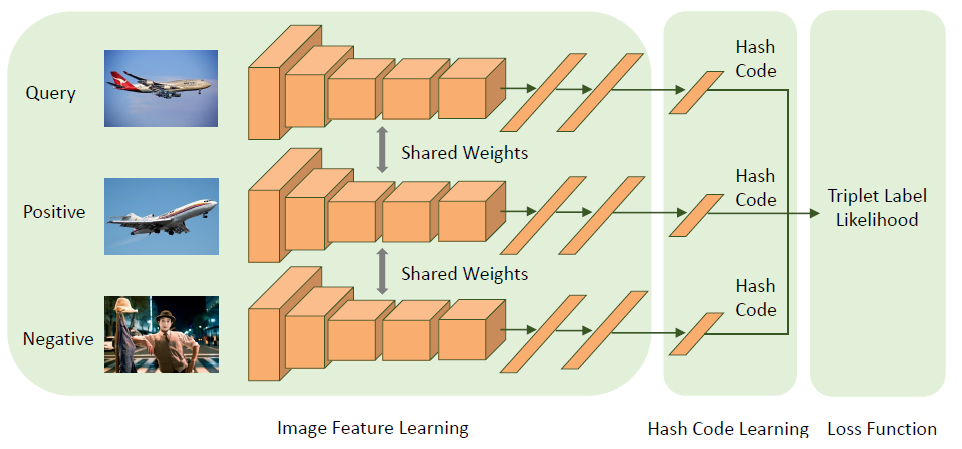
This end-to-end learning framework, as seen in the above Fig., has three components, a Deep Neural Network to learn features from images, one fully-connected Layer to learn hash codes for, from these features, and the Loss Function.

Objective Function

Latent Factor Hashing (LFH)

Regarding the objective function to learn similarity-preserving hash codes, Zhang et al. [16] were the first to proposes a supervised hashing method, Latent Factor Hashing (LFH) to learn similarity-preserving binary codes based on latent factor models and which can be efficiently used to train large-scale supervised hashing problems. LFH models the likelihood of pairwise
similarities as a function of Hamming Distance between the corresponding points. However, the optimization of this objective function is a discrete optimization problem that is not easy to solve, and hence this constraint is relaxed by transforming the discrete codes to continuous which might not achieve satisfactory performance [10].

Hence deep hashing methods utilizing LFH propose novel strategies to solve this discrete optimization problem in a discrete way, thus improving accuracy as in DPSH [14]. Wang et al. [15] in triplet-based deep hashing rather solve this discrete optimization problem in a continuous way as proposed by Zhang et al. [16], but consider the quantization error induced by this relaxation in the loss function.

Loss Function Optimization

Deep Hashing Network (DHN)

Regarding an optimized loss function for pairwise supervised hashing, Zhu et al. [17] propose a novel Deep Hashing Network (DHN) architecture that can simultaneously optimize pairwise cross-entropy loss on the learned semantic similar pairs and the pairwise quantization loss on the learned hash codes. This serves as an advantage towards better similarity-preserving learning and controlling the quality of the learned hash codes.

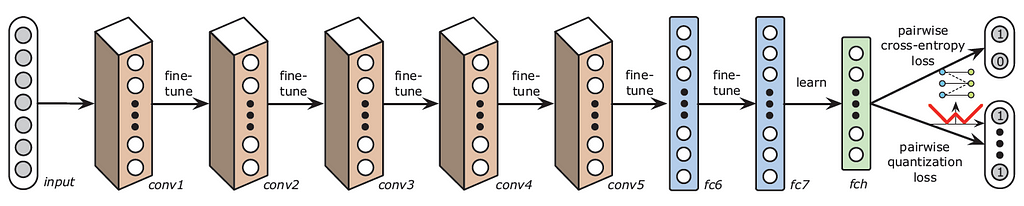
The pipeline architecture of DHN as seen in the above Fig., consists of four key components, the first component is a Subnetwork constituting of multiple convolution-pooling layers to learn image representations, the second component is a fully-connected Hashing Layer to generate compact hash codes, the third component is the pairwise cross-entropy Loss Function, and the fourth component is the pairwise quantization Loss Function.

Deep Supervised Discrete Hashing (DSDN)

Li et al. [18] propose a novel deep hashing method Deep Supervised Discrete Hashing (DSDN) which uses both pairwise label and classification information to generate discrete hash codes in a one stream framework. The optimization process keeps this discrete nature of the hash codes to reduce the quantization error and thus an alternating minimization method is derived to optimize the loss function.

The insights shared in this article are part of the systematic literature review carried out for the scientific research work An Evaluation of Deep Hashing for High-Dimensional Similarity Search on Embedded Data.

References

[1] A. Andoni and P. Indyk, “Near-optimal hashing algorithms for approximate nearest neighbor in high dimensions,” Communications of the ACM, vol. 51, no. 1, p. 117, 2008.

[2] B. Kulis and K. Grauman, “Kernelized locality-sensitive hashing for scalable image search.,” in ICCV, vol. 9, pp. 2130–2137, 2009.

[3] Y. Gong, S. Lazebnik, A. Gordo, and F. Perronnin, “Iterative quantization: A procrustean approach to learning binary codes for large-scale image retrieval,” IEEE transactions on pattern analysis and machine intelligence, vol. 35, no. 12, pp. 2916–2929, 2012.

[4] W. Kong andW.-J. Li, “Isotropic hashing,” in Advances in neural information processing systems, pp. 1646–1654, 2012.

[5] W. Liu, J. Wang, R. Ji, Y.-G. Jiang, and S.-F. Chang, “Supervised hashing with kernels,” in 2012 IEEE Conference on Computer Vision and Pattern Recognition, pp. 2074–2081, IEEE, 2012.

[6] M. Rastegari, J. Choi, S. Fakhraei, D. Hal, and L. Davis, “Predictable dual-view hashing,” in International Conference on Machine Learning, pp. 1328–1336, 2013.

[7] K. He, F. Wen, and J. Sun, “K-means hashing: An affinity-preserving quantization method for learning binary compact codes,” in Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2938–2945, 2013.

[8] G. Lin, C. Shen, Q. Shi, A. Van den Hengel, and D. Suter, “Fast supervised hashing with decision trees for high-dimensional data,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1963–1970, 2014.

[9] F. Shen, C. Shen, W. Liu, and H. Tao Shen, “Supervised discrete hashing,” in Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 37–45, 2015.

[10] W.-C. Kang, W.-J. Li, and Z.-H. Zhou, “Column sampling based discrete supervised hashing,” in Thirtieth AAAI conference on artificial intelligence, 2016.

[11] Y. Gong, S. Lazebnik, A. Gordo, and F. Perronnin, “Iterative quantization: A procrustean approach to learning binary codes for large-scale image retrieval,” IEEE transactions on pattern analysis and machine intelligence, vol. 35, no. 12, pp. 2916–2929, 2012.

[12] W. Kong and W.-J. Li, “Isotropic hashing,” in Advances in neural information processing systems, pp. 1646–1654, 2012.

[13] J. Wang, W. Liu, S. Kumar, and S.-F. Chang, “Learning to hash for indexing big data — a survey,” Proceedings of the IEEE, vol. 104, no. 1, pp. 34–57, 2015.

[14] W.-J. Li, S. Wang, and W.-C. Kang, “Feature learning based deep supervised hashing with pairwise labels,” arXiv preprint arXiv:1511.03855, 2015.

[15] X. Wang, Y. Shi, and K. M. Kitani, “Deep supervised hashing with triplet labels,” in Asian conference on computer vision, pp. 70–84, Springer, 2016.

[16] P. Zhang, W. Zhang, W.-J. Li, and M. Guo, “Supervised hashing with latent factor models,” in Proceedings of the 37th international ACM SIGIR conference on Research & development in information retrieval, pp. 173–182, ACM, 2014.

[17] H. Zhu, M. Long, J. Wang, and Y. Cao, “Deep hashing network for efficient similarity retrieval,” in Thirtieth AAAI Conference on Artificial Intelligence, 2016

[18] Q. Li, Z. Sun, R. He, and T. Tan, “Deep supervised discrete hashing,” in Advances in neural information processing systems, pp. 2482–2491, 2017.

Deep Hashing for Similarity Search was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI