Convolutional Neural Networks for Dummies

Last Updated on July 23, 2020 by Editorial Team

Author(s): Daksh Trehan

Deep Learning, Computer Vision

A perfect guide to Convolution Neural Networks

A notification pops on your Social media handle saying, somebody uploaded a picture that might have you in it.

Boom! How did it happen?

This is the magic of Image Classification.

Convolution Neural Networks(CNN) lies under the umbrella of Deep Learning. They are utilized in operations involving Computer Vision. Nowadays since the range of AI is expanding enormously, we can easily locate Convolution operation going around us. These play an important role ranging from Facebook Automatic Tagging, Face Unlock, OCR to driverless cars.

Image Classification takes an input(image in this case) and outputs a class/probability of that input belonging to a particular class with the help of a Deep learning algorithm i.e. CNN.

Why CNN?

According to the Universal Approximation theorem, Deep Neural Networks are powerful function approximators. And to the best, these can improve their accuracies using Backpropagation.

But due to the employment of so many parameters, Deep Neural Network often is very sensitive to overfitting that can even lead to the Gradient Vanish issue because of long chains. Additionally, Deep Neural Networks can’t handle variations such as translation, rotation, illuminations in images.

Therefore, to tackle this problem we developed a Deep Learning algorithm: Convolution Neural Network.

Image Classification

How do humans observe an image?

We have mastered our brains to determine objects quickly.

Now, how does it happens?

There are certain features that our brain relates an object to. Like for illustration, you were given an orange and an orange-colored ball. Both are identical, but still, the brain can accurately distinguish them, as we have trained it that surface of ball might be smooth but that of orange fruit is little rough.

Now for many years, we have trained our brains to differentiate between objects precisely. And same is the idea behind CNN i.e. to train our model to learn features from images.

How does a computer observes an image?

When we observe an image, we scrutinize various aspects, like edges of objects, the color of an object because we have been trained to do so from our childhood.

But, when we input an image to our model, for it, it is nothing but a collection of matrices.

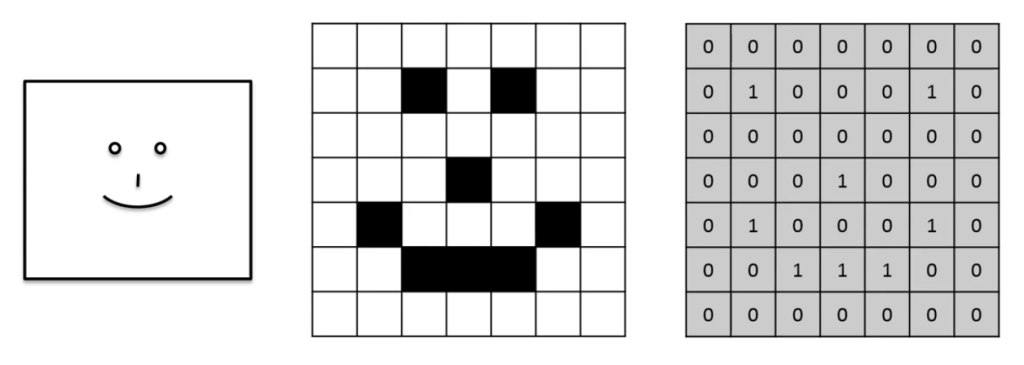
For our model, an image is a matrix of pixels. If we pass a colored image it will be a 3D array with RGB channels ranging from 0 to 255 if we pass black and white image, then we will get a 2D array with binary values.

So, when we talk about classification, we want our model to accurately define these variations so that, the output we get is as minutiae as possible.

For every feature, we have a different matrix representing its characteristics.

How CNN works?

The basic pipeline for CNN is as follows:

• Input an image.
• Perform Convolution operation to get an activation map.
• Apply the pooling layer to make our model robust.
• Activation function(mostly ReLu) is applied to avoid non-linearity.
• Flatten the last output into one linear vector.
• The vector is passed to a fully connected artificial neural network.
• The fully connected layer will provide a probability for each class that we’re after.
• Repeat the process to get well defined trained weights and feature detectors.

Convolution Layer

Convolution filter sweeps out features from an image i.e. it tries to learn from an image. It computes a dot product between the filter value and the image pixel values to form a convolution layer.

The values in the filter matrix are updated every time backpropagation is implemented. However, the dimensions of the filter matrix are determined explicitly by the programmer.

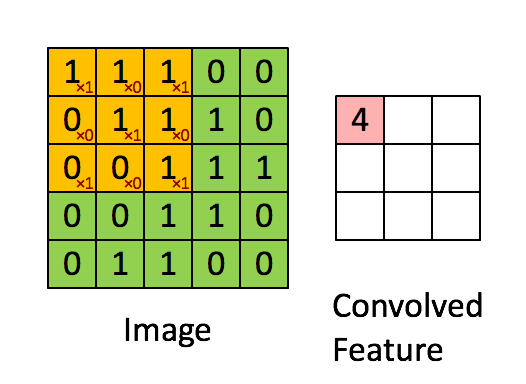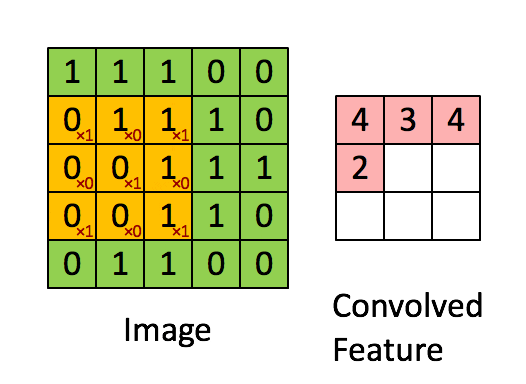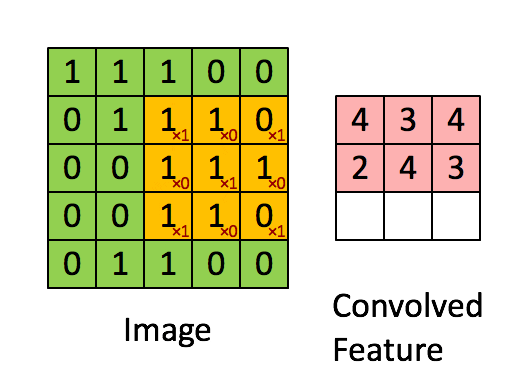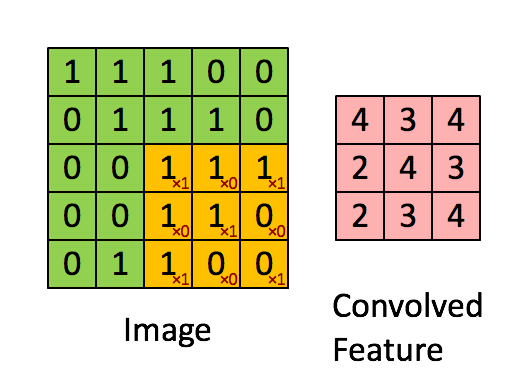
Each filter applied to 3D input will give a 2D output and by combining all those 2D outputs we get a 3D final output.

More the number of filters, the more the number of features learned by our model.

When we use the convolution filter, the dimensions of the output images are reduced to (h-f+1, w-f+1, c) from (h, w, c) and that is obvious because we can’t keep kernel at corners as it will cross input boundary.

To retain the dimensions of the output image, we use padding, in padding we follow adding zeros to every channel.

The bigger the kernel size, the larger the padding is required.

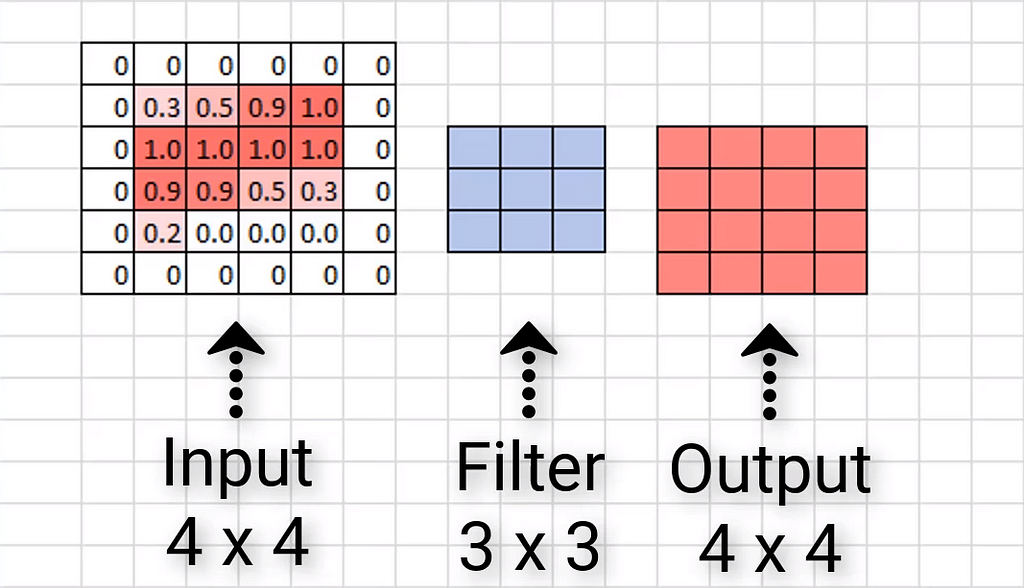
Alongside padding, we often employ stride. In convolution, to get an activation map we usually skip one pixel either downwards or sideward, but if we wish to skip custom numbers of pixel we can use stride.

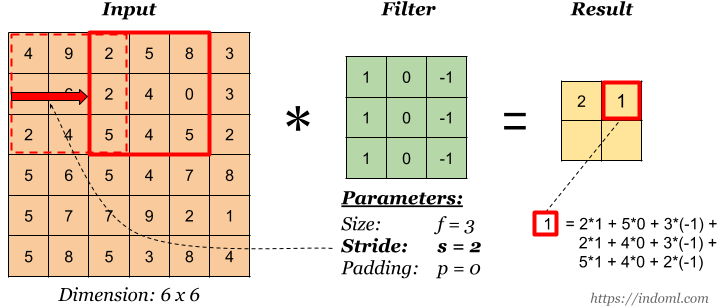
The more the stride, the less the output dimension.

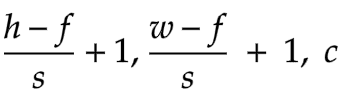
If we perform both stride and padding, the output dimensions would be:-

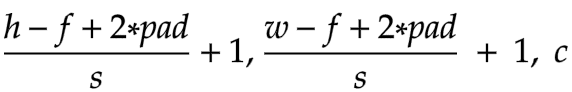
Pooling Layer

To create our model more robust and feature detector, CNN replaces output with a max summary to curtail data size and processing time. This allows the programmer to distinguish features with a higher impact.

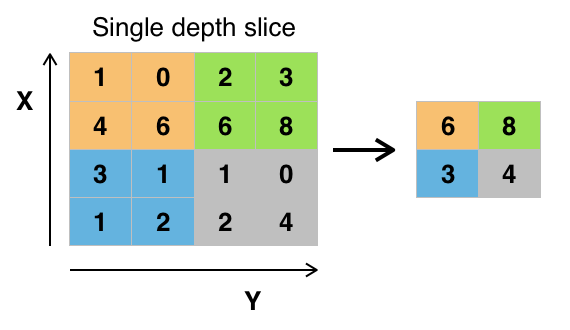
Max pooling takes two hyperparameters: stride and size. The stride will determine the number of values to be skipped and the size will determine the area of every skipped value pool.

Activation Function (ReLU and Sigmoid)

After applying convolution and pooling operation, activation functions are introduced to pertain nonlinearity for values x>0 and returns 0 if it does not meet the condition.

This method has been effective to solve diminishing gradient issues. Very small weights will remain as 0 after the ReLU activation function.

Fully Connected Layer

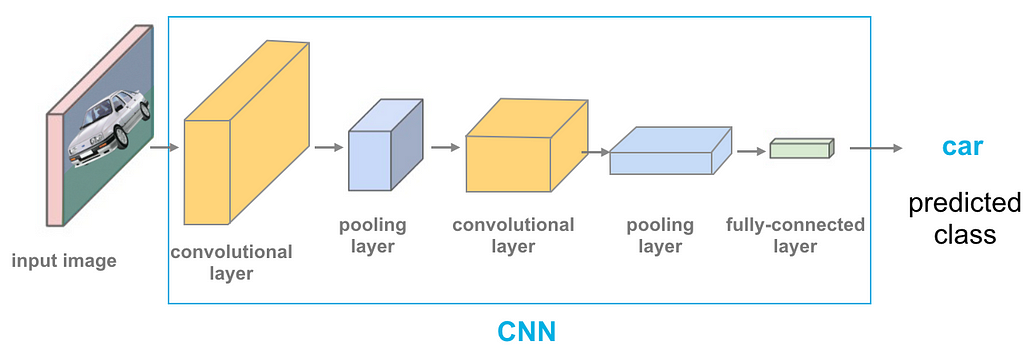
At this point, we are ready to add an artificial neural network to our convolutional neural network.

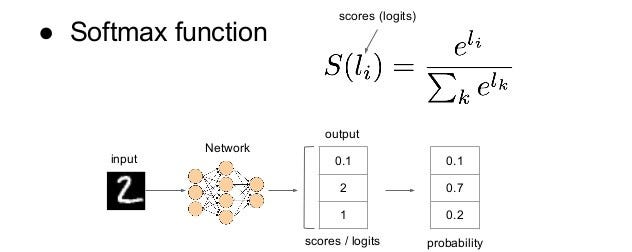
This is the final layer, we will input the flattened feature output to a column vector. To wrap up, we will feed our final flattened output to the softmax activation function that will assign a probability for each class. Every node in the previous layer is connected to the last layer and represents which distinct label to output.

How does CNN perform Backpropagation?

We use backpropagation to make our model learn better weights and biases to help optimize the performance of the model. This is a recursive process that helps our network to learn better.

Suppose, you have two output classes, one for a cat and another one for a dog. The cat neurons are certain, they will be triggered when some particular features like “whiskers”, “cat-iris”, “small and light body” are identified.

Through lots of iterations, the cat neuron learns that when certain features fire up, the image is a cat.

Similarly, dog neurons are active when some features like “big wet nose”, “floppy ears”, “heavy body” is triggered.

And as our model progress and it is trained recursively, now we can expect them to distinguish relevant and significant features for different classes, thus providing greater weight to those so that those characteristics can make a remarkable impact on our output.

Making CNN Better

Sadly, CNN is not perfect and is often immune to overfitting if not supervised in a proper manner.

Albeit, some of its issues can be resolved as discussed:

Dataset is relatively small

When the dataset is small, it is at ease to overfit. e.g. if you only show black dogs as dogs, then next time it wouldn’t recognize a white dog as a dog, because for our model the dog can be only black(which is obviously wrong and racist!)

Therefore, in such a case, it is advisable to artificially boost the diversity and number of training examples. One way of doing this is to add image augmentations and creating new variants. These include translating images and creating dimension changes such as zoom, crop, flips, shifts, etc.

Over Memorization

The more layers we have, the more the features are learned and this promotes memorization and inhibits generalize. The more you train your model, the more likely it becomes too specialized.

This can be avoided if we could reduce the complexity by removing a few hidden layers and neurons per layer. This technique is known as Dropout.

The idea is to drop some of the random neurons with every epoch, the final result would be average of all output.

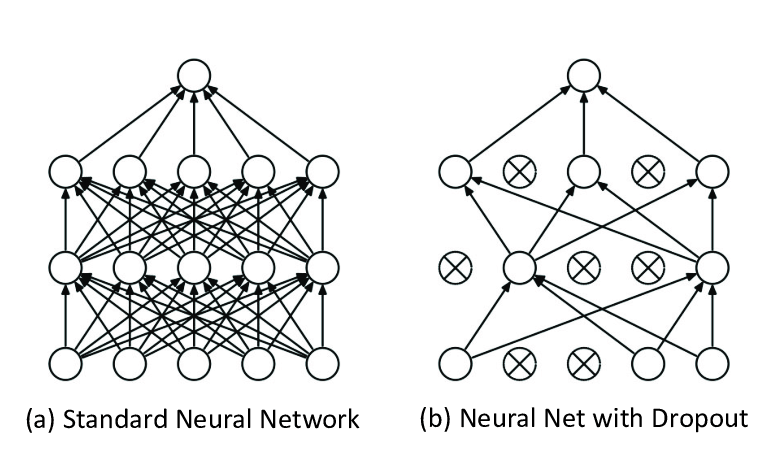
The neurons that aren’t participating in the computation function, their weights won’t be updated using backpropagation.

Conclusion

Hopefully, this article will help you to understand about Convolution Neural Networks in the best possible way and also assist you to its practical usage.

Please leave your suggestions and feedback. Just like you, I am still learning how to become a better Data Scientist and Engineer. Please help me improve so that I could help you better in my subsequent article releases.

As always, thank you so much for reading, and please share this article if you found it useful!

Feel free to connect:

LinkedIn ~ https://www.linkedin.com/in/dakshtrehan/

Instagram ~ https://www.instagram.com/_daksh_trehan_/

Github ~ https://github.com/dakshtrehan

Follow for further Machine Learning/ Deep Learning blogs.

Medium ~ https://medium.com/@dakshtrehan

Want to learn more?

Detecting COVID-19 Using Deep Learning

The Inescapable AI Algorithm: TikTok

Diving Deep into Deep Learning

An insider’s guide to Cartoonization using Machine Learning

Why are YOU responsible for George Floyd’s Murder and Delhi Communal Riots?

Why Choose Random Forest and Not Decision Trees

Clustering: What it is? When to use it?

Start off your ML Journey with k-Nearest Neighbors

Naive Bayes Explained

Activation Functions Explained

Parameter Optimization Explained

Gradient Descent Explained

Logistic Regression Explained

Linear Regression Explained

Determining Perfect Fit for your ML Model

Cheers!

---

Convolutional Neural Networks for Dummies was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI