Understanding Functions in AI

Last Updated on January 6, 2023 by Editorial Team

Last Updated on February 23, 2021 by Editorial Team

Author(s): Lawrence Alaso Krukrubo

Artificial Intelligence, Machine Learning

Exploring the Domain and Range of functions…

Every single data transformation we do in Artificial intelligence seeks to convert input-data to the most representative format required for the task we aim to solve… This conversion is done through functions.

A machine-learning model transforms its input data into meaningful outputs. A process that is “learned” from exposure to known examples of inputs and outputs.

Thus, the ML-model “learns a function” that maps its input data to the expected output.

f(x) = y_hat

Therefore, the central problem in Machine learning and Deep learning is to meaningfully transform data: In other words, to learn useful representations of the input data at hand — representations that get us closer to the expected output… (Francois Chollet)

Let’s look at a toy example…

We have a table of a few data points, some belong to a “white” class and others to a “black” class. When we plot them, they look like this…

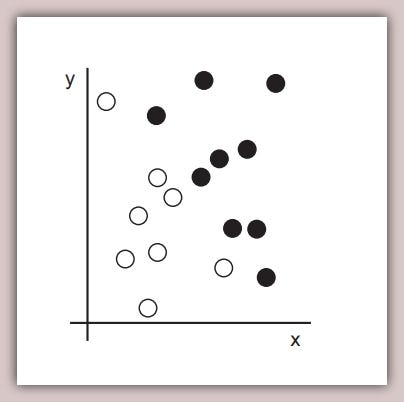
As you can see, we have a few black and white points. Let’s say we want to train an ML algorithm that can take the coordinates (x,y) of a point and output whether that point is black (class 0) or white (class 1).

We need at least 4 things

• Input data in this case the (x,y) coordinates of each point
• The corresponding outputs or target (black or white)
• A way to measure performance, say a metric like accuracy.
• An algorithm that befits the task, say of type Logistic Regression.

Ultimately, what we need here, from the model is a new representation of our data that cleanly separates the white points from the black points. Period!

This new representation could be as simple as a coordinate change or as complex as applying polynomial or rational or a combination of logarithmic, trigonometric and exponential functions to out data.

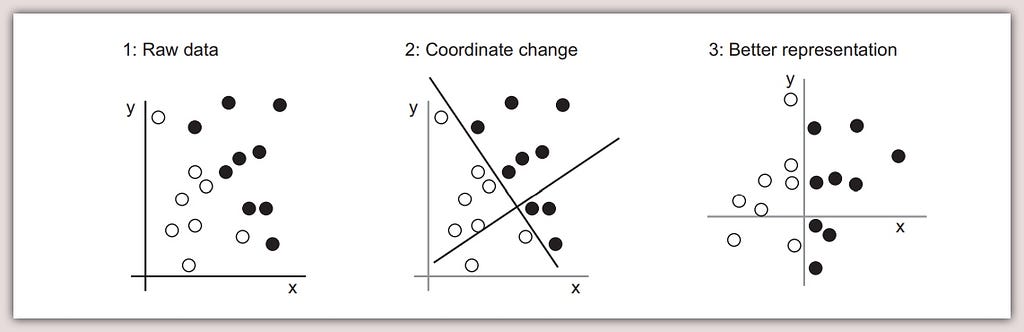
Let’s assume that after some optimisation and a stroke of luck, our algorithm learns the 3rd representation above which satisfies the rule:

{Black Points have values > 0, White points have values ≤ 0}

This means our model has learnt a representation of our data that can be denoted by a ‘function’ ( f of x, written as f(x)), that maps the input data to output target such that:

f(x) = 0 (‘Black’, if x > 0)

f(x) = 1 (‘White’, if x ≤ 0)

With this function, hopefully, the model would be able to generalize to classify future unseen data of black and white points.

So What The Heck is a Function Really?

Imagine you’re at a courier office in Florida U.S, sending a parcel x, to a location in Sydney Australia… The agent enters the parcel’s weight Wx and the distance Dx from Florida to Sydney and writes you a charge C, of $500.

This simply means the charge C of $500, is a function of the distance Dx and the weight Wx of the parcel x.

Let’s further assume the cost calculator simply applies a hidden function H, to the distance and the weight of any parcel, to arrive at a charge.

This entire transaction can be written as a function f(x) such that:

f(x) = H(Dx, Wx)

In other words, C given x is the result of a function f(x), that takes a hidden function H, which applies some computation to Dx and Wx.

This is the same as:

C = H(Dx, Wx)

Which is the same as:

$500 = Hidden_function(Distance-of-parcel-x, Weight-of-parcel-x)

So the notion of functions is ubiquitous and functions are everywhere around us. We can represent several constructs through functions. For example, it can be said that…

Having a good life is a function of healthy living and wealth

If we denote h for healthy-living and w for wealth, and x for good-life, we can non-trivially write this relationship as:

f(x) = h + w

A bit of Calculus…

Calculus is the mathematics that describes the changes in Functions…

The functions necessary to study Calculus are:-

1. Polynomial,
2. Rational,
3. Trigonometric,
4. Exponential, and
5. Logarithmic functions

Without going any deeper into Calculus, let’s see the definition of a function:

A function is a special type of relation in which each element of the first set(domain) is related to exactly one element of the second set(range).
For any function, when we know the input, the output is determined, so we say that the output of a function is a function of the input.

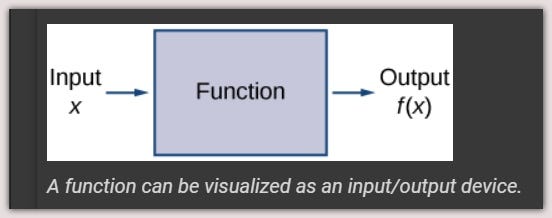
For example, the area of a square is determined by its side length, so we say that the area (the output) is a function of its side length (the input).

For any function, when we know the input, and the rule, the output is determined, so we say that the output of a function is a function of the input.

This simply means any given function f consists of a set of inputs (domain), a set of outputs (range), and a rule for assigning each input to exactly one output.

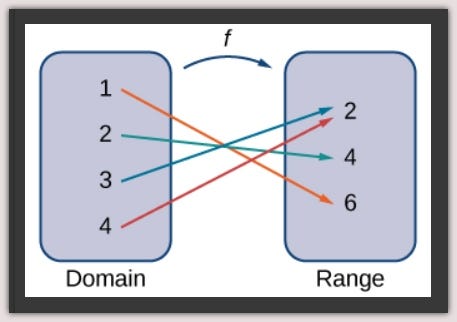
A function maps every element in the domain to exactly one element in the range. Although each input can be sent to only one output, two different inputs can be sent to the same output (see 3 and 4 mapped to 2 above).

Real, Natural and Negative Numbers:

Let’s quickly refresh our knowledge of the above, as it’s impossible to perform any activity in AI, without numbers…

1. Real Numbers:

The set of real numbers is the set of numbers within negative-infinity to infinity.

In interval-notation, it can be written as x is a real number if x is within:

(-inf, inf): less than neg-infinity and less than infinity

In set-notation:

{x|-inf < x < inf}: x, given that -inf < x < inf

The set of Real numbers is a super-set of all kinds of numbers, from fractions to floats to negative and positive numbers of arbitrary sizes.

2. Natural Numbers:

The set of natural numbers is the set of positive numbers from range(0, infinity)

In interval-notation:

[0, inf): includes 0 but less than infinity.

In set-notation:

{x|0≤ x}: x, given that 0 ≤ x

3. Negative Numbers:

The set of negative numbers is the set of all numbers less than 0

In interval-notation:

(-inf, 0): Less than neg-infinity and less than 0.

In set-notation:

{x|x < 0}: x, given that x < 0

Exploring The Domain and Range of Functions:

Given a certain function, how can we determine it’s domain and range? How can we figure out what legal inputs such a function can take and what legal outputs it can produce?

Function One:

f(x) = max(0,x)

The above expression means, for any given input of x, the function returns the maximum value between 0 and x.

With no further constraints, we can assume that x is any given number such that:

{x|-inf < x < inf}: meaning x is any real number.

Therefore the domain of this function is the set of Real-Numbers. And, since the output of this function is a minimum of 0 and maximum of any given number, we can denote the range of this function as the set of Natural-Numbers [0, inf) or {y|y ≥ 0}.

Plotting The Function:

Let’s plot the above function using a range of numbers from -10 to 10

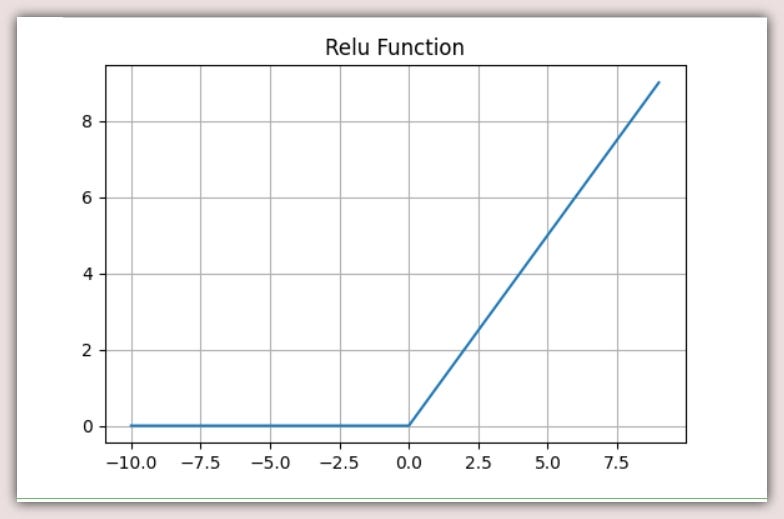
The function we’ve been exploring is the all popular Rectified-Linear-Unit. AKA Relu activation function. Relu is very simple, yet very powerful.

Perhaps the high-point of Relu is its successful application to train deep multi-layered networks with a nonlinear activation function, using backpropagation… Link

Function Two:

f(x) = sqrt(x + 3) + 1

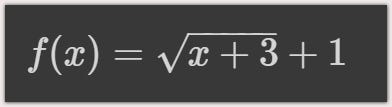
The above expression means, for any given input of x, the function returns the square root of (x + 3) + 1.

To find the domain, we need to pay attention to the rule of the function. Here, we have a square-root function as part of the rule. So that automatically tells us the expression within the square-root must have a minimum value of 0. Since we cannot find the square-root of negative numbers.

So to find the domain, we must ask… What value of x must we add to 3 to get a minimum of 0?

x + 3 = 0… Therefore: x = -3

Therefore the domain of the function is {x| x ≥ -3}, or [-3, inf).

With the rule and the domain, we can easily find the range. If we plug in the minimum value of -3 as x. Then the function would evaluate to sqrt of 0, which is 0, plus 1, which is 1. Therefore the range is [1, inf) or {y|y ≥ 1}.

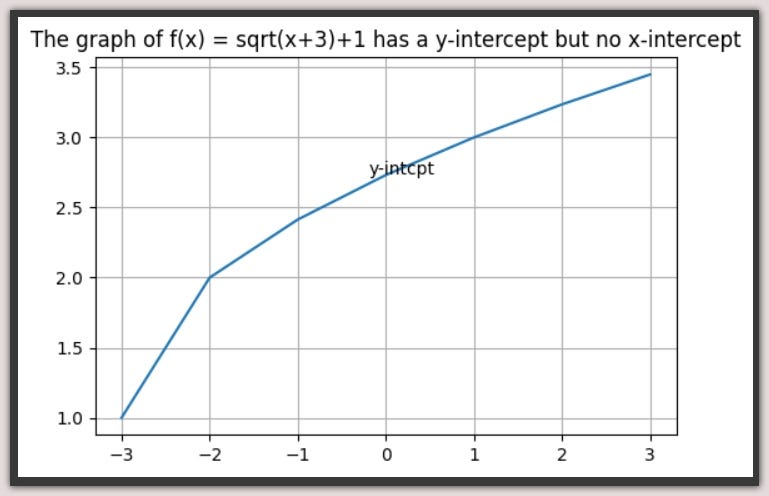
For any function, when we know the input, and the rule, the output is determined, so we say that the output of a function is a function of the input.

Function Three:

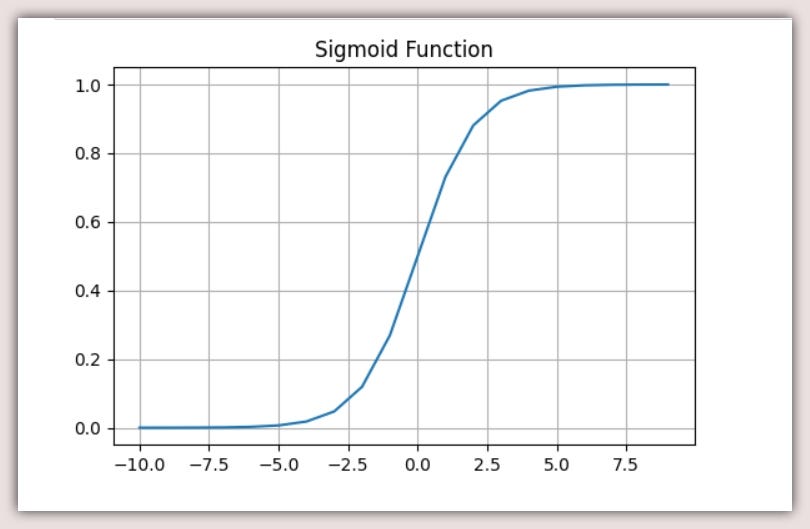
f(x) = 1 / (1 + e^-x)

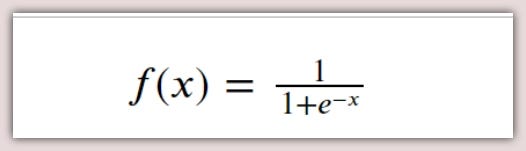
The above expression means, for any given input of x, the function returns 1/(1 + e, raised to negative x), where e is the Euler's number = 2.71828.

So how do we figure the domain of this function?

Looking at the function, we can see that x is actually the exponent, whose base is e. Therefore x can actually take any value regardless. This is because the domain of an exponential function is actually the set of all real numbers, as long as the base is not 0 and != 1.

So what about the range?

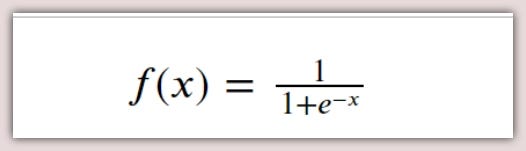
Understanding that the domain can take any value, leads us to the rule. The first thing we notice is the exponent of negative x. Since the exponent of 0 is 1, the exponent of a negative number must be within [0, 1).

So, if the exponent part returns 0, we get 1 / (1 +0) = 1. If it returns any other value v, where 0 < v <1, we get 1 / (1 + v) => some value (0, 1).

Therefore the range is (0, 1] or {y|0 < y ≤ 1}

Yep! the function we’ve just explored is the Sigmoid-Activation-Function, which is the hat we place on a Linear-Regression function to convert it to a Logistic-Regression function fit for Binary-Classification tasks.

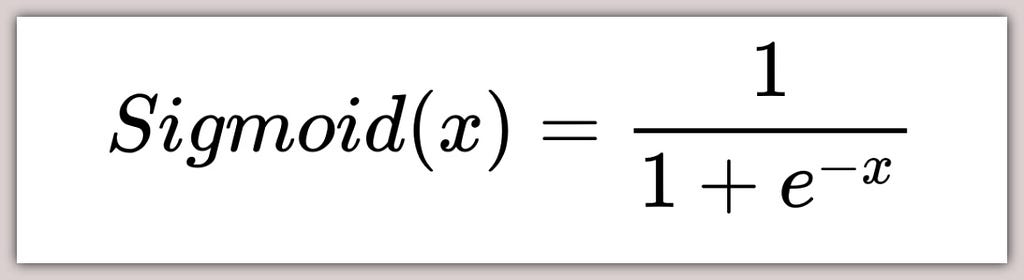
Plotting The Sigmoid:

More About The Sigmoid:

y_hat = w1x1 + w2x2 + b

The above equation denotes a multiple-linear-regression with 2 variables x1 and x2, multiplied with weights w1 and w2 plus bias b. If we convert y_hat from a continuous number like temperature, weight, and so on… To a discrete binary number like [0, 1] denoting two classes, we can simply apply the Sigmoid function to y_hat, set a threshold like 0.5 to demarcate both classes, and we have a fully functional Logistic-Regression model (log_reg).

log_reg = Sigmoid(y_hat)… => Sigmoid(w1x1 + w2x2 + b)

Furthermore, we can easily extend the Sigmoid function to the Softmax function.

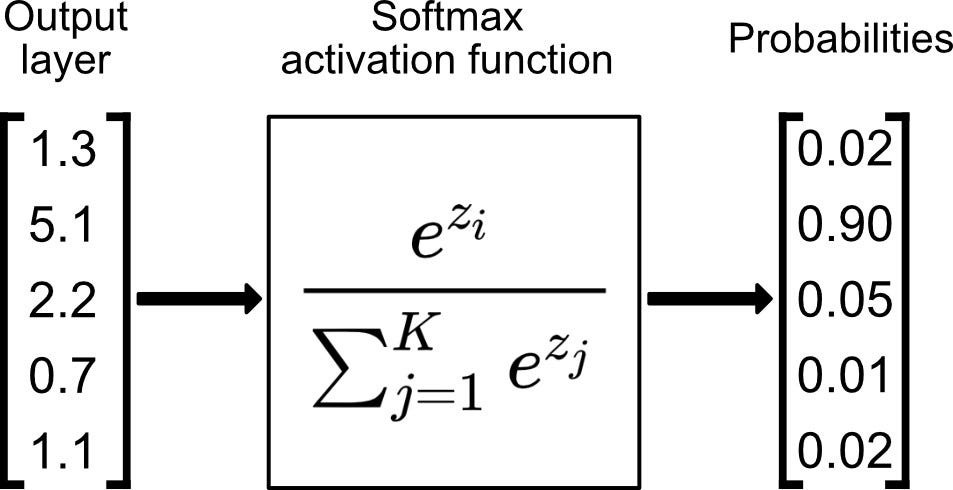
Softmax is ideal for multi-class classification. In softmax, we compute the exponent (e raised to [y1, y2…y5]) for each output class.

If we have 5 classes, we have a vector of 5 elements, [y1, y2 … y5]

So, we add up all the exponents and divide each exponent by the total sum of exponents. This gives 5 distinct probabilities adding up to 1.0. The value with the highest probability score becomes the prediction (y_hat)

Function Four:

f(x) = 3 / (x + 2)

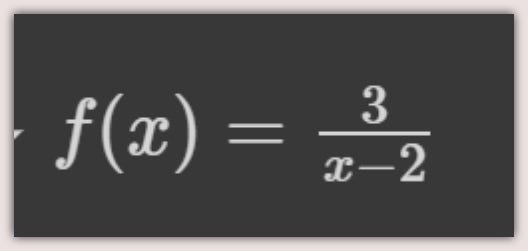
The above expression means, for any given input of x, the function returns the value of 3 / (x-2).

So yea, how do we determine the domain of this function? In other words, what values of x will make this expression valid?

Without any other constraints, x should be able to take on any Real-number except 2. This is because 3 / (2–2) is illegal and would raise a ZeroDivisionError.

Therefore the domain is (x != 2), or {x| x != 2}.

To find the range, we need to find the values of y such that there exists a real number x in the domain with the property that (3 / (x+2)) = y.

Since x can be any real number aside from 2. And 3 divided by (any real number plus 2) cannot be equal to 0.

Therefore the range is (y != 0) or {y| y != 0}.

Summary

The last example above was kinda tricky, but it follows the same general pattern of finding legal elements of the domain based on the rule. Then, mapping these elements to the range.

Functions are extremely important to programming in general and AI in particular. As we go about building models, importing libraries with lots of other functions or writing ours as need be. Let’s be conscious of the domain, rule and range of our functions. Attach a human-readable docstring to each function, except the name and variable names are so self-explanatory.

Thanks for your time.

Cheers!

Credit:

Deep learning with Python (Francois Chollet)

Montereyinstitute.org

Openstax.org

machine-learning mastery

About Me:

Lawrence is a Data Specialist at Tech Layer, passionate about fair and explainable AI and Data Science. I hold both the Data Science Professional and Advanced Data Science Professional certifications from IBM. and the Udacity AI Nanodegree. I have conducted several projects using ML and DL libraries, I love to code up my functions as much as possible even when existing libraries abound. Finally, I never stop learning, exploring, getting certified and sharing my experiences via insightful articles…

Feel free to find me on:-

Github

Linkedin

Twitter.

---

Understanding Functions in AI was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI