Evaluation-Time Bias in Evolutionary Algorithms

Last Updated on February 25, 2021 by Editorial Team

Author(s): Rutuja Shivraj Pawar

Artificial Intelligence, Optimization

A brief overview with the early research works from the literature

An Evolutionary Algorithm (EA) is a subset of evolutionary computation in artificial intelligence. Evolutionary computation is a family of algorithms for global optimization inspired by biological evolution. The rapid development of the information age with Big Data has led to an increase in the size and complexity of the optimization problems. In the context of an EA, this eventually results in the expansion of the search space with the fitness evaluation (used for optimal solution search) computation cost of the individuals becoming extremely high [1].

Diving deep into the EA variants, we observe the below different types,

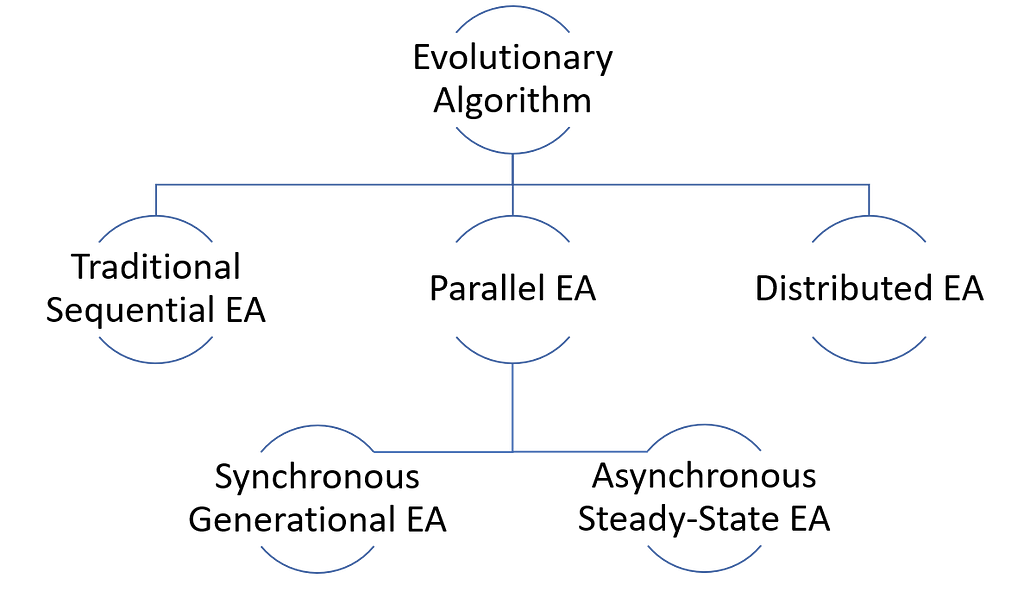
In this article, we will mainly focus on the Parallel EA variant with its two types and then dive deep into understanding the problem of evaluation time-bias.

Traditional generational EAs are derived from sequential EA but were formulated to induce parallelism [2]. However, these algorithms require synchronization and are often faced with the problem of idle time when there is time variance between the individuals to evaluate their fitness value. This often results in wastage of CPU resources and a hindrance to parallelization. To solve this problem we have asynchronous EAs [2] which are based on a steady-state model in which a one-at-a-time generation of an individual offspring takes place followed by their fitness evaluation. As soon as the fitness evaluation for an individual is completed, it can immediately compete for a place in the existing population without the need for synchronization. This process eventually helps in the effective utilization of computational resources and induces efficient parallel processing. However, asynchronous EAs are faced with the so-called problem of Evaluation-Time bias.

Evaluation-Time Bias [3] is the heritable phenomenon in which individuals who quickly evaluate themselves as compared to the other individuals in the population have a reproductive advantage in an EA. This eventually puts the long-evaluating individuals at a disadvantage since the fast-evaluating individuals have more opportunity to generate offsprings. This also leads to the solution search biased towards the fast-evaluating regions and away from the long evaluating regions of the search space and thus resulting in a premature convergence. However, sometimes evaluation-time bias can prove helpful in an algorithm if all the faster-evaluating individuals are better but at the same time can hinder the convergence if all of them are worse [4]. Noteworthily, in an experiment carried out in a flat fitness landscape, the evaluation showed no evidence of bias towards faster or slower regions, indicating that the bias may be small or negligible under certain conditions [2]. As a solution and depending on the scenario, sometimes penalizing high-quality solutions by assigning them with long-evaluation times can help to prevent the premature convergence of the EA and improve its performance [5].

Below illustrated are two early research works carried out towards solving the problem of evaluation time-bias and laid the foundations for further research directions,

Quasi-Generational Asynchronous Evolutionary Algorithm (QGEA)

QGEA [6] combines some aspects of synchronous and asynchronous EA as a novel algorithm for the best of both worlds. This proposed algorithm serves as an intermediate solution that would neither incur idle time nor significant bias towards fast solutions. QGEA utilizes the asynchronous evaluation scheme to evaluate the individuals in the population which minimizes idle time. However, evaluated individuals are not added directly into the parent population. Instead, a separate child population is created and they are added there one-at-a-time. Once the full capacity of the child population is reached, it replaces the parent population, and a new child population is then created. The difference between this algorithm and the traditional EA lies in the fact that it generates more children from each set of parents, which further helps in keeping all the processors occupied. The changes to the population occur in a generational way with complete replacement of the population after every defined-number of steps.

Evolutionary Algorithm with Interleaving Generations (IGEA)

IGEA [4] is equivalent to the standard generational EA but allows for better utilization of the computational resources by interleaving the fitness evaluations from different generations, thus avoiding the evaluation time bias and exhibiting a better parallelization potential. The main idea of the algorithm lies in the fact that some individuals from the next generation can be generated before the current generation is completely evaluated. Instead of incurring the CPU idle time as in a standard EA, IGEA tries to eliminate this through the evaluation of the generated individuals by the idle CPUs and thus does not require the processor nodes to wait until the slower evaluating individuals have completed their evaluation. There are two variants of IGEA, the comma version (λ, λ) and the plus version (λ + λ). The comma version has a population of λ and in each generation generates λ offspring to be used in the next generation. The plus version generates λ offspring from λ parents, then λ individuals from the combined offspring and parent population are selected for the next generation.

However based on their experimental evaluation both of the early approaches exhibit certain limitations, The QGEA approach does not solve the problem of evaluation-time bias as well as exhibits a very low convergence rate. The IGEA approach is not based on the asynchronous EA scheme and hence does not exhibit evaluation-time bias. The interleaving of the generations can only work when the selection of the individuals does not require all of the individuals to be evaluated before the execution. Hence, the IGEA approach aims to eliminate the problem of evaluation-time bias by interleaving the generations of the standard generational EA, but at the same time does not allow for the use of unlimited parallelism like the asynchronous EA’s.

More recently in the last year, we had two more research works published in this area. A new parent selection strategy to reduce the effect of evaluation-time bias by taking into account the search progress of each solution is proposed in [7]. This proposed method when experimentally evaluated using asynchronous NSGA-III [8], helps to reduce its computing time and the effect of evaluation-time bias. Another research work [9] builds on IGEA [4] and proposes a solution focussed on improving the CPU utilization through the concept of precedence evaluation of tentative offspring in IGEA.

Summarizing, as observed from the literature, there is no concrete solution identified towards the total elimination of the evaluation time bias. Hence the research on efficient methods for the effective elimination of the problem of evaluation-time bias in asynchronous EAs and the study on the open research question to predict how evaluation-time bias will affect an EA’s performance given a particular problem type and conditions remains a hotspot topic of research.

References

[1] Gong, Y.J., Chen, W.N., Zhan, Z.H., Zhang, J., Li, Y., Zhang, Q. and Li, J.J., 2015. Distributed evolutionary algorithms and their models: A survey of the state-of-the-art. Applied Soft Computing, 34, pp.286–300.

[2] Scott, E.O. and De Jong, K.A., 2015, January. Understanding simple asynchronous evolutionary algorithms. In Proceedings of the 2015 ACM Conference on Foundations of Genetic Algorithms XIII (pp. 85–98).

[3] Scott, E.O. and De Jong, K.A., 2015, July. Evaluation-time bias in asynchronous evolutionary algorithms. In Proceedings of the Companion Publication of the 2015 Annual Conference on Genetic and Evolutionary Computation (pp. 1209–1212).

[4] Pilát, M. and Neruda, R., 2017, July. Parallel evolutionary algorithm with interleaving generations. In Proceedings of the Genetic and Evolutionary Computation Conference (pp. 865–872).

[5] Yagoubi, M., Thobois, L. and Schoenauer, M., 2011, June. Asynchronous evolutionary multi-objective algorithms with heterogeneous evaluation costs. In 2011 IEEE Congress of Evolutionary Computation (CEC) (pp. 21–28). IEEE.

[6] Scott, E.O. and De Jong, K.A., 2016, July. Evaluation-time bias in quasi-generational and steady-state asynchronous evolutionary algorithms. In Proceedings of the Genetic and Evolutionary Computation Conference 2016 (pp. 845–852).

[7] Harada, T., 2020, December. Search Progress Dependent Parent Selection for Avoiding Evaluation Time Bias in Asynchronous Parallel Multi-Objective Evolutionary Algorithms. In 2020 IEEE Symposium Series on Computational Intelligence (SSCI) (pp. 1013–1020). IEEE.

[8] Deb, K. and Jain, H., 2013. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints. IEEE transactions on evolutionary computation, 18(4), pp.577–601.

[9] Noguchi, H., Sonoda, A., Harada, T. and Thawonmas, R., 2020, September. Interleaving Generation Evolutionary Algorithm with Precedence Evaluation of Tentative Offspring. In 2020 59th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE) (pp. 832–837). IEEE.

Evaluation-Time Bias in Evolutionary Algorithms was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI