Initialization, BatchNorm, and LayerNorm: Beyond textbook definitions

Author(s): Adam Elimadi

Originally published on Towards AI.

There are a ton of blog posts out there breaking down both initialization and normalization. However, I feel like most authors fail to get into the apprentice’s shoe especially those that are complete beginners and at the same time picky learners that like digging into the “WHY” of everything. So, if you never heard of those terms before (or even did), I would still cover them but this time, we are going deep down the rabbit hole, tinkering with the very founding abstractions of these concepts and ultimately debunking a couple of widespread fallacies even amidst “experts”.

Spoiler Alert: I expect you guys to have a pen and a piece of paper in hand. This is going to be an active learning session and not any other dull read full of technical jargon fogging up your brain and making you question yourself. So, Bear with me!

Table of content:

I) Why initialization matters?

II) The deal

— 1. Random Initialization (noisy variance)

— 2. Good Initialization (stable variance)

— 3. Before vs After Comparison

III) Symmetry and Zero initialization

— 1. Symmetry

— — 1.1. Exercise 1

— 2. Zero Initialization

— — 2.1. Zero Initialization with ReLU and Tanh

— — — 2.1.1. Exercise 2

— — 2.2. Zero Initialization with Sigmoid

— 3. The importance of randomness

IV) Where do Initializations come from? (mathematical derivation)

— 1. Xavier Initialization

— 2. He Initialization

— — 2.1. Exercise 3

— — — 2.1.1. ReLU’s hard gating and selective behavior

V) Batch Normalization:

— 1. Batch Normalization is an extension of initialization

— 2. Computing statistics and using them to normalize our pre-activations

— 3. Affine Transformation

— — 3.1. What beta and gamma actually do?

— — — 3.1.1 Interactive visualization

— 4. Covariate Shift and its link to the affine transformation

— 5. Running averages

— 6. Pure implementation of BatchNorm’s forward pass

— 7. Related open-ended questions

VI) BatchNorm’s backward pass:

— How the gradient w.r.t the pre-normalized inputs impact params updates

— Mathematical derivation

— — Exercise 4

— Intuitive, raw implementation of the backward pass

VII) Layer Normalization:

— LayerNorm difference from BatchNorm

— How would that look in code

Conclusion

References

Why initialization matters?

If you may, I ‘ll start by recounting a personal anecdote.

One day, I was playing with logistic regression trying to run a classification task over a single neuron. I first initialized my only weight and bias to be random, and obviously it was rendering small values which didn’t work. Not to mention, I was getting a decision boundary curve totally baffling as it was misclassifying all datapoints, but the loss still decreased(somehow). Anyways, I later figured out that I put a minus instead of a plus in the cross-entropy loss. Even with that fixed, the results were still incredibly divergent, so I started tweaking the lr (learning rate), added L2 regularization etc. None seemed to be working until after couple of tests, I stumbled upon the perfect weight and bias. At that moment, I realized that I have to learn initialization techniques asap.

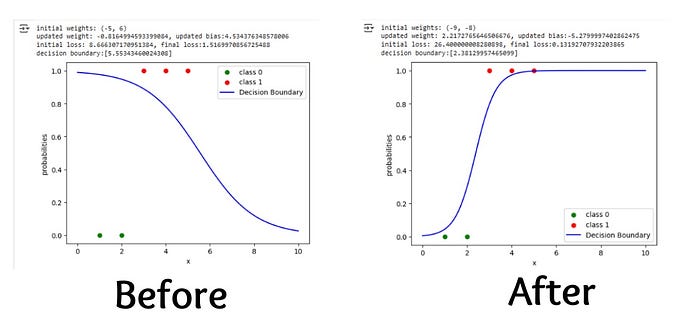
Here is the deal:

As you may have heard, initialization is simply assigning our parameters within a specific range following a certain distribution. This ensures stable activations in the forward pass, helping maintain smooth gradient flow in the backward pass and preventing the exploding or vanishing gradients problem, which ultimately speeds up the process of decreasing our loss.

Let's concretize this mambo-Jambo using basic math:

For that, we will train a tiny model from scratch using linear algebra with a bad initialization and a good one and then do a “before-and-after” comparison.

1.Random Initialization (noisy variance):

2. Good Initialization (stable variance):

3.Before VS After:

I know some of you may have their head aching over the steps involved in training the above explanatory model. Lucky for you, I only have good news.

First, you don’t have to worry about any of the technical jargon you just saw, and I only want you to focus on the activations and gradients' shift in magnitudes transitioning from a bad to a good initialization and how it impacted the loss.

Second, there is an upcoming blogpost on how to train models from scratch manually where you’ll learn everything you need to know to run forward and backward passes without any libraries and even on a piece of paper. So, stay on the lookout and eat good. Trust me, you’ll need every single bit of your cognitive prowess but it's worthwhile.

What is symmetry? And what does zero initialization have to do with it?

1. Symmetry:

Symmetry simply emphasizes the fact that if you instantiate a weight matrix with the same values, therefore, neurons, within each layer, will receive the exact same signals and hence, compute the same outputs.

So here is what’s going to happen:

• Each dense layer reduces to a single neuron, wasting compute and making training inconvenient.
• The model barely learns anything causing underfitting.
• The loss plateaus early on, and training will eventually stall.

So, similar values initialization is not only theoretically bad, but also empirically disastrous and shall crumble your training.

> Exercise 1:

You going to test that out yourself and witness how learning collapses due to symmetry. Here is the setup:

You have to rework the above model used to compare between good and bad initialization by changing the random weight matrices to constant-value weight matrices (e.g. [[5], [5], [5], [5]]). You can pick random distinct values of your choice for each of the weight matrices besides zero, as we going to cover that momentarily. Even though it is not required, I will advise you to set the bias vectors to zero for simplicity.

After you’re done with those little tweaks, all you have to do now, is follow the exact same computations above, but this time using the new weights. Got it?

2. Zero-Initialization:

Zero initialization also causes symmetry and conserves linearity in the machine’s learning, because it is obviously a constant-value initialization too. But what makes it different?

It is different because unlike other scalars, it will cause other training-related issues relative to widely adopted activation functions like ReLu, Tanh, and Sigmoid. Let’s break down what happens with each one of them:

ReLu / Tanh:

For ReLu and Tanh, our activations will always output zero (dead neurons), gradients will therefore null out, we’ll have no updates, and training will just halt before even starting.

> Exercise 2:

To experience that yourself, once again, take the above model’s parameters, set them to zero, run the same computations, and see chaos unfold.

Sigmoid:

Sigmoid activations will always render 0.5, no dead neurons but no diversification either and therefore we will have neurons stuck in a dead zone due to the lack of noise and stochasticity (symmetry paradox). Gradients will instantly die, and our training comes to an end.

Here are the activations formulas so you can test with them:

As you might have already concluded, akin to constant-value initialization, zero initialization introduces linearity causing symmetry in our neural network, in addition to zeroing out the gradients preventing any learning to take place at all.

In summary, the symmetry problem stems from the absence of random variables. And zero initialization is a more extreme case of symmetry where neurons are drawn to “off-states” leading to gradients going obsolete and hence, no training.

3. The importance of randomness:

You might be wondering: “Mr. Author, we just saw earlier that a random initialization is bad in practice, why are you saying that it is needed to fight against symmetry?”.

The randomness used to train the above neural net is derived from a naive initialization, meaning we just merely picked arbitrary values for our parameters taking nothing into consideration. For instance, when we use np.random.rand( ), we’re sampling from a uniform distribution in the range [0,1). Yes, that breaks symmetry, but it still doesn’t guarantee a smooth training with no noise, gradients’ oscillations, divergent activations and so on.

That’s when we turn the lights to initialization techniques. These methods, like Xavier or He initialization, offer thoughtfully designed distributions from which we sample our weights, giving us peace of mind knowing that the noise is moderate due to the zero-mean. This allows gradients to meaningfully explore the loss surface, ultimately leading to faster and more stable convergence, while controlling the variance to keep activations and gradients under control.

So, where do these initializations come from?

1. Xavier Initialization:

Xavier initialization is suitable for Sigmoid and Tanh activations. It imposes a variance that accounts for noise and fluctuations in both forward and backward pass, so we better keep it steady.

to derive this variance, we apply the following logic:

1) we know that: z = (x * w) * fan_in + b
fan_in: the number of input connections to a neuron in a given layer.

We multiply by fan_in because each neuron in layer k recieves a unique weight from
every k-1 layer neurons, resulting in fan_in repetitions of the term "z * w".

in order to achieve a stable variance among our activations, we need:
var(z)=var(x)

First, let's set the formula for var(z):
var(z) = var((x * w) * fan_in) 

NB: Note that b is left out as it's a constant and it dosen't affect the spread
of our variables, just their mean by shifting it either left or right.

Second, The variance of two vraibales is written as follows:
var((x * w) * fan_in) = fan_in * var(x * w) + 2*n*cov(Xi*Wi, Xj*Wj)

n: numbers of unique pairs of the two variables / cov(Xi*Wi, Xj*Wj): covariance

assuming that w and x are independent, that means covariance equals zero, thus:
var((x * w) * fan_in) = fan_in * var(x * w)

Third, let's write down the fromula for the variance of a product:
var(x * w) = var(x) * E[w]^2 + var(w) * E[x]^2 + var(x) * var(w)

E[w]: mean of W / E[x]: mean of X

now assuming that w and x are centered around 0 (zero mean), we conclude:
var(x * w) = var(x) * var(w)​

Fianlly, assuming that w and x are independent and zero-mean, we multiply
their variances and sum over the number of input neurons; fan_in:

var(z)= fan_in * var(w) * var(x)

in order for var(x) = var(z) to be true, we set n_in * var(w)=1
from that we conclude: var(w) = 1/fan_in

but we're not done yet, what about the backward pass?

2) we know that: dl/dx = w.T * dl/dz

in order to achieve a stable variance among our gradients, we need to ensure:
var(dl/dx)=var(dl/dz)

similary, assuming that w and dl/dz are independent and centered around 0 (zero mean), we multiply
their variances but this time we sum over the number of output neurons; fan_out, since the gradient
flow depends on the output layer.

var(dl/dx)= fan_out * var(w) * var(dl/dz)

so,in order for var(dl/dx) = var(dl/dz) to be true, we set fan_out * var(w)=1
from that we conclude: var(w)= 1/fan_out

3) Lastly, in order to account for both activations and gradients flow, we average through
both constraints. This ensures a stable variance across both passes:

var(w)= (1/fan_in + 1/fan_out )/2 ---> 2/(fan_in + fan_out)

NB: the final output of var(w) is not directly derived from the average,
but we used a clever heuristic (harmonic mean) to serve the same purpose. With one slight upgrade, that is:
this approximation is simpler and even more computationally practical.


Now, given that any given normal distribution is written as N~(mean,standard deviation):

we want our weights to be equally derived from both tails of zero, making sure
they don't bias activations in any direction. For that, we set the mean equal to zero. 

SD = sqrt(variance), therefore: SD = sqrt(2/(fan_in + fan_out))

Fianlly the normal distribution used to initialize our weights following Xavier's method 
is: N~(0 , sqrt(2/(fan_in + fan_out))

----------------------------------------------------------------------------

Next up: Uniform distribution and to your releif, it's a piece of cake.

We derive the uniform distribution from the normal one in such a way:

By definition var(U~(a,-a)) = a^2/3: We're essentially saying if a random varibale x is 
drawn from a uniform distribution on (-a,a), its variance is a^2/3.

In our case x is the weights W, so we write: var(w) = a^2/3

From 3), we know that var(w)= 2/(fan_in + fan_out). So, the equation becomes: 

 2/(fan_in + fan_out) = a^2/3

We need to conclude "a" which is our boundaries's threshold, thus:

 a = sqrt(6/(fan_in + fan_out))

Finally, we conclude that the uniform distribution for Xavier's initialization is:

 U~(-sqrt(6/(fan_in + fan_out)) , +sqrt(6/(fan_in + fan_out)))


A couple of side notes:

. the - a and +a in the uniform distribution refer the lower and upper bound, respectively.

. the mean is computed as u = -a+(+a)/2 which simplifies to zero in our case. Keep in mind that
 regradless of the distribution, centering your initialization at zero is crucial: it ensures 
 that pre‑activations are, on average, equally positive and negative. This balanced starting 
 point lets the network immediately explore all directions in the loss landscape, rather 
 than being biased toward one side.
 
. var(w)= (a- (-a))^2/12 which in this case simplifies to a^2/3

. As you might've noticed, the mean and variance across both distributions are conserved.

. The only difference is the spread and boundedness of the weights' values given a 
 normal distribution would still squash them into a controllable range and keep them 
 close to the mean but there is a risk of outliers. An issue that uniform distribution
 addresses and gives us that peace of mind ensuring that weights would never drift away
 from the defined bounds.
 

2. He Initialization:

He initialization is tailored for ReLu activations, it accounts for neurons going out of service (dead neurons).

> Exercise 3:

I guess, at this point, you know the drill; you’ll derive it yourself.

Here are some heads-ups:

First up, as we mentioned, we must account for the dead neurons resulting of negative weights values due to the sampling from a zero-mean distribution. To do that, we multiply by 1/2 in the forward pass’ var(z) formula. Because theoretically, on average, half of weight' values are negative and therefore half of neurons will just die.

Additionally, you don’t have to bother with averaging forward and backward pass variances when using He initialization, because ReLU is a form of “hard gating”. That means ReLU treats part of its input domain (zero and negative values) differently, making it inherently asymmetric.

Symmetry here would mean that all pre-activations’ values (weighted sums) are treated equally, but that’s not the case with ReLU. It blocks negative values from propagating any signal, effectively shutting off certain neurons. As a result, those neurons become dysfunctional, and this selective behavior is exactly what imposes asymmetry in the flow of information. Conversely, Tanh and Sigmoid don’t discriminate against negative values and process all inputs identically even if certain inputs might yield extremely small outputs in some cases.

Other than that, all you have to do is follow the exact same forward pass steps in the same order with the aforementioned instructs in mind.

If successful, here is what you should find:

That’s it for initialization and if you made it thus far, you deserve a small treat to pump you up and get you ready for what’s coming next.

As we’ve seen, initialization is crucial to our training, but it only helps control variance early on. Its effect fades as training progresses due to weight updates and non-linearities. This causes unstable activations and gradients. To fix this, we use dynamic normalization methods like BatchNorm and LayerNorm to maintain stable variance across layers and epochs.

Batch Normalization:

1.BatchNorm: An extension of Initialization

Batch Normalization is a further step of initialization that addresses the same core problem but more elegantly.

How so?

When BatchNorm is applied at each layer, here is what happens:

x → [Linear: W*x + b] → z → [BN: (z-μ)/σ] → z_hat→ [γ*z_hat + β] → y → [activation]

BatchNorm computes per-feature statistics of our pre-activations in each layer. Those statistics are leveraged to normalize our weighted sums implying a zero-mean and unit variance, which helps control our activations. But before we get there, there is one crucial step that precedes outputs’ computation: affine transformation and that is simply introducing two learnable parameters (gamma and beta) to scale and shift the normalized version of z that we shall call z_hat, giving the model the freedom to acquire any needed scale or offset evaluating whether normalization helps and how much. That process is repeated at every single layer with every single input throughout the entirety of our training, compensating for the gradual deterioration of initialization.

Now, let's dive into each part and dissect it:

2. How to compute statistics and use them to normalize our pre-activations:

Imagine we have batch size of 4 and a layer k has 2 neurons. the pre-activations matrix for that layer will have a shape of [batch size, number of neurons]. So, in this case, 4 rows and 2 columns, and we proceed to calculate the mean and variance column-wise.

Here is how:

Given pre-activation matrix X (shape: 4 x 2)

X =
[[ 0.5, -1.2],
 [ 1.3, 0.7],
 [-0.8, 2.1],
 [ 0.0, -0.5]]
--------------------------------------------------
Step 1: Compute per-feature (column-wise) means

mean_col1 = (0.5 + 1.3 + (-0.8) + 0.0) / 4 = 0.25
mean_col2 = (-1.2 + 0.7 + 2.1 + (-0.5)) / 4 = 0.275

Mean = [0.25, 0.275]

--------------------------------------------------
Step 2: Compute per-feature variances

var_col1 = [(0.5 - 0.25)² + (1.3 - 0.25)² + (-0.8 - 0.25)² + (0.0 - 0.25)²] / 4
 = [0.0625 + 1.1025 + 1.1025 + 0.0625] / 4 = 2.33 / 4 = 0.5825

var_col2 = [(-1.2 - 0.275)² + (0.7 - 0.275)² + (2.1 - 0.275)² + (-0.5 - 0.275)²] / 4
 = [2.1756 + 0.1806 + 3.3516 + 0.6006] / 4 = 6.3084 / 4 = 1.5771

Variance = [0.5825, 1.5771]

Now, we use the above-calculated statistics to normalize our weighted sums imposing a zero-mean and a unit variance. Therefore, we’ll be sampling from the following distribution: Z~N (0, 1)

Epsilon ensures that the denominator is never zero by adding a small constant to the variance which can be in certain cases close to zero.

Let’s carry on with the above example:

Step 3: Normalize each entry xij(i:row number, j: neuron number) using:
x̂ = (x - mean) / sqrt(variance + ε), with ε = 1e-5

Column 1 (Neuron 1):
x̂₁₁ = (0.5 - 0.25) / sqrt(0.5825) ≈ 0.25 / 0.763 ≈ 0.3275
x̂₂₁ = (1.3 - 0.25) / sqrt(0.5825) ≈ 1.05 / 0.763 ≈ 1.376
x̂₃₁ = (-0.8 - 0.25) / sqrt(0.5825) ≈ -1.05 / 0.763 ≈ -1.376
x̂₄₁ = (0.0 - 0.25) / sqrt(0.5825) ≈ -0.25 / 0.763 ≈ -0.3275

Column 2 (Neuron 2):
x̂₁₂ = (-1.2 - 0.275) / sqrt(1.5771) ≈ -1.475 / 1.256 ≈ -1.174
x̂₂₂ = (0.7 - 0.275) / sqrt(1.5771) ≈ 0.425 / 1.256 ≈ 0.338
x̂₃₂ = (2.1 - 0.275) / sqrt(1.5771) ≈ 1.825 / 1.256 ≈ 1.453
x̂₄₂ = (-0.5 - 0.275) / sqrt(1.5771) ≈ -0.775 / 1.256 ≈ -0.617

--------------------------------------------------
Final normalized matrix:

[
 [ 0.3275, -1.174 ],
 [ 1.376 , 0.338 ],
 [-1.376 , 1.453 ],
 [-0.3275, -0.617 ]
]

3. Affine Transformation:

After we normalize our pre-activations, we pass them through a linear transformation:

We initialize gamma to 1 and beta to 0 in BatchNorm to ensure that, the model begins training using the pure normalized output (zero mean and unit variance) without any learned distortion. By starting from this neutral configuration, the model can then learn, through gradient descent, how to adjust gamma and beta to scale and shift the activations in a way that improves performance. This approach preserves the benefits of normalization early on while allowing the network to later modify the distribution of activations as needed to enhance expressiveness.

So, what Gamma and Beta actually do?

Geometrically speaking, variance influences the speed of our gradients across the loss landscape, while the mean guides their direction. Imposing unit variance through normalization can sometimes be overly restrictive, dampening the model’s ability to make decisive moves toward the minima. Similarly, forcing a zero mean may misalign the gradient flow, especially in deeper layers where the network grows increasingly confident in its learned representations. As signals propagate deeper, the model begins to favor certain directions, and gradients reflect this bias. To accommodate and even encourage this behavior, we must allow the network to set a mean that aligns with its trajectory. The affine transformation step in Batch Normalization resolves these constraints: gamma scales the normalized activations to regulate gradient magnitude, while beta shifts them to guide the model’s focus, effectively restoring the network’s agency to navigate the loss landscape with both speed and intent.

I built this interactive simulation with Gemini where you can visualize how γ and β impact activations’ distribution and how does it influence the gradient’s navigation of the loss landscape.

4. Covariate Shift and how does it link to the affine transformation?

If you ever came across the original paper of BatchNorm, you’ll notice that the main thing authors claim to address with their algorithm is the Internal Covariate Shift.

ICS is simply the continuous change in the network’s activations distribution as parameters keep getting updated, exactly the downside we highlighted earlier about initialization techniques.

The truth is, ICS is not significantly reduced or mitigated at all, and that is not a bad thing as many people do think. In fact, it is actually healthy for deep neural nets.

To understand how and why, all we have to do is link the dots. We saw that a unit variance is good keeping activations in check, but the model might need a bit more freedom to learn all the features. This is when Gamma and Beta come into the picture, and they’re learned parameters for a reason:

Initially, they’re set to one and zero respectively to ensure activations will be purely sampled from a zero mean and unit variance distribution. Then, in the backward pass, we compute how the loss changes with respect to Gamma and Beta which mirrors how much does the normalization impact the loss in the first training step. The gradients with respect to γ and β reflect how much the network wants to stretch or shift the normalized activations. In effect, the model sculpts its own input distribution for each layer, not to suppress ICS, but to control and leverage it. And the same workflow persists at every single layer, every batch, and every epoch.

In conclusion, we can all agree that a moderate and controllable ICS is in fact lucrative and helps keep our activations stable while allowing informed statistical calibrations for better and faster learning.

5. Running averages:

We saw earlier, as part of BatchNorm’s operation during training, statistics (mean and variance) are computed column-wise in the current mini-batch. This means that BatchNorm’s performance depends on the batch size, the larger the batch, the more stable and accurate these statistics are.

However, during inference, we often process a single sample at a time, making it impossible to compute meaningful batch statistics.

To address this, BatchNorm maintains a running average of the mean and variance throughout training using an exponential moving average, think an approximation of global statistics. These accumulated statistics are then used during inference, ensuring consistent behavior even when the input batch is very small or contains only one sample.

6. Pure implementation of BatchNorm’s forward pass:

def forward_pass(x_batch, w_input, w_output, b_input, b_output, gamma, beta,training=True, epsilon=1e-5, batch_size=2,momentum=0.9):

 # weighted sum computation:
 z_input = np.dot(x_batch, w_input.T) + b_input

 if training:
 #Computing mini-batch statistics:
 mean = np.mean(z_input, axis=0)
 variance = np.var(z_input, axis=0)

 # Initialize and update running statistics:
 if not hasattr(forward_pass, 'running_mean'):
 forward_pass.running_mean = np.zeros_like(mean)
 forward_pass.running_var = np.ones_like(variance)

 forward_pass.running_mean = momentum * forward_pass.running_mean + (1 - momentum) * mean
 forward_pass.running_var = momentum * forward_pass.running_var + (1 - momentum) * variance

 else:
 mean = forward_pass.running_mean
 variance = forward_pass.running_var

 # Normalization:
 z_input_normalized = (z_input - mean) / np.sqrt(variance + epsilon)

 # Affine Transformation:
 z_input_hat = gamma * z_input_normalized + beta

 # Activation:
 z_input_activation = Leaky_Relu(z_input_hat)

 # Output:
 z_output = np.dot(z_input_activation, w_output.T) + b_output


 cache= (z_input_activation, z_output, z_input_normalized, mean, variance, z_input_hat, z_input)


 return cache

7. Q&A:

Now that we covered everything you need to know, let’s test your intuition by some thought-provoking follow-up questions.

I came across those open questions in a precious technical piece about BatchNorm, which I highly recommend as a follow-up read to this one.

The questions are as follows:

For the record, these questions are still deeply nuanced and have not been empirically verified yet. Feel free to ponder them as creatively as you can.

I’m going to go first and share my thoughts:

> Batch Normalization (BN) aids generalization mainly through normalization, which smoothens the loss landscape by stabilizing activations across batches. This results in more predictable gradients, helping the optimizer move more effectively through parameter space. While 𝛾 and 𝛽 don’t directly cause this smoothing, they play a key complementary role by restoring scale and shift after normalization. This preserves representational flexibility, prevents over-regularization, and allows gradients to explore richer feature directions, enhancing generalization.

> On the optimization side, normalization controls internal covariate shift, enabling the use of larger learning rates and leading to faster convergence. Gamma and Beta enhance this effect by ensuring that the network retains its ability to model complex patterns even in the presence of normalized activations.

> Regarding the long-term impact of BN on gradients, it’s important to note that BN’s behavior is closely tied to the weights that precede it. These weights determine the distribution of pre-normalized activations, which in turn affects the outcome of normalization. If the weighted sums are already close to zero-mean and unit variance, the normalization process becomes less disruptive, and the training dynamics more stable. This interdependency subtly shapes the optimization landscape, making it more navigable and aiding in consistent gradient flow over time.

BatchNorm’s Backward Pass:

This is arguably the most intimidating part of BatchNorm, and surprisingly, I’ve only found one technical blog post that actually covers it.

Let’s kick things off with a simple comparison to lay the groundwork for what’s coming next:

Imagine a vanilla regression model composed of a single neuron (for simplicity) with no non-linearities:

Forward Pass: z = w·x + b → linear activation → output = z

To compute gradients in the backward pass, we need ∂L/∂z, which in this case is straightforward to derive from z.

Now, consider a Batch-Normalized layer:

Forward Pass: z → BN: (z-μ)/σ → z_hat→ γ*z_hat + β → y → activation

Here, ∂L/∂z cannot be directly derived from z, because the weighted sum affects the loss through several components:

the normalized values (z_hat), the batch mean (μ), and the batch variance (σ²).

NB: Although γ and β are part of the forward pass, they are learned parameters that scale and shift ẑ and do not depend onz itself. Therefore, they do not lie on the gradient path from the loss back to z.

1. How the gradient w.r.t the pre-normalized inputs impact params updates:

During backpropagation, we must account for the normalization applied to the pre-activations. In a standard (vanilla) setting, we can compute ∂L/∂z directly, since the output depends linearly on z. However, with BatchNorm, the output depends on z indirectly, through the normalized version ẑ, which itself depends on the batch mean and variance. As a result, we must apply the multivariable chain rule to trace the effect of z on the loss via these intermediates.

From a training dynamics perspective, this gradient computation respects the normalization process. It allows updates to the weights via gradients that properly account for normalization effects, which gradually shape the distribution of pre-activations z to better align with the assumptions BatchNorm makes. This, in turn, reduces the burden on γ and β to correct extreme or erratic inputs, helping lower the loss and enabling more stable and effective feature learning.

2. Mathematical Derivation:

I figured this passage will be better off serving as a practice session of some Calculus namely the multivariable chain rule which is inevitable for ML pupils.

First, I recommend visiting the link above which contains an MIT’s brief break down of the topic.

As a general rule, for a variable x that impacts a loss L through multiple intermediate variables (y₁, y₂, ...):

In a BatchNorm setup, the pre-activations (z) impact the loss through the batch statistics (mean and variance) and the normalized inputs ẑ. Thus:

> Exercise 4:

As an exercise for this section, you shall wrestle with the derivative of each term in the chain rule. If successful, here is what you should get:

3. Intuitive, raw implementation of the backward pass:

def backward_pass(w_input, w_output, b_input, b_output, gamma, beta, x_batch, y_batch,
 cache,e, lr=0.001, batch_size=2, epsilon=1e-8):

 z_input_activation, z_output, z_input_normalized, mean, variance, z_input_hat, z_input = cache

 # Gradients for gamma and beta
 dz_input_hat = -2*e
 dgamma = np.sum(z_input_normalized * dz_input_hat, axis=0)
 dbeta = np.sum(dz_input_hat, axis=0)

 # Gradient through normalization
 dz_input_normalized = dz_input_hat * gamma
 dvariance = np.sum(dz_input_normalized * (z_input - mean) * -0.5 * (variance + epsilon)**(-1.5), axis=0)
 dmean = np.sum(dz_input_normalized * (-1/np.sqrt(variance + epsilon)), axis=0) + dvariance * (-2 / batch_size)*np.sum(z_input - mean, axis=0)
 dz_input = (dz_input_normalized/np.sqrt(variance + epsilon)) + (dvariance * 2 * (z_input - mean)/batch_size) + (dmean/batch_size)
 

 # Gradients for output layer
 deltas_output = -2 * e / batch_size
 dw_output = np.dot(deltas_output.T, z_input_activation) / batch_size
 db_output = np.sum(deltas_output, axis=0) / batch_size

 # Gradients for hidden layer
 dw_input = np.dot(x_batch.T,dz_input).T / batch_size
 db_input = np.sum(dz_input, axis=0) / batch_size
 

 # Parameter updates
 w_input -= lr* dw_input
 w_output -= lr * dw_output
 b_input -= lr * db_input
 b_output -= lr * db_output
 gamma -= lr * dgamma
 beta -= lr * dbeta

 return w_input, w_output, b_input, b_output, gamma, beta

Layer Normalization:

LayerNorm only differs from BatchNorm in statistics computation, same principle of normalization, but different axis of computation.

While BatchNorm computes mean and variance column-wise, LayerNorm, computes them row-wise across features of each sample.

Hence, no running averages are needed as we no longer rely on batch-size but rather on features number in each sample.

Here is what would change in code:

# Statistics Compuatation (in forward pass):

mean = np.mean(z_input, axis=1, keepdims=True) 
variance = np.var(z_input, axis=1, keepdims=True)

# Gradient through normalization (in backward pass) :

dz_input_normalized = dz_input_hat * gamma
dvariance = np.sum(dz_input_normalized * (z_input - mean) * -0.5 * (variance + epsilon)**(-1.5), axis=1,keepdims=True)
dmean = np.sum(dz_input_normalized * (-1/np.sqrt(variance + epsilon)), axis=1,keepdims=True) + dvariance * (-2 / batch_size)*np.sum(z_input - mean, axis=1,keepdims=True)
dz_input = (dz_input_normalized/np.sqrt(variance + epsilon)) + (dvariance * 2 * (z_input - mean)/batch_size) + (dmean/batch_size)

As you can see, every calculation that had (axis = 0) was replaced with (axis=1, keepdims = True).

You might be wondering what keepdims is used for:

• keeps the reduced axis as a dimension with size 1 instead of removing it after reduction.
• Facilitates broadcasting by maintaining a compatible shape for element-wise operations with the original tensor.
• Prevents shape mismatch errors when performing arithmetic like subtraction or division using the reduced results.

Example:

z_input = np.array([[1, 2, 3], [4, 5, 6]]) # shape (2, 3)

**With kepdims**

mean = np.mean(z_input, axis=1, keepdims=True) 
# mean = [[2], [5]] shape (2,1)
# subtract: z_input - mean 
# shape (2,3) - (2,1) → broadcasts mean to each feature in the row

**Without keepdims**

mean = np.mean(z_input, axis=1)
# mean = [2, 5] shape (2,)
# subtract: z_input - mean
# NumPy broadcasts (2), which will likely error out

Conclusion:

That was my first technical blog post ever. I hope that you guys found it to be engaging and that you actually learned something this time, as I tried to make it an active learning session as much as I could. If you still have any remaining questions, please don’t hesitate to comment them and I promise to make it my top priority to answer them all.

Next Up: Digging into the inner workings of deep neural networks.

We’ll learn the math behind training neural networks from start to finish and I’ll make sure that you’ll be able to train one manually from absolute scratch. This one will be extremely fun, so stay tuned 🙂

References:

[1] Ioffe, S., & Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift.

[2] Huber, J. (2020). Batch Normalization in 3 Levels of Understanding. Medium.

[3] MIT OpenCourseWare. (2010). Multivariable Calculus — Gradients and Optimization.

[4] Adam, E. (2025). ICS-BatchNorm: A study on Internal Covariate Shift and Batch Normalization [Source code]. GitHub.

[5] Adam, E. (2025). ICS-BatchNorm: Interactive Visualization. GitHub Pages.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI