![[AI/ML] Keswani’s Algorithm for 2-player Non-Convex Min-Max Optimization [AI/ML] Keswani’s Algorithm for 2-player Non-Convex Min-Max Optimization](https://miro.medium.com/v2/resize:fit:700/1*gtYIsACNBX9EvoDj3RyXkw.png)
[AI/ML] Keswani’s Algorithm for 2-player Non-Convex Min-Max Optimization
Last Updated on November 17, 2024 by Editorial Team
Author(s): Shashwat Gupta
Originally published on Towards AI.
Keswani’s Algorithm introduces a novel approach to solving two-player non-convex min-max optimization problems, particularly in differentiable sequential games where the sequence of player actions is crucial. This blog explores how Keswani’s method addresses common challenges in min-max scenarios, with applications in areas of modern Machine Learning such as GANs, adversarial training, and distributed computing, providing a robust alternative to traditional algorithms like Gradient Descent Ascent (GDA).
Problem Setting:
We consider differentiable sequential games with two players: a leader who can commit to an action, and a follower who responds after observing the leader’s action. Particularly, we focus on the zero-sum case of this
problem which is also known as minimax optimization, i.e.,
![[AI/ML] Keswani’s Algorithm for 2-player Non-Convex Min-Max Optimization [AI/ML] Keswani’s Algorithm for 2-player Non-Convex Min-Max Optimization](https://miro.medium.com/v2/resize:fit:700/1*gtYIsACNBX9EvoDj3RyXkw.png)
Unlike simultaneous games, many practical machine learning algorithms, including generative adversarial net-works (GANs) [2] [3] , adversarial training [4] and primal-dual reinforcement learning [5], explicitly specify theorder of moves between players and the order of which player acts first is crucial for the problem. In particular, min-max optimisation is curcial for GANs [2], statistics, online learning [6], deep learning, and distributed computing [7].

Therefore, the classical notion of local Nash equilibrium from simultaneous games may not be a proper definition of local optima for sequential games since minimax is in general not equal to maximin. Instead, we consider the notion of local minimax [8] which takes into account the sequential structure of minimax optimization.
Models and Methods:
The vanilla algorithm for solving sequential minimax optimization is gradient descent-ascent (GDA), where both players take a gradient update simultaneously. However, GDA is known to suffer from two drawbacks.
- It has undesirable convergence properties: it fails to converge to some local minimax and can converge to fixed points that are not local minimax [9] [10]
- GDA exhibits strong rotation around fixed points, which requires using very small learning rates[11] [12] to
converge.
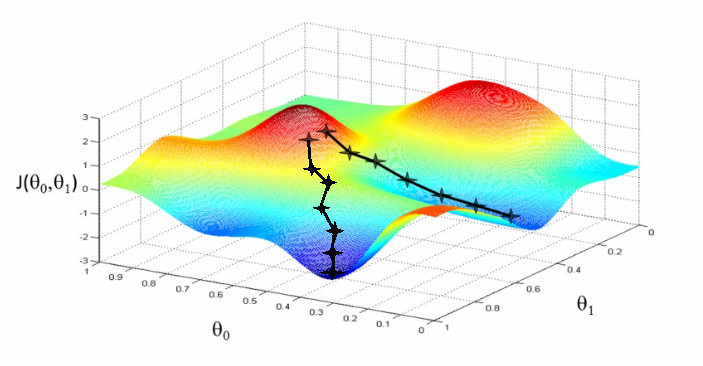
Recently, there has been a deep interest in min-max problems, due to [9] and other subsequent works. Jin et al. [8] actually provide great insights to the work.
Keswani’s Algorithm:
The algorithm essentially makes response function : max
y∈{R^m} f (., y) tractable by selecting y-updates (maxplayer) in
greedy manner by restricting selection of updated (x,y) to points along sets P(x,y) (which is defined as set of endpoints of paths such that f(x,.) is non-decreasing). There are 2 new things that this algorithm does to make
computation feasible:
- Replace P(x, y) with Pε (x, y) (endpoints of paths along which f(x,.) increases at some rate ε > 0 (which makes
updates to y by any ’greedy’ algorithm (as Algorithm 2) feasible) - Introduce a ’soft’ probabilistic condition to account for discontinuous functions.

Experimental Efficacy:
A Study [16] done at EPFL (by Shashwat et al., ) confirmed the efficacy of Keswani’s Algorithm in addressing key limitations of traditional methods like GDA (Gradient Descent Ascent) and OMD (Online Mirror Descent), especially in avoiding non-convergent cycling. The study proposed following future research avenues:
- Explore stricter bounds for improved efficiency.
- Incorporate broader function categories to generalize findings.
- Test alternative optimizers to refine the algorithm’s robustness.
The full study for different functions is as follows:
Keswani's Algorithm for non-convex 2 player min-max optimisation
Keswani's Algorithm for non-convex 2 player min-max optimisation –
www.slideshare.net
References:
[1] V. Keswani, O. Mangoubi, S. Sachdeva, and N. K. Vishnoi, “A convergent and dimension-independent first-order algorithm for min-max
optimization,” arXiv preprint arXiv:2006.12376, 2020.
[2] I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, and Y. Bengio, “Generative adversarial
networks,” Communications of the ACM, vol. 63, no. 11, pp. 139–144, 2020.
[3] M. Arjovsky, S. Chintala, and L. Bottou, “Wasserstein generative adversarial networks,” pp. 214–223, 2017.
[4] A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu, “Towards deep learning models resistant to adversarial attacks,” arXiv
preprint arXiv:1706.06083, 2017.
[5] W. S. Cho and M. Wang, “Deep primal-dual reinforcement learning: Accelerating actor-critic using bellman duality,” arXiv preprint
arXiv:1712.02467, 2017.
[6] N. Cesa-Bianchi and G. Lugosi, Prediction, Learning, and Games. Cambridge University Press, 2006.
[7] J. Shamma, Cooperative Control of Distributed Multi-Agent Systems. Wiley & Sons, Incorporated, John, 2008.
[8] C. Jin, P. Netrapalli, and M. Jordan, “What is local optimality in nonconvex-nonconcave minimax optimization?” pp. 4880–4889, 2020.
[9] Y. Wang, G. Zhang, and J. Ba, “On solving minimax optimization locally: A follow-the-ridge approach,” arXiv preprint arXiv:1910.07512,
2019.
[10] C. Daskalakis and I. Panageas, “The limit points of (optimistic) gradient descent in min-max optimization,” Advances in neural information
processing systems, vol. 31, 2018.
[11] L. Mescheder, S. Nowozin, and A. Geiger, “The numerics of gans,” Advances in neural information processing systems, vol. 30, 2017.
[12] D. Balduzzi, S. Racaniere, J. Martens, J. Foerster, K. Tuyls, and T. Graepel, “The mechanics of n-player differentiable games,” pp. 354–363,
2018.
[13] D. M. Ostrovskii, B. Barazandeh, and M. Razaviyayn, “Nonconvex-nonconcave min-max optimization with a small maximization domain,”
arXiv preprint arXiv:2110.03950, 2021.
[14] J. Yang, N. Kiyavash, and N. He, “Global convergence and variance reduction for a class of nonconvex-nonconcave minimax problems,”
Advances in Neural Information Processing Systems, vol. 33, pp. 1153–1165, 2020.
[15] G. Zhang, Y. Wang, L. Lessard, and R. B. Grosse, “Near-optimal local convergence of alternating gradient descent-ascent for minimax
optimization,” pp. 7659–7679, 2022.
[16] S. Gupta, S. Breguel, M. Jaggi, N. Flammarion “Non-convex min-max optimisation”, https://vixra.org/pdf/2312.0151v1.pdf
Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI














