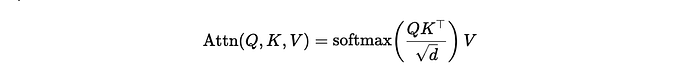
Non-Linear Models

Last Updated on August 2, 2022 by Editorial Team

Author(s): Dr. Marc Jacobs

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

When the formula looks nice but is hurting the analysis

This is not my first blog concerning non-linear models. In fact, if you sift through my lists of blogs, you can see I applied quite a couple of them. Personally, I like non-linear models since they have a biological basis, and if you have data that does not connect to that basis, it can become quite a challenge to move further. As always, the first steps are the hardest, and nothing suits that premise better than a non-linear model.

I will not dive into a talk about non-linear models, but what I will do is show you briefly my struggle with a dataset handed to me by another researcher. This is nutritional commercial data, so I cannot share the data itself, but you can see what I did. Also, the formula given to me is beyond my comprehension, but what I will show is that a perfect-looking formula can be quite difficult to work with if it fits the data too perfectly.

Let's start by loading the libraries and the data. It is data coming from piglets, measured across time.

rm(list = ls())
library(readr)
library(nlstools)
library(nlme)
library(ggplot2)
library(nls2)

## new file from Theo
Oral_data_for_Marc <- read_delim("Oral data for Marc.csv", 
                                 ";", escape_double = FALSE, trim_ws = TRUE)
data<-Oral_data_for_Marc
rm(Oral_data_for_Marc)
data<-data[, 1:3]
data<-data[complete.cases(data),]
head(data);str(data)
as.numeric(gsub(",", ".", gsub("\\.", "", data$D9std)))
data$D9std <- gsub(",", "", data$D9std)
data$D9std <- as.numeric(data$D9std)                          
data$D9std<-data$D9std/1000000000
data$Big<-as.factor(data$Big)

The data for each piglet (**Big**), time, and the outcome of interest.

Now, the data was not easy to work with from the start, especially the outcome. It was loaded as a character, but I could not make a numeric on the spot, forcing me to do some transformations first.

ggplot(data, 
       aes(x=time, 
           y=D9std, 
           group=Big, 
           col=Big))+
  geom_point()+
  geom_line()+
  theme_bw()+
  labs(x="Time", 
       y="Value", 
       col="Pig" )

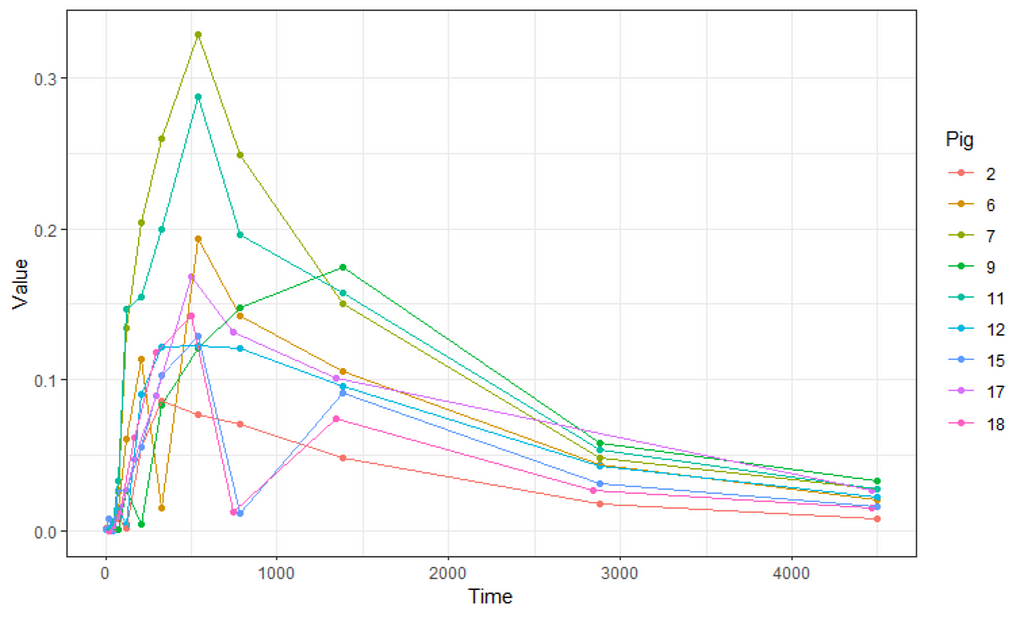
Plotting the data. I have nine piglets, showing data across time (seconds). The majority follow a distinct pattern, but not all, and this will cause our non-linear model some trouble.

Not only will the pathway cause issues, but also the beginning, which is why I cut a couple of seconds from the data. Let's see how the data will look then.

datasub<-data[data$time>=30,];head(datasub)
colnames(datasub)[2]<-"x" # time called x
colnames(datasub)[3]<-"y" # D9std called y
datasub$Big<-NULL # not informative vector
datasub<-as.data.frame(datasub)
datasub$y <- gsub(",", "", datasub$y)                          
datasub$y<-as.numeric(datasub$y)
head(data)
head(datasub);str(datasub)
plot(datasub$x, datasub$y)

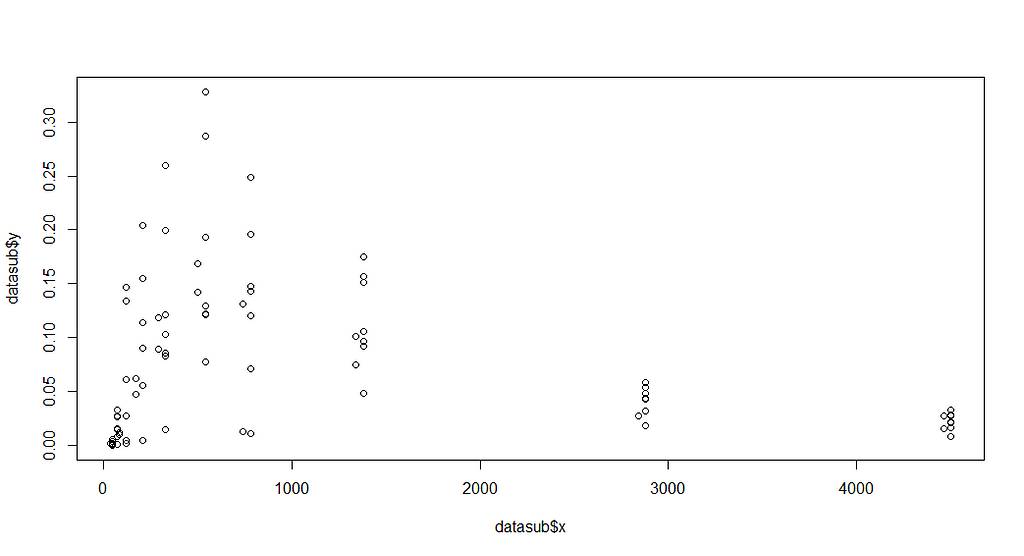
Now, it is time to look at the formula. As I said, this was handed to me, and I have no idea how somebody ever came up with such an elaborate formula. It truly is massive, with several compartments included. Below you see ways to connect the formula and how I test it to make sure I translated it correctly in R.

formulaExp<-as.formula(y~P*(I(1-(exp(-(Ks*x))))^B)*(Ka*((exp(-(Ke*x)))-(exp(-(Ka*x))))/(Ka-Ke)))

f1<-function(x, P, Ks,B, Ka, Ke){
  P*(I(1-(exp(-(Ks*x))))^B)*(Ka*((exp(-(Ke*x)))-(exp(-(Ka*x))))/(Ka-Ke))}

f1(20, P=2.48, Ks=0.014, B=1.52, Ka=0.00059, Ke=0.00690)

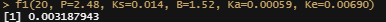
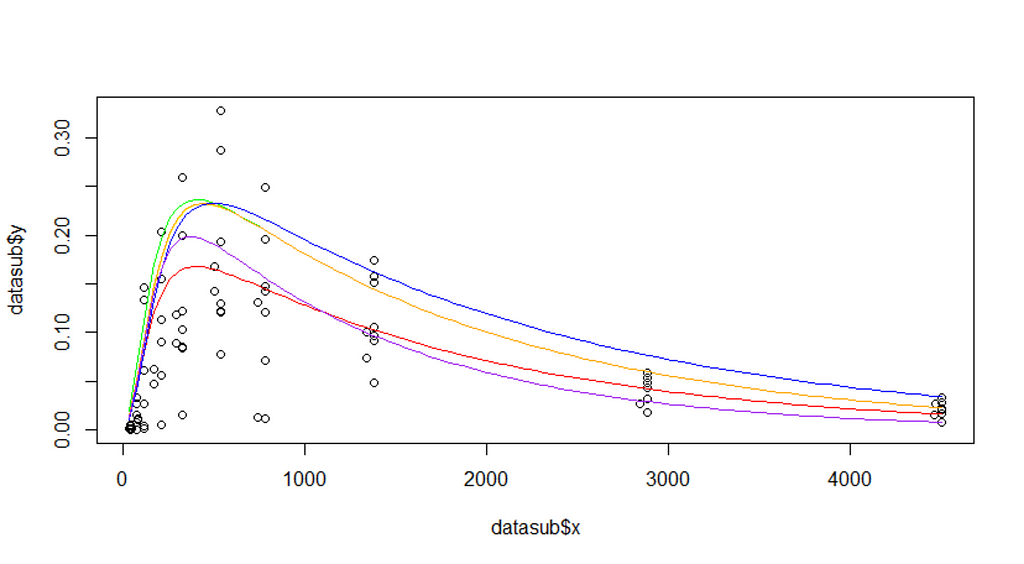
The biggest hurdle in non-linear regression modeling is finding the exact values. Since non-linear models are not closed, the search goes iterative. One way of taking a peak is by plotting the data and overlaying several gradations of the curve.

plot(datasub$x, datasub$y)
curve(f1(x, P=2.48, Ks=0.014, B=1.52, Ka=0.00059, Ke=0.00690), add=T, col="red") 
curve(f1(x, P=3.5, Ks=0.014, B=1.52, Ka=0.00059, Ke=0.00690), add=T, col="green") 
curve(f1(x, P=3.5, Ks=0.010, B=1.52, Ka=0.00059, Ke=0.00690), add=T, col="yellow") 
curve(f1(x, P=3.5, Ks=0.010, B=1.52, Ka=0.00050, Ke=0.00590), add=T, col="blue") 
curve(f1(x, P=3.5, Ks=0.010, B=1.42, Ka=0.00059, Ke=0.00690), add=T, col="orange") 
curve(f1(x, P=3.0, Ks=0.010, B=1.62, Ka=0.00080, Ke=0.0090), add=T, col="purple")

This actually looks very, very nice! The curves follow the data in a splendid fashion. The formula IS quite complex, though but it works wonders.

A simple way of checking if the coefficients for each of the parameters, as chosen, come close to the average value seen in the data. This exercise was an additional check but not really necessary anymore considering the curves fitted above.

In R, there is a very nice package called NLStools, which will help you look at the data and offer functions to preview the coefficients you deem to be a good fit. Like I said before, that process is quite difficult, and unlike simple linear regression or mixed modeling, decent starting values are key in finding the solution. If there is one.

Residual Sums of Squares are provided which does not mean that much without comparison. However, considering the scale, it is still more than you would like.

The picture that belongs to the preview process. The model looks good, but the high Residual Sum of Squares is to be explained for sure.

Up until now, I have fed the formula a single or just a couple of scenarios. That is good if you know where to look but often you do not, so it is better to conduct a grid search. What this simply means is that you create a matrix of combinations and then let the model sift to that.

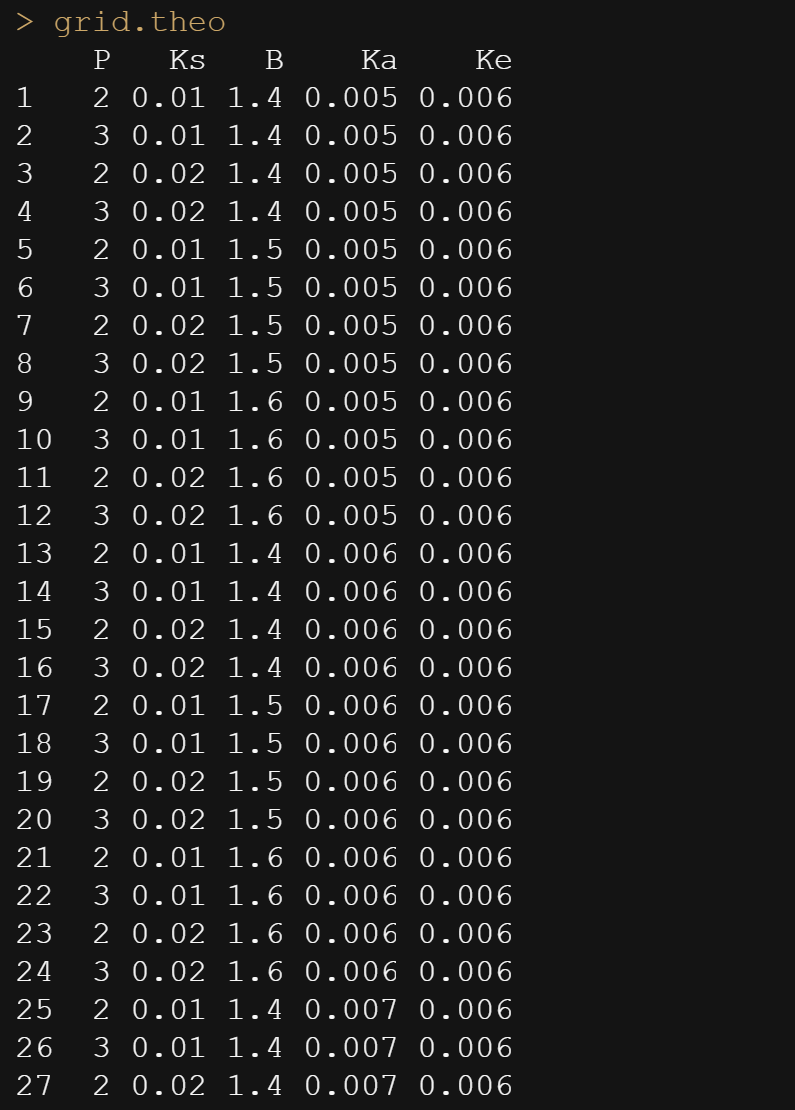
Below is the command for the grid and how it looks.

grid.theo<-expand.grid(list(P=seq(2, 4, by=0.1), 
                            Ks=seq(0.010, 0.020, by=0.01), 
                            B=seq(1.4, 1.6, by=0.01), 
                            Ka=seq(0.005,0.007,by=0.01),
                            Ke=seq(0.006,0.008, by=0.01))) 
grid.theo

Then, it is time to feed the model the grid.

mod1 <- nls2(formulaExp,
             data=datasub,
             start = grid.theo, 
             algorithm = "brute-force")
plot(mod1)
nls2(formulaExp, data=datasub, start = mod1)

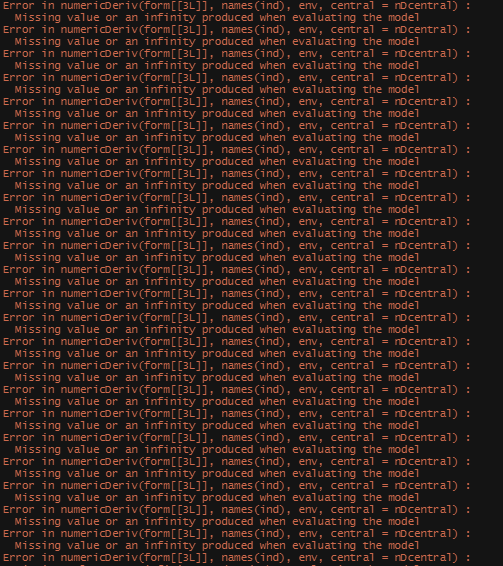
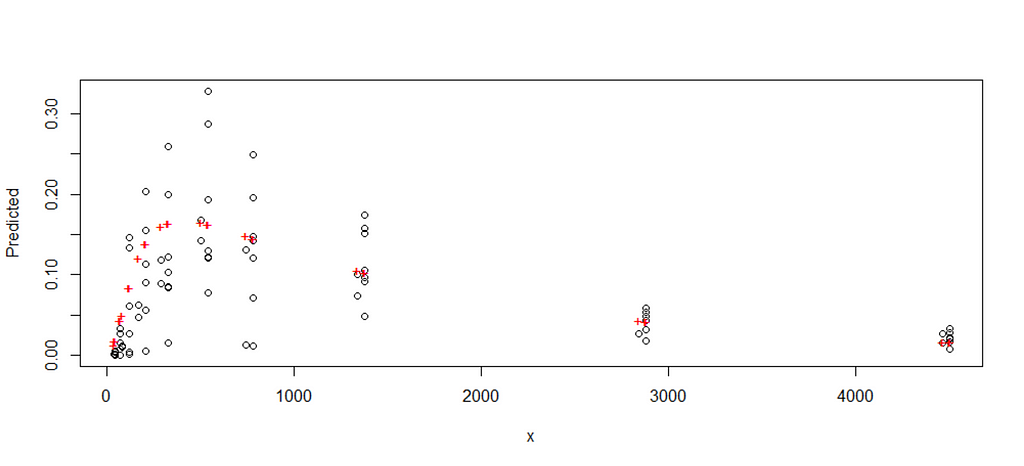
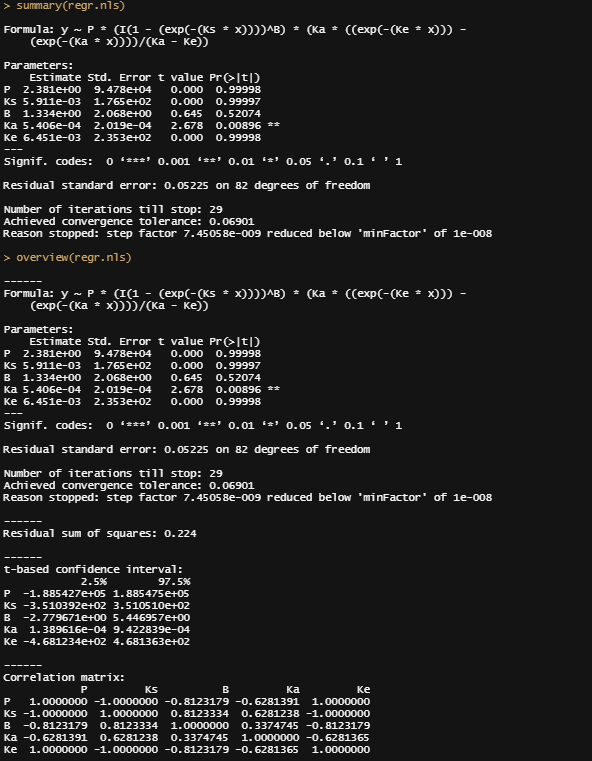
However, the model does produce. You can see the formula, the coefficients, and the residual sum of squares of the model chosen. It looks a lot higher than the value I obtained from the last preview.

Now, there ARE other ways of using grid searches by connecting them directly to the model. Here, you see me going at it again.

f1_nls_fit <- nls.multstart::nls_multstart(y ~ f1(x, P, Ks,B, Ka, Ke),data = datasub,
lower=c(P=2, Ks=0.01, B=1.4, Ka=0.005, Ke=0.006),
upper=c(P=4, Ks=0.02, B=1.6, Ka=0.007, Ke=0.008),
start_lower = c(P=2, Ks=0.01, B=1.4, Ka=0.005, Ke=0.006),
start_upper = c(P=4, Ks=0.02, B=1.6, Ka=0.007, Ke=0.008),
iter = 500,supp_errors = "Y")

summary(f1_nls_fit)
plot(f1_nls_fit)

plot_nls <- function(nls_object, data) {
  predframe <- tibble(x=seq(from=min(datasub$x), to=max(datasub$x), 
                               length.out = 1024)) %>%
    mutate(ypred = predict(nls_object, newdata = list(x=.$x)))
  ggplot(data, aes(x=x, y=y)) +
    geom_point(size=3, alpha=0.5) +
    geom_line(data = predframe, 
              aes(x=x, y=ypred), 
              col="red", lty=2)+
    theme_bw()}

plot_nls(f1_nls_fit, datasub)

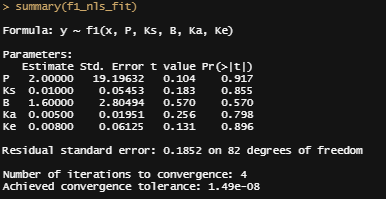
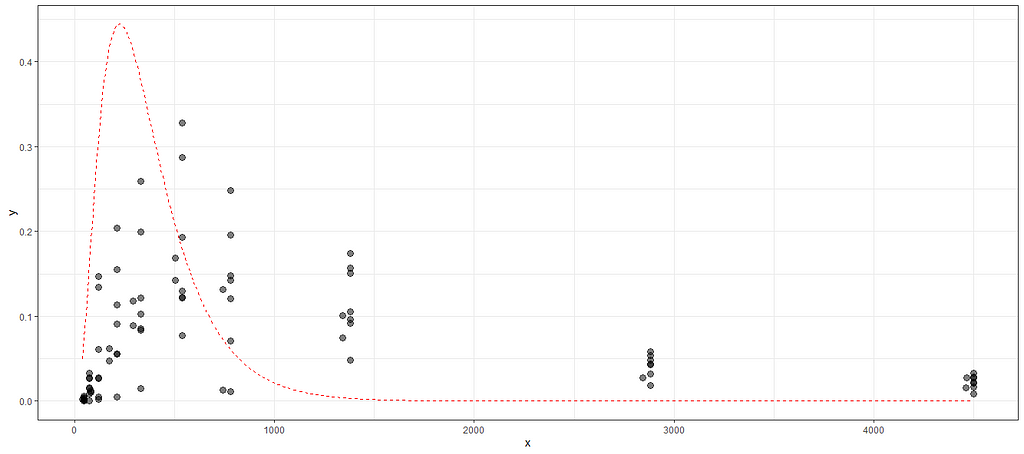
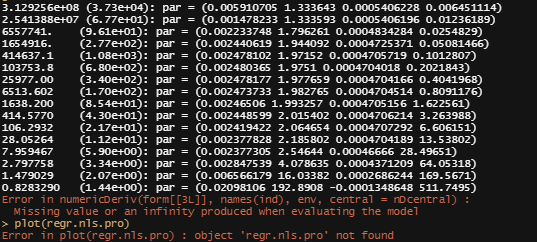
The residual standard error is way lower now, convergence is acquired easily, and we have decent coefficients. But then, I start looking at the standard errors, and I get worried.

This is NOT what you want to see for obvious reasons.

Let's try again, changing the control measures and from a single list of starting coefficients.

control1<-nls.control(maxiter=100, tol=1e-10, minFactor=1/100000000, warnOnly=T)

regr.nls<-nls(formulaExp,start=list(P=2.48, Ks=0.014, B=1.52, Ka=0.00059, Ke=0.00690),control=control1, data=datasub, trace=T)

summary(regr.nls)
overview(regr.nls)
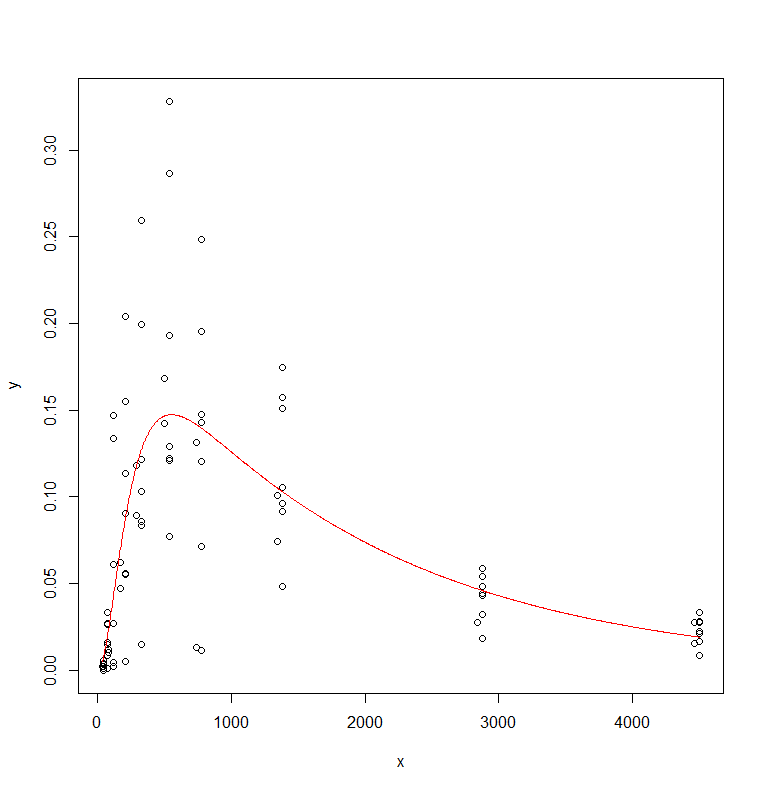
plotfit(regr.nls, smooth=T)

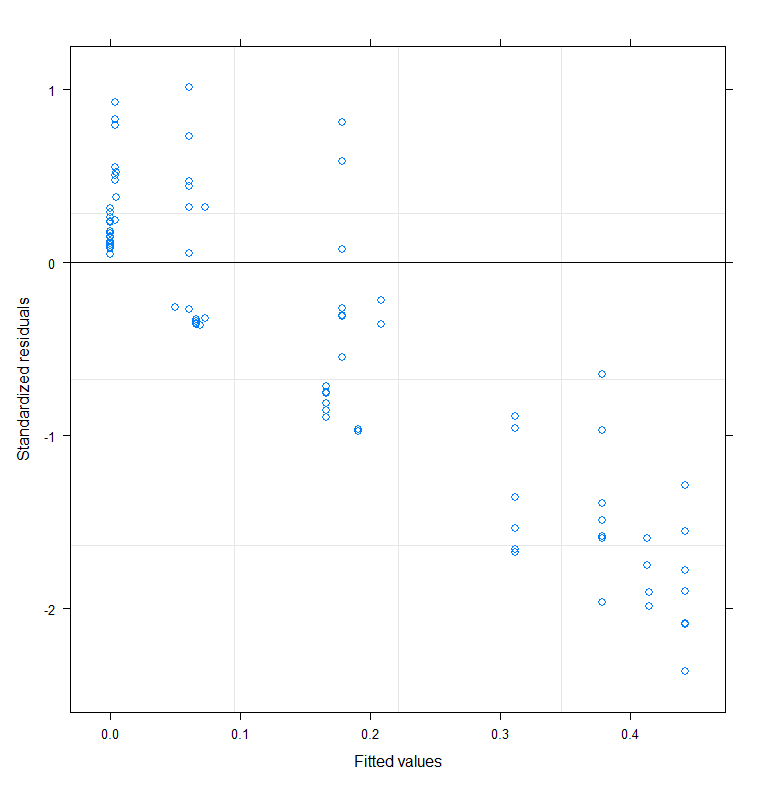
Not much better. In fact, THIS overview reveals the issue at hand. The standard errors are so big because the parameters in the model are near-identical. They correlate perfectly, which makes them redundant and the model unstable. This is NOT what you want and what looked like a perfect well-crafted non-linear formula now becomes a problem.

Even though the mean values look very nice.

Let's take a closer look at the residuals.

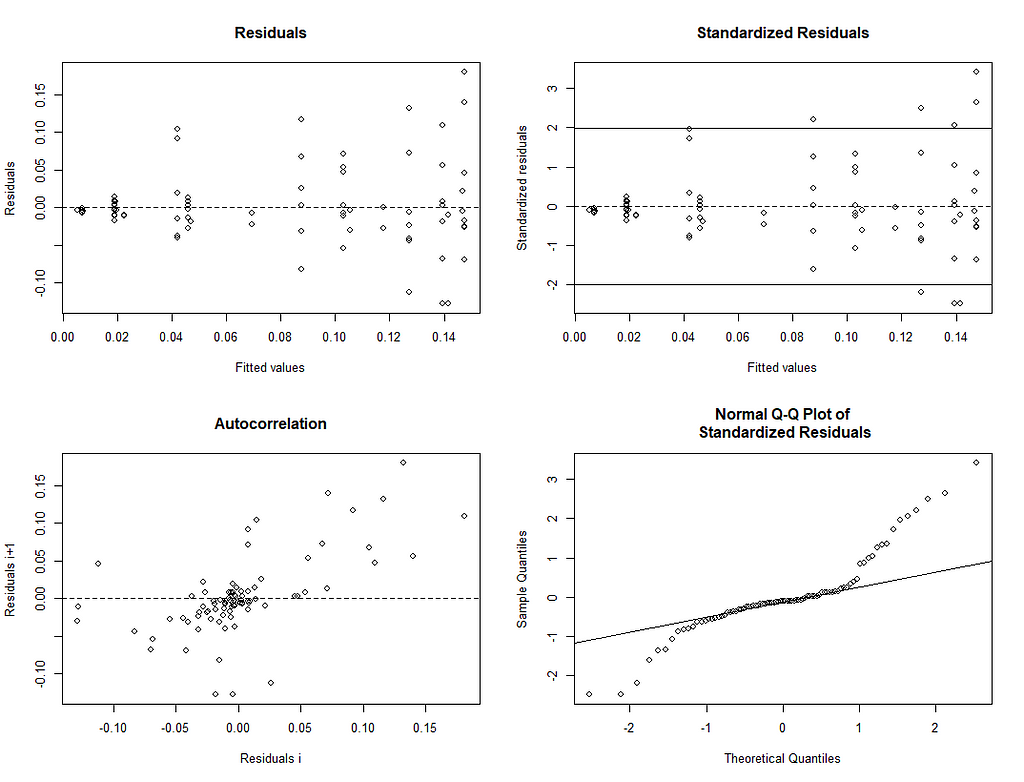
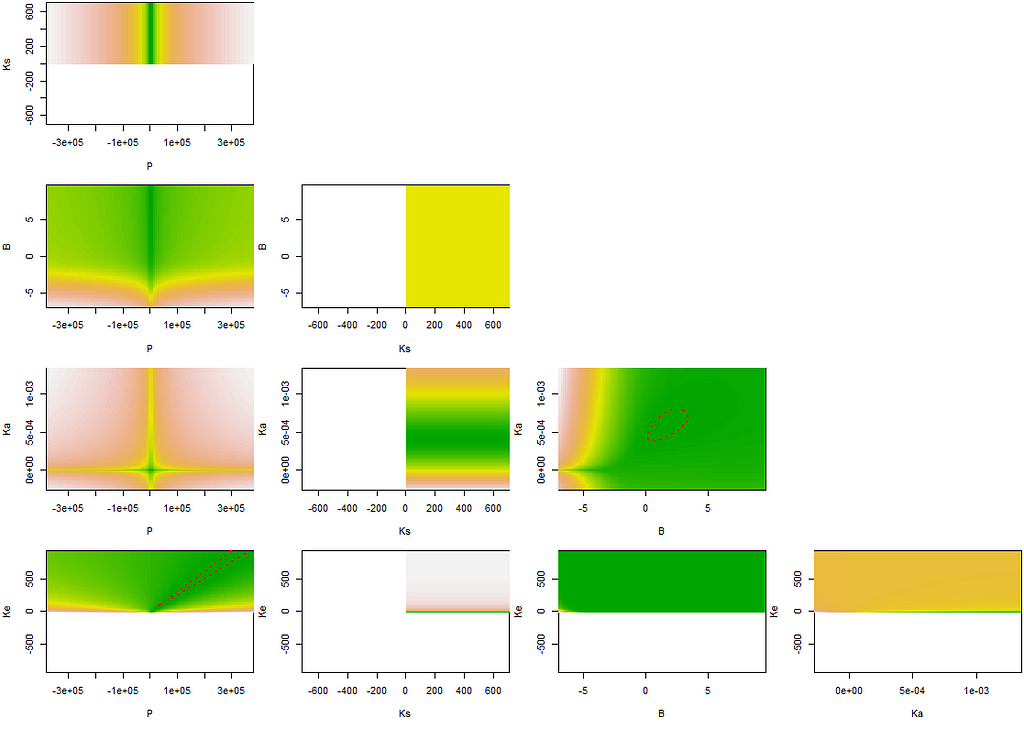
Not bad, but also not very good. Even if it were good, I would not have kept the formula since a perfect correlation between coefficients (multicollinearity) is really something you need to try and avoid!

A more decent way of showing the interconnectedness of the coefficients is to plot contours.

regr.cont1<-nlsContourRSS(regr.nls) 
plot(regr.cont1)
regr.conf1<-nlsConfRegions(regr.nls,exp=4, length=20) 
plot(regr.conf1, bound=T)
regr.nls.pro<-profile(regr.nls)
plot(regr.nls.pro)

For some, like everything with P, it was not even possible. For the ones that are possible, I do not really know what to make of it. It does not look decent, it does not feel decent and it does not operate decent.

And the functions are not liking what they see either.

This is not working out. If I want to take a look at the data, I need to do more.

Perhaps, it is time to look at the mixed modeling side of non-linear regression. We have multiple pigs, so it should be possible and those of you who remember the first plots also remember that not every pig had the same curve.

I will turn to the nlme package, which I have relied heavily on one before, and start grouping the data in a dataset that nlme likes.

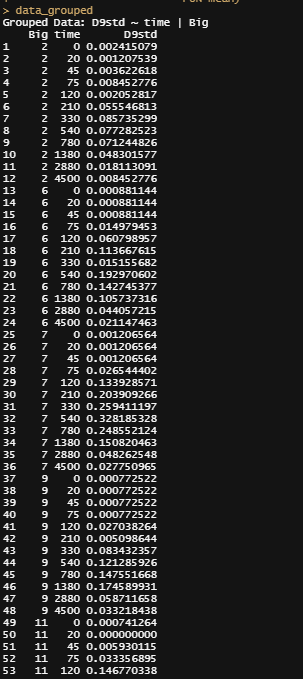
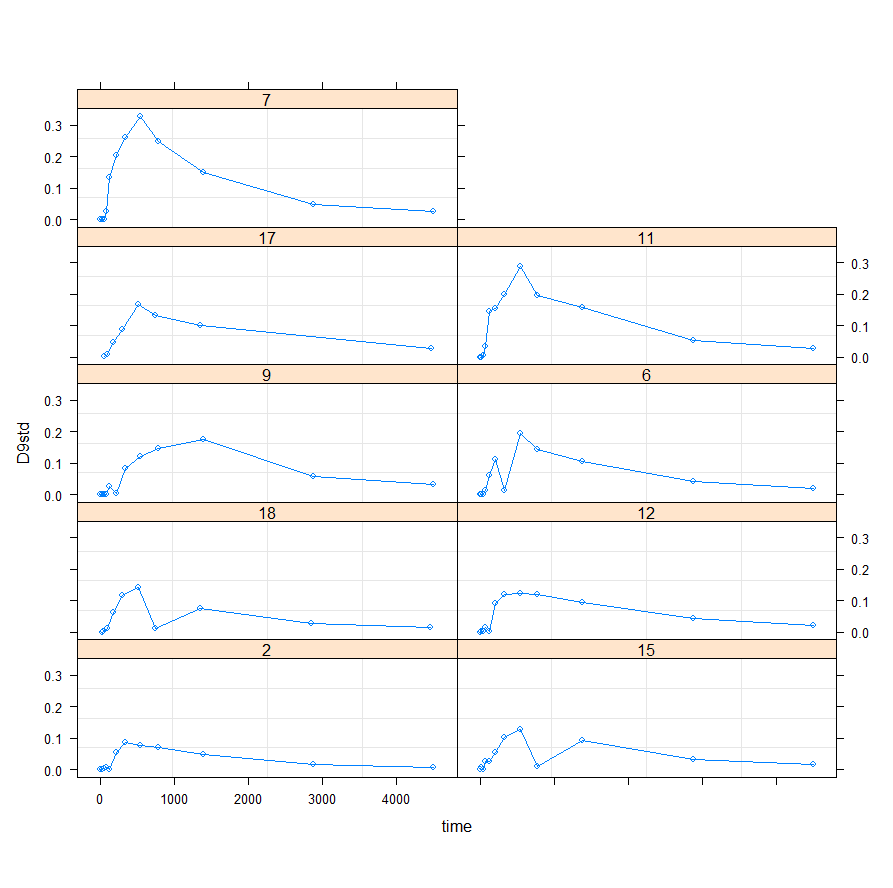
Grouped data in a table and plotted. For sure, not every pig has the same curve. This is where non-linear models struggle, since they have a particular freedom in the box. And I am getting the feeling their box is much smaller than what the data requires.

Lets go for it!

f1_nlme_fit <- nlme(D9std ~ f1(time, P, Ks, B, Ka, Ke),
                    data = data_grouped, 
                    fixed = P + Ks + B + Ka + Ke ~ 1, 
                    random = P ~ 1, 
                    groups = ~ Big, 
                    start = c(P=2.48, Ks=0.014, B=1.52, Ka=0.00059,  
                    Ke=0.00690),verbose = F)

This brings me back to the original overview some time back, showing me the heavy correlations. This will just never work, the formula is too stringent! And since I have no idea how it was made up, I decided to go for a different model altogether. One that would offer me more freedom at the expense of biological explainability.

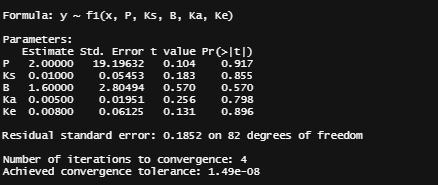
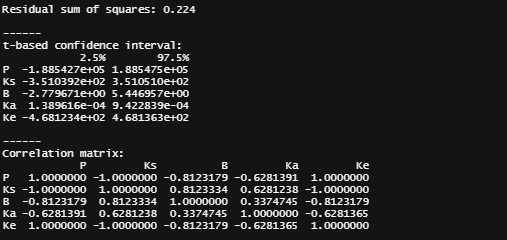
General Additive Mixed Models — using time as a spline and still keeping the grouped dataset. However, without specifying the hierarchy specified in the model, nothing will happen.

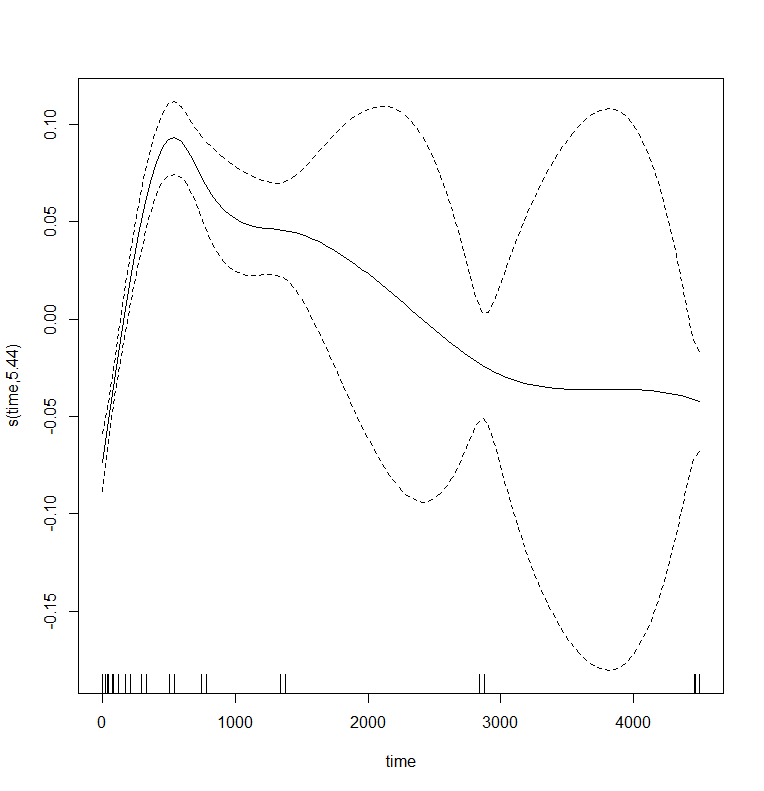
gamm_fit<-mgcv::gamm(D9std~s(time), data=data_grouped)
plot(gamm_fit$gam,pages=1)
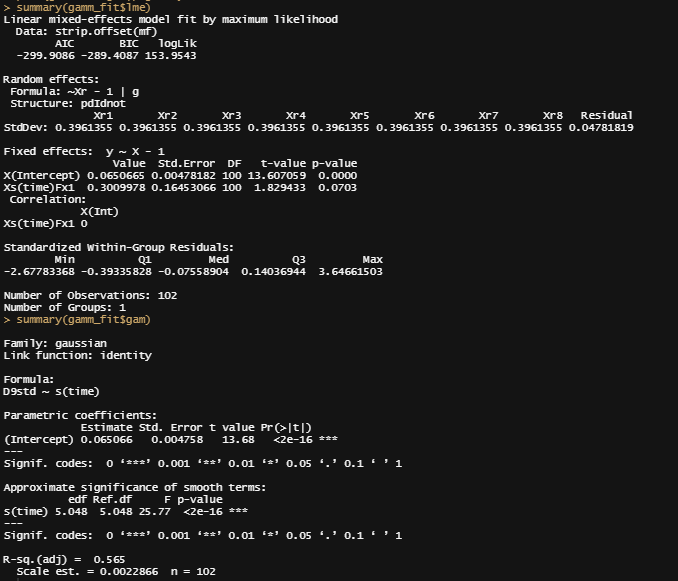
summary(gamm_fit$lme) 
summary(gamm_fit$gam) 
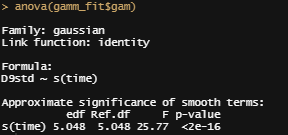
anova(gamm_fit$gam) 
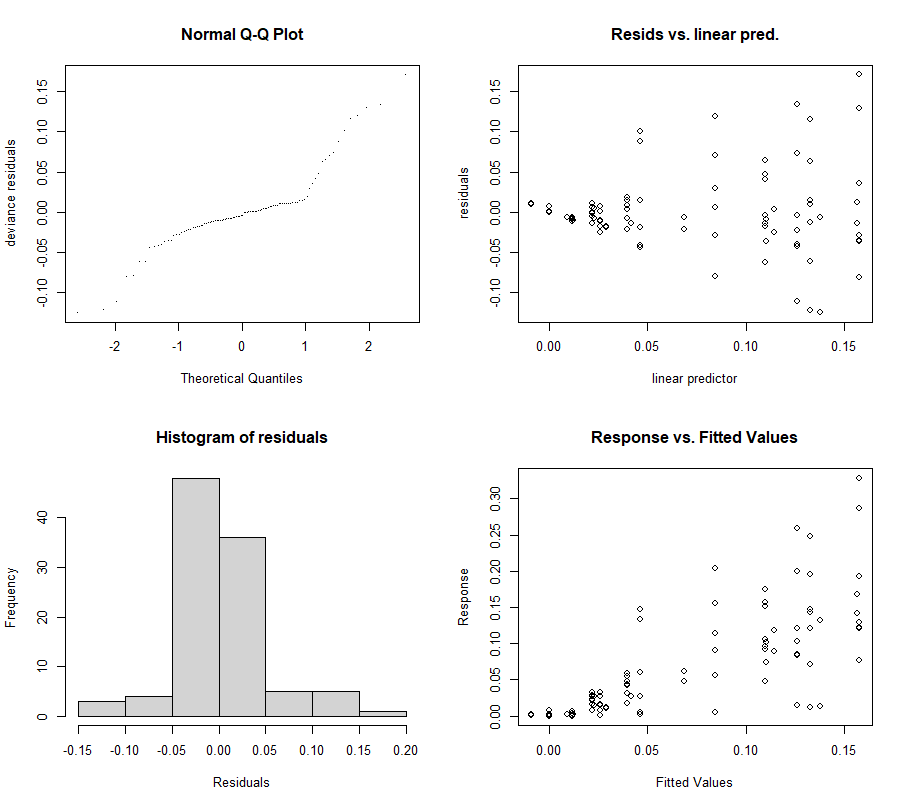
par(mfrow = c(2, 2))
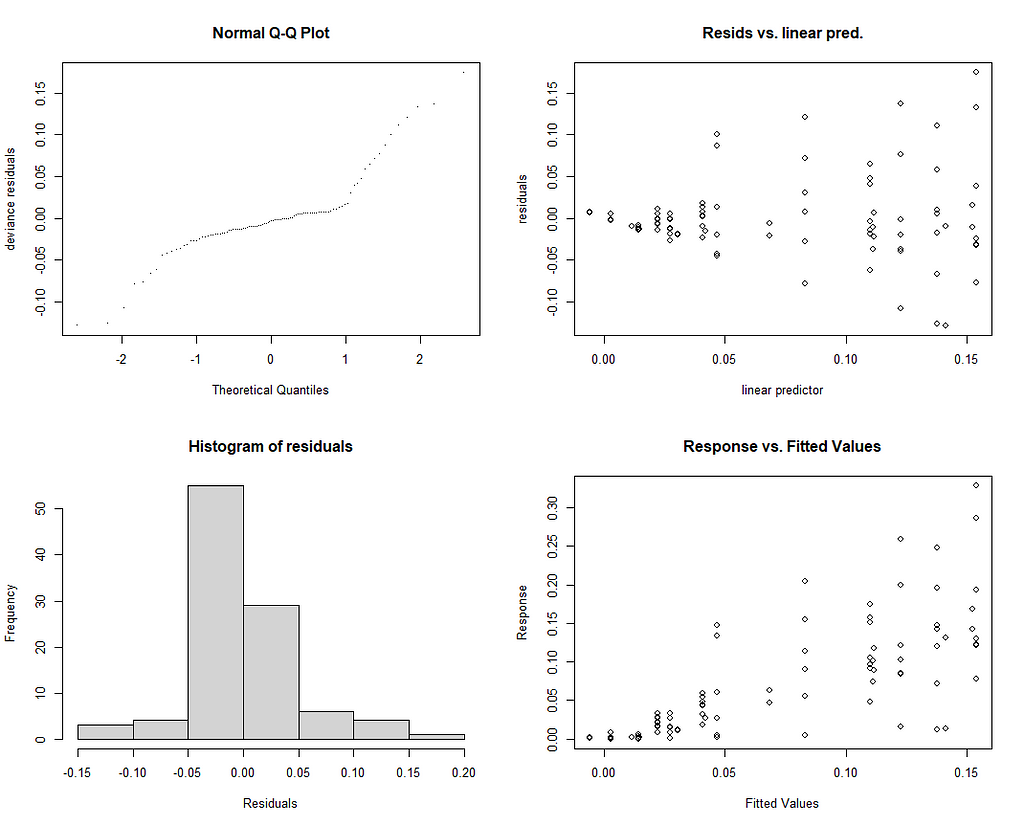
mgcv::gam.check(gamm_fit$gam)

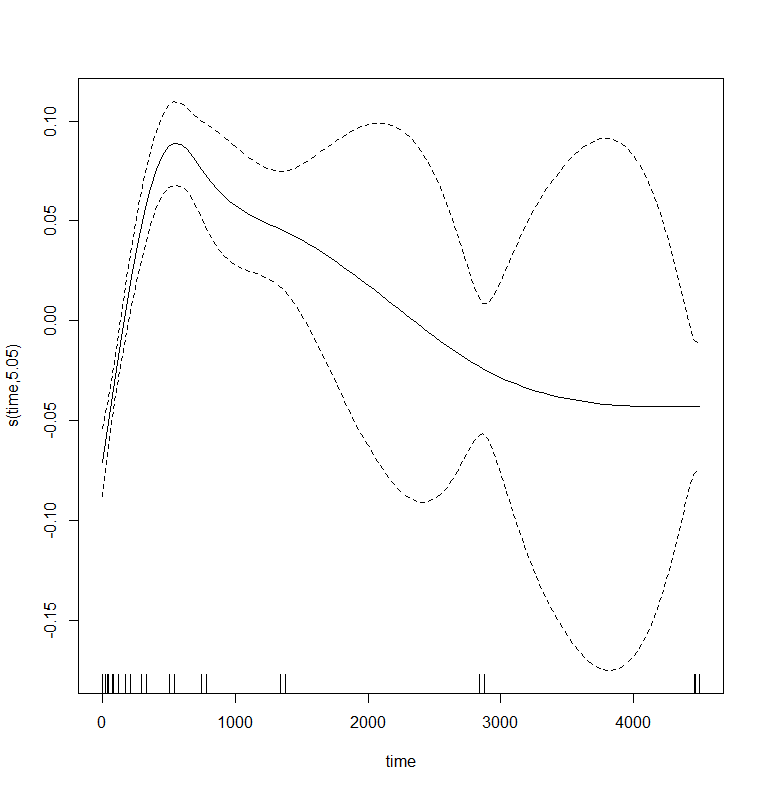
The mean curve looks good but the confidence bands are FUNKY. Welcome to the consequence of having high variance and some weird curves in the data.

And the lme (mixed model) part of the gamm function.

Residuals show clearly how the model is losing its grip on the data. Too much variance, too much spread to be of much use.

Let's incorporate the hierarchy in the model by adding a random intercept.

gamm_fit2<-mgcv::gamm(D9std~s(time),
                      data=data_grouped,
                      random=list(Big=~1))
plot(gamm_fit2$gam,pages=1)
big <- data_grouped$Big
rm(big)
par(mfrow = c(2, 2))
mgcv::gam.check(gamm_fit2$gam)

Nothing really changed to be honest. To be expected, the variance was not really at the start.

Let's add a random slope as well.

gamm_fit2.1<-mgcv::gamm(D9std~s(time),
                      data=data_grouped,
                      random=list(Big=~time))
anova(gamm_fit$lme, gamm_fit2$lme, gamm_fit2.1$lme)

Now, surprise surpise, it does not seam that the random slope is that much better. In fact, the random intercept does outperform the mean model, byt the random slope doe not. So, in line with wanting to have a **parsimonious** model, we will go with the AIC / Likelihood Ratio choice.

Last but not least, I want to check if the model I made makes any sense. Overfitting is always a problem, and since I have lost the biological relevance of the non-linear function, I want to make at least sure that this data-driven model is looking at the right things.

pred<-fitted(gamm_fit2$lme);pred
pred<-fitted(gamm_fit2$gam);pred

data_grouped$pred<-pred
ggplot(data_grouped, 
       aes(x=time))+
  geom_point(aes(y=D9std))+
  geom_point(aes(y=pred), col="red")+
  geom_line(aes(y=pred), col="red", lty=2)+
  theme_bw()+
  facet_wrap(~Big)

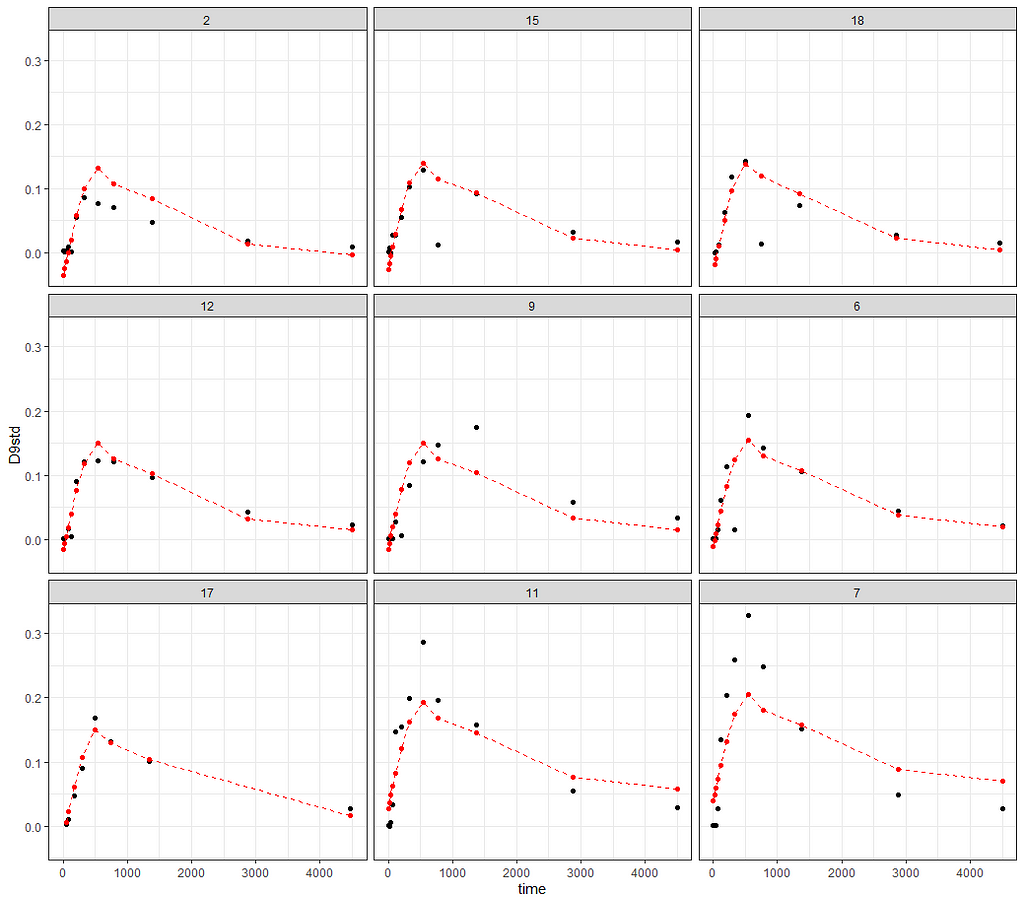
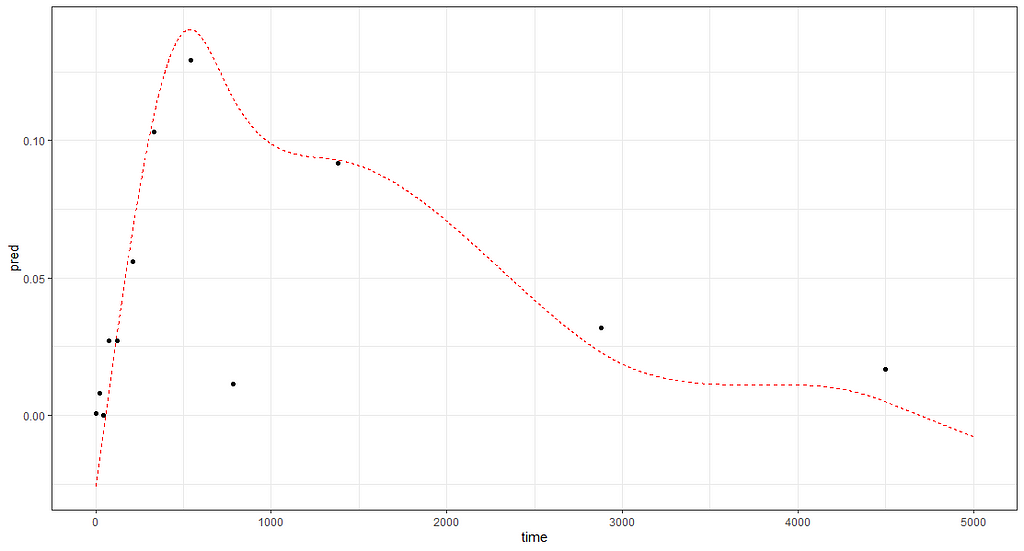
Looks like it does! For sure, the curves are different per pig and it does seem that the curves are following the data, to some degree. Nevertheless, with such a dataset, and such variance, only **time** will not do.

And the last check by creating a full time-path for a particular pig.

df<-data.frame(time = seq(0,5000, 1),Big  = "15")
rand_big<-ranef(gamm_fit2$lme, level=2)
df$pred<-rand_big$`(Intercept)`[2] + mgcv::predict.gam(gamm_fit2$gam,df)
ggplot(df, 
       aes(x=time))+
  geom_line(aes(y=pred), col="red", lty=2)+
  geom_point(data=data_grouped[data_grouped$Big=="15", ], 
             aes(x=time, y=D9std), col="black")+
    theme_bw()

So, I hope you liked this small post. Do not forget, modeling is not easy. That is why it is fun!

Non-Linear Models was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI

Frequently Used, Contextual References

Resources

Publication

Author(s): Dr. Marc Jacobs

When the formula looks nice but is hurting the analysis

Towards AI Team

Feedback ↓ Cancel reply

Popular posts

Best Laptops for Deep Learning, Machine Learning (ML), and Data Science for 2023

Best Workstations for Deep Learning, Data Science, and Machine Learning (ML) for 2022

Descriptive Statistics for Data-driven Decision Making with Python

Best Machine Learning (ML) Books - Free and Paid - Editorial Recommendations for 2022

Best Data Science Books - Free and Paid - Editorial Recommendations for 2022

Updates

Recent Posts

AI in Medical Imaging: A Life-Saving Revolution or Ethical Minefield?

AI in Medical Imaging: A Life-Saving Revolution or Ethical Minefield?

AI in Medical Imaging: A Life-Saving Revolution or Ethical Minefield?

AI in Medical Imaging: A Life-Saving Revolution or Ethical Minefield?

AI in Medical Imaging: A Life-Saving Revolution or Ethical Minefield?

The World’s Leading AI and Technology Publication.

Company

CONTACT US

Cookie	Duration	Description
cookielawinfo-checkbox-analytics	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Analytics".
cookielawinfo-checkbox-functional	11 months	The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional".
cookielawinfo-checkbox-necessary	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary".
cookielawinfo-checkbox-others	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Other.
cookielawinfo-checkbox-performance	11 months	This cookie is set by GDPR Cookie Consent plugin. The cookie is used to store the user consent for the cookies in the category "Performance".
viewed_cookie_policy	11 months	The cookie is set by the GDPR Cookie Consent plugin and is used to store whether or not user has consented to the use of cookies. It does not store any personal data.

Frequently Used, Contextual References

Resources

Publication

Non-Linear Models

Author(s): Dr. Marc Jacobs

When the formula looks nice but is hurting the analysis

Towards AI Team

Related posts

Feedback ↓ Cancel reply

Popular posts

Updates

Recent Posts

The World’s Leading AI and Technology Publication.

Company

CONTACT US

GDPR CCPA Statement