Regression Feature Selection using the Kydavra LassoSelector

Last Updated on September 18, 2020 by Editorial Team

Author(s): Vasile Păpăluță

Machine Learning

We all know the Occam’s Razor:

From a set of solutions took the one that is the simplest.

This principle is applied in the regularization of the linear models in Machine Learning. L1-regularisation (also known as LASSO) tend to shrink wights of the linear model to 0 while L2-regularisation (known as Ridge) tend to keep overall complexity as simple as possible, by minimizing the norm of vector weights of the model. One of Kydavra’s selectors uses Lasso for selecting the best features. So let’s see how to apply it.

Using Kydavra LassoSelector.

If you still haven’t installed Kydavra just type the following in the following in the command line.

pip install kydavra

Next, we need to import the model, create the selector, and apply it to our data:

from kydavra import LassoSelector

selector = LassoSelector()

selected_cols = selector.select(df, ‘target’)

The select function takes as parameters the panda's data frame and the name of the target column. Also, it has a default parameter ‘cv’ (by default it is set to 5) it represents the number of folds used in cross-validation. The LassoSelector() takes the next parameters:

• alpha_start (float, default = 0) the starting value of alpha.
• alpha_finish (float, default = 2) the final value of alpha. These two parameters define the search space of the algorithm.
• n_alphas (int, default = 300) the number of alphas that will be tested during the search.
• extend_step (int, default=20) if the algorithm will deduce that the most optimal value of alpha is alpha_start or alpha_finish it will extend the search range with extend_step, in such a way being sure that it will not stick and will find finally the optimal value.
• power (int, default = 2) used in formula 10^-power, defines the maximal acceptable value to be taken as 0.

So the algorithm after finding the optimal value of alpha will just see which weights are higher than 10^-power.

Let’s take see an example:

To show its performance I chose the Avocado Prices dataset.

After a bit of cleaning and training it on the next features:

'Total Volume', '4046', '4225', '4770', 'Small Bags', 'Large Bags', 'XLarge Bags', 'type', 'year'

The LinearRegression has the mean absolute error equal to 0.2409683103736682.

When LassoSelector applied on this dataset it chooses the next features:

'type', 'year'

Using only these features we got an MAE = 0.24518692823037008

A quite good result (keep in mind, we are using only 2 features).

Note: Sometimes is recommended to apply the lasso on scaled data. In this case, applied to the data, the selector didn’t throw away any feature. You are invited to experiment and try with scaled and unscaled values.

Bonus.

This module also has a plotting function. After applying the select function you can see why the selector selected some features and others not. To plot just type:

selector.plot_process()

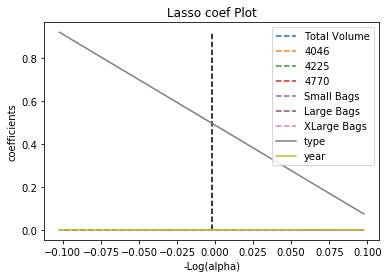
The dotted lines are features that were thrown away because their weights were too close to 0. The central-vertical dotted line is the optimal value of the alpha found by the algorithm.

The plot_process() function has the next parameters:

• eps (float, default = 5e-3) the length of the path.
• title (string, default = ‘Lasso coef Plot’) — the title of the plot.
• save (boolean, default= False) if set to true it will try to save the plot.
• file_path (string, default = None) if the save parameter was set to true it will save the plot using this path.

Conclusion

LassoSelector is a selector that usee the LASSO algorithm to select features the most useful features. Sometimes it will be useful to scale the features, we highly recommend you to try both.

If you tried kydavra we invite you to share your impression by filling out this form.

Made with ❤ by Sigmoid.

Useful links:

• https://en.wikipedia.org/wiki/Lasso_(statistics)
• https://towardsdatascience.com/feature-selection-using-regularisation-a3678b71e499

Regression Feature Selection using the Kydavra LassoSelector was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI