Logistic Regression with Mathematics

Last Updated on July 16, 2020 by Editorial Team

Author(s): Gul Ershad

Machine Learning, Mathematics

Introduction

Logistic Regression is an omnipresent and extensively used algorithm for classification. It is a classification model, very easy to use and its performance is superlative in linearly separable class. This is based on the probability for a sample to belong to a class. Here probabilities must be continuous and bounded between (0, 1). It is dependent on a threshold function to make a decision that is called Sigmoid or Logistic function.

To understand the concept of Logistic Regression, it is important to understand the concept of Odd Ration (OR), Logit function, Sigmoid function or Logistic function, and Cross-entropy or Log Loss.

Odds Ratio (OR)

Odds Ration (OR) is the odds in favor of a particular event. It is a measure of association between exposure and outcome.

Lets X is the probability of subjects affected and Yis a probability of subjects not affected, then, odds = X/Y

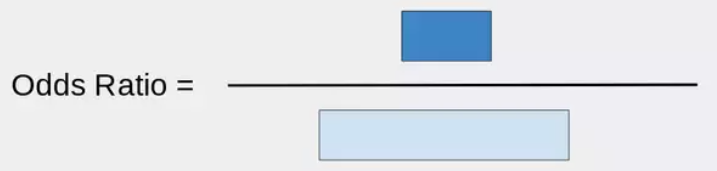
The formula of Odds Ratio:

Let’s take the probability range between 0 & 1. Let’s say…

Odds are the ratio of the probability of success and the probability of failure.

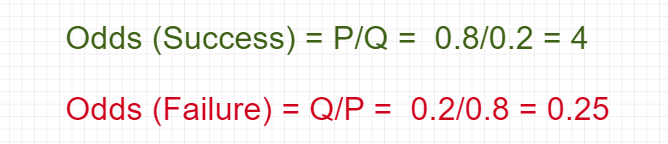
Problem Statement

Suppose that 7 out of 10 boys are admitted to Data Science while 3 of 10 girls are admitted. Find the probability of boys getting admitted to Data Science?

Solution

Lets P is the probability of getting admitted and Q is the probability of not getting admitted.

Probability of boys:

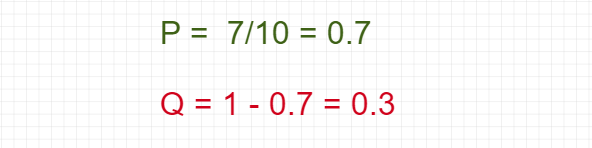
Probabilities of Girls:

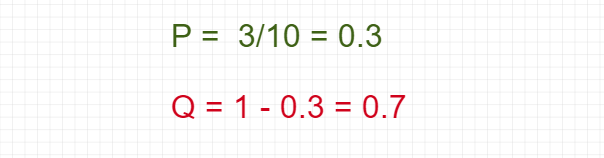
Now, calculate the odds of admission for both Boys and Girls:

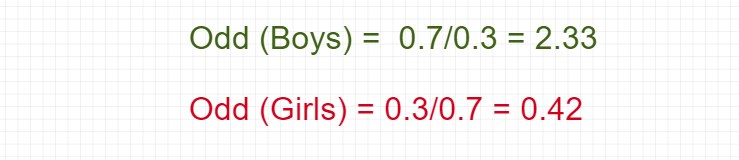
So, the Odds Ratio for getting admission in Data Science:

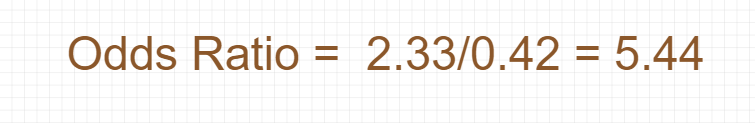
Conclusion: — for a boy the odd of being admitted are 5.44.

Logit Function

Logit function is the logarithm of the Odd Ratio (log-odds). It takes input values in the range 0 to 1 and then transforms them to value over the entire real number range.

Let’s take P as probability, then P/(1-P) is the corresponding odds; the logit of the probability is the logarithm of the odd given below:

Before the example of the logit function lets’ take the equation of Logistic Regression and relate with logit function to find probability:

Let’s take an example of a car whether the car will be sold or not?

So, equation:

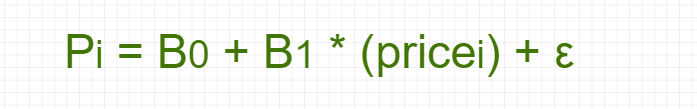
So,

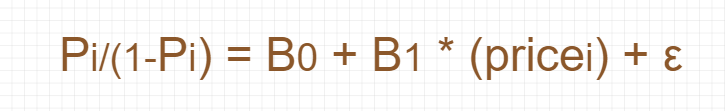
And, finally with a logit function

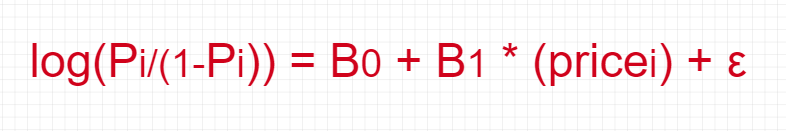
Problem Statement

Lets there is a car and its price is $ 45, 000 with an additional feature called a pink slip. Find the probability of sell for this car?

Solution

Lets’ write the equation of car will be sold or not?

Now, put the coefficient values as below:

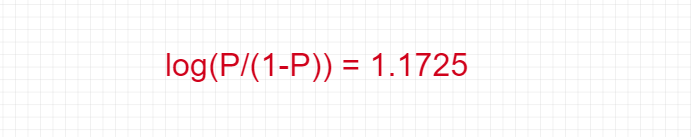
So,

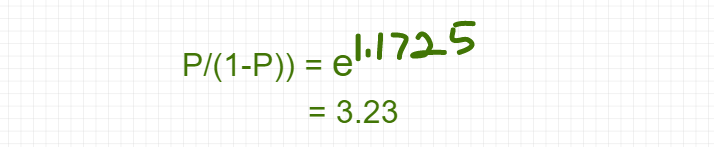
Hence,

Hence, the car has a probability of 76.4% chances of a sale.

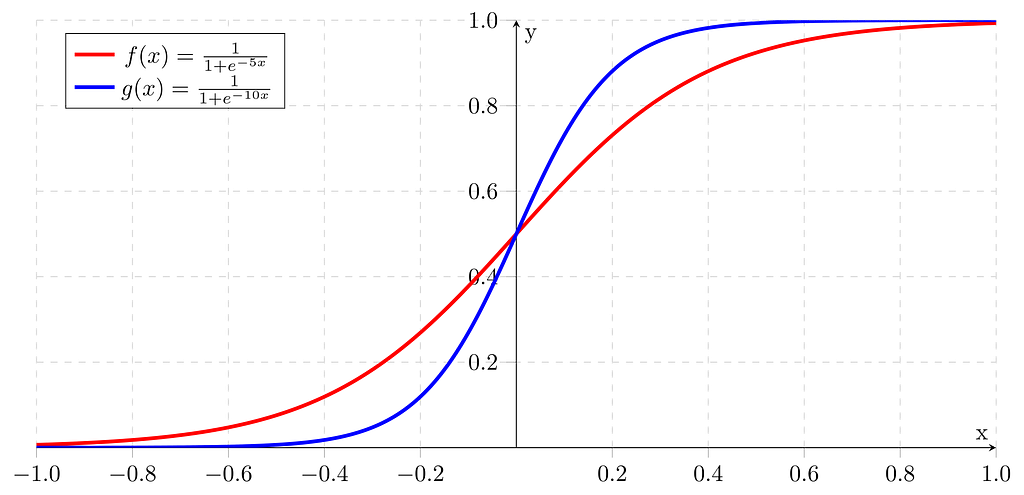
Logistic function or Sigmoid function

The inverse of the logit function is called the logistic function or Sigmoid function. It is named as Sigmoid function due to its characteristic shape.

The equation of the Sigmoid function ( from logit function):

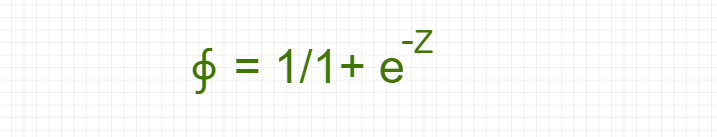
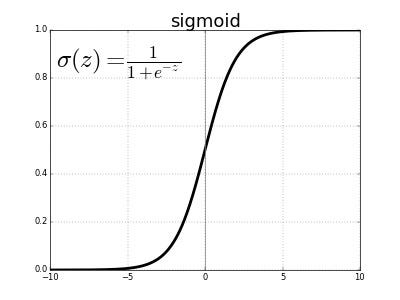
The sigmoid function takes real number values as input and transforms them into values in the range [0, 1] with an intercept ∮(Z) = 0.5.

Cross-Entropy or Log Loss

Cross-entropy is commonly used to quantify the difference between two probability distributions. This is used in Logistic Regression.

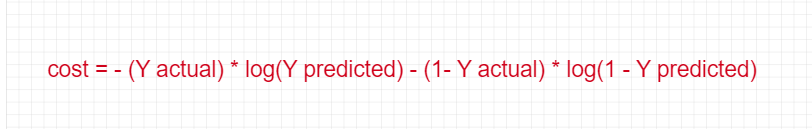
Or

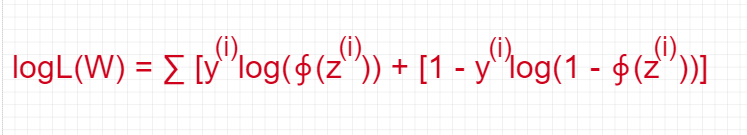
It is also called a log-likelihood function.

Conclusion

The base of Logistic Regression is dependent on different probabilistic equations like Odds Ration, Sigmoid function, etc. This classification model is very easy to implement and performs very well in linearly separable classes.

---

Logistic Regression with Mathematics was originally published in Towards AI — Multidisciplinary Science Journal on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI