How to Fit Large Language Models in Small Memory: Quantization

Author(s): Ivan Reznikov

Originally published on Towards AI.

The original article was published on my LinkedIn page.

Read more about LLMs in my Langchain 101 series:

Large Language Models

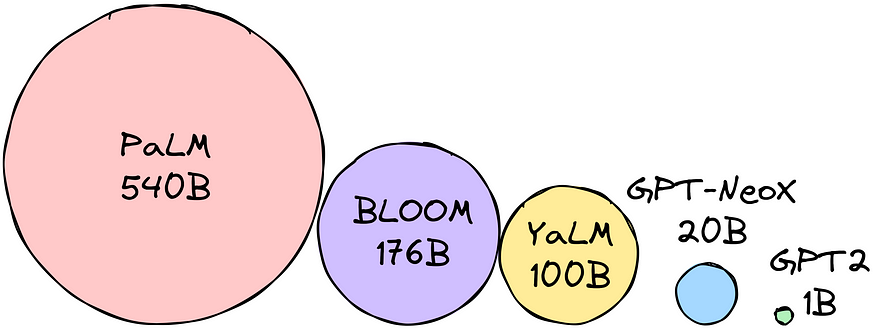
Large Language Models can be used for text generation, translation, question-answering tasks, etc. However, LLMs are also very large (obviously, Large language models) and require a lot of memory. This can make them challenging for small devices like phones and tablets.

Multiply the parameters by the chosen precision size to determine the model size in bytes. Let’s say the precision we’ve chosen is float16 (16 bits = 2 bytes). Let’s say we want to use the BLOOM-176B model. We need 176 billion parameters * 2 bytes = 352GB to load the model!

In other words, to load all parameter weights, we require 12(!) 32GB machines! This is too much if we ever want to make LLMs portable. Techniques for reducing the memory footprint of LLMs were developed to overcome such a struggle. The most popular techniques are:

• Quantization involves converting the LLM’s weights into a lower-precision format, reducing the memory required to store them.
• Knowledge distillation involves training a smaller LLM to mimic the behavior of a larger LLM. This can be done by transferring the knowledge from the larger LLM to the smaller LLM.

These techniques have made it possible to fit LLMs in small memory. This has opened up new possibilities for using LLMs on various devices. Today, we’ll talk about quantization (stay tuned for knowledge distillation).

Quantization

Let’s start with a simple example. We’ll need to transform 2023 to binary:

As you can see, the process is relatively straightforward. In order to store the number 2023, we’ll need 12+ bits (1 bit for the + or — sign). For the number, we might use the int16 type.

There is a big difference between storing int as binary and float as such. Let’s try converting 20.23 to binary:

As one can see, the floating part (mantissa) is calculated as the combination of 1/2^n, and cannot be calculated very precisely, even with 10 bits dedicated to the floating part. The whole number part (exponent) is set to 5 bits, covering all numbers up to 32. In total, we’re using 16 bits (FP16) for storing the closest we can to 20.23, but is it the most effective way to keep floats? What if the whole part number is much larger, say 202.3?

If we look at the standard float types, we’ll notice that to store 202.3, we’ll need to use FP32, which, from a computational perspective, is far from reasonable. Instead, we can use a bfloat16 to save the range (exponent) as 8 bits and 7 bits for precision (mantissa). This allows us to widen the scope of possible decimals without losing much precision.

To be clear, while training occurs, we need all the precision we can take. But prioritizing speed and size over the 6th decimal point makes sense for inference.

Can we decrease the memory usage from bfloat16 to, say, int8?

Zero-point and abs-max quantization

In fact, we can, and there are several approaches for such quantization:

• Zero-point quantization saves half the memory by converting a fixed range (-1, 1) to int8 (-127, 127), followed by converting int8 back to bfloat16.

• Abs-max quantization is similar to zero-point, but instead of setting a custom range (-1,1), we set it as (-abs(max), abs(max)).

Let’s take a look at how these practices are used in an example of matrix multiplication:

Zero-point quantization:

Abs-max quantization:

As one can notice, the score for large values [-1579, -1780] is quite low ([-1579, -1752] for zero-point and [-1565,-1786] for abs-max). In order to overcome such issues, we can separate outlier multiplication:

As you can see, the results are much closer to true values.

But is there a way we can use even less space without losing much quality?

To my very surprise, there is a way! What if we, instead of independently converting each number to a lower-type, would account for the error and use it for adjustments? This tecnique is called GPTQ.

Like previous quantization, we find the closest match for the decimals we can, keeping the total conversion error as close to zero as possible.

We fill the matrix row-wise in such a manner.

The result, in combination with anomaly-separate calculations, provides quite okay results:

We can now compare all the methods:

LLM.int8() methods perform pretty well! The GPTQ approach loses quality but allows the use of twice as much GPU memory as the int8 method.

In the code, you might find something similar to the following:

from transformers import BitsAndBytesConfig

# Configure BitsAndBytesConfig for 4-bit quantization
bnb_config = BitsAndBytesConfig(
 load_in_4bit=True,
 bnb_4bit_use_double_quant=True,
 bnb_4bit_quant_type="nf4",
 bnb_4bit_compute_dtype=torch.bfloat16,
)
# Loading model in pre-set configuration
pretrained_model = AutoModelForCausalLM.from_pretrained(
 model_id,
 quantization_config=bnb_config,
)

The load_in_4bit flag specifies that the model should be loaded in 4-bit precision. The bnb_4bit_use_double_quant flag specifies that double quantization should be used. The bnb_4bit_quant_type flag specifies the quantization type. The bnb_4bit_compute_dtype flag specifies the compute dtype.

To sum up, we’ve learned how decimals are stored in memory, how to reduce memory footprint with some precision loss, and how to run selected models with 4-bit quantization.

This article is part of the ongoing LangChain 101 course:

Reminder: The complete code for this article is available on GitHub.

Clap and follow me, as this motivates me to write new parts and articles 🙂 Plus, you’ll get notified when the new articles will be published.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI