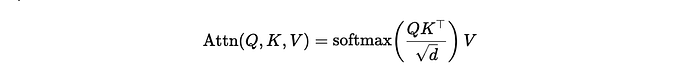
The Mathematics and Foundations behind Spectral Clustering

Author(s): Jack Ka-Chun, Yu

Originally published on Towards AI.

Spectral clustering is a graph-theoretic clustering technique that utilizes the connectivity of data points to perform clustering and is a technique of unsupervised learning.

There are 2 main types algorithms for clustering:

Compactness Clustering AlgorithmConnectivity Clustering Algorithm

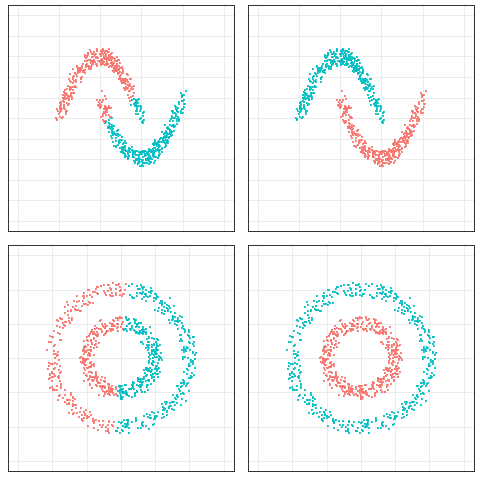
Data points that lie close to each other are divided into the same cluster and are densely compact around the cluster center. The compactness of these clusters can be measured by the distance between data points, such as in K-Means clustering, Mixture models and MeanShift clustering.

Data points that are connected or right next to each other are divided into the same clusters. Even if the distance between 2 data points is very small, if they are not connected, they will not be clustered together, e.g., the technique of this article topics spectral clustering.

Left: Compactness; Right: Connectivity

Spectral clustering involves some basic knowledge of linear algebra, which includes linear transformation, eigenvectors, and eigenvalues. Thus, before we start learning the algorithm of spectral clustering, let us recall the memory of linear transformation.

Definition

Spectral clustering is different from the traditional machine learning process because it is not inherently a predictive model-based learning method, but a based-on graph-theoretic clustering method, so the steps of “defining model functions” → “defining loss functions” →… Read the full blog for free on Medium.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI