SUPPORT VECTOR MACHINES

Author(s): Data Science meets Cyber Security

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

SUPERVISED LEARNING METHODS: PART-3

SUPPORT VECTOR MACHINES:

Let’s first comprehend the example in order to get off to a better start before moving on to the term.

Consider the following scenario: An online beauty firm wishes to develop a classification engine to analyze the products with the best sales across the five categories of SPA, skincare, hair care, makeup, and body care.

NOTE: In machine learning, whenever we work with supervised learning algorithms, we always deal with the matrix (total no. of rows and columns) and target i.e (categories), however in unsupervised learning, the target is not available, so we simply work with the matrix.

WHAT OUGHT TO BE DONE IN SUCH CIRCUMSTANCES?

Our initial thought is to utilize the classification method to group items to understand, identify, and classify the concepts and things into predetermined groups which is basically the process of classification.

The first thing we’ll do is set the target vector, which is a multi-class classification. This involves deciding which products belong in which categories first and categorizing them accordingly. This means we have a lot of rows and columns, which increases the risk of overfitting. In situations like this, we need an algorithm that can help us accomplish our goal while also lowering the risk of overfitting. The SUPPORT VECTOR MACHINE algorithm enters the picture at this point.

An algorithm called SUPPORT VECTOR MACHINES can handle many columns and many predictors for a very modest number of trades.

SUPPORT VECTOR MACHINE is divided into two categories:

1. Linear support vector machines
2. Non-linear support vector machines

1. LINEAR SUPPORT VECTOR MACHINES:

When a dataset can be divided into two classes by means of a single straight line, it is said to be linearly separable, and the classifier utilized is known as a Linear SVM classifier.

Let’s start with the algorithm’s fundamental building block, maths, in order to grasp it from the ground up:

THE DOT PRODUCT

Everyone would naturally be an expert at this as we all learned how to compute the dot product in our early years.

The dot product is also known as the projection product. Why? Let’s see

THIS AMAZING ARTICLE WHICH I FOUND ON THE INTERNET IS THE BEST EXAMPLE OF THIS QUESTION:

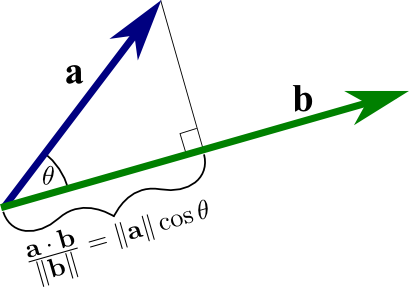
The projection of ‘a’ onto ‘b’ is the dot product of the vectors ‘a’ (in blue) and ‘b’ (in green), divided by the magnitude of ‘b’. The red line segment from the tail of ‘b’ to the projection of the head of ‘a’ on ‘b’ serves as an example of this projection.

THE DOT PRODUCT AND THE HYPERPLANE:

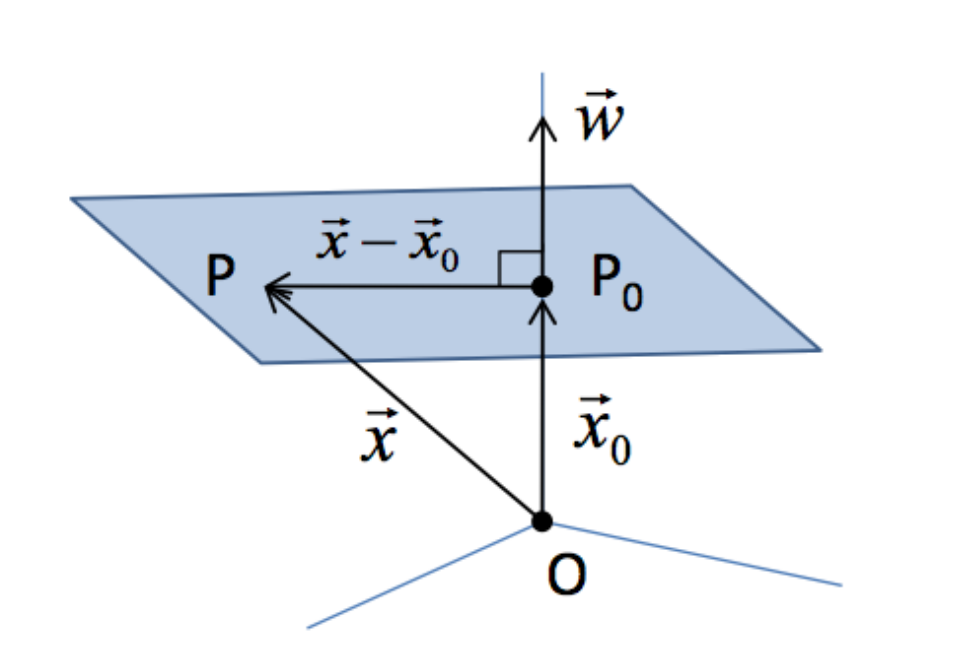
WHAT EXACTLY A HYPERPLANE IN SVM MEANS?

In support vector machines, the hyperplane is a decision boundary that separates the two classes. The various classes may be identified by a data point that lies on each side of the hyperplane, as seen in the linear support vector machine graph above. The amount of features in the datasets determines the hyperplane’s dimension.

The most basic equation of the plane. I.e

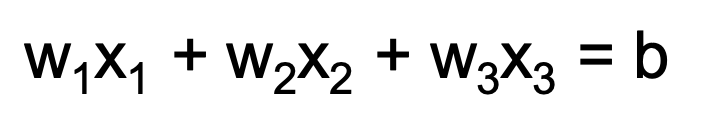
ALTERNATIVE SPECIFICATION

• Specifying a point and a vector perpendicular.
• Let P & P0 be two points on a hyperplane.
• Let x & x0 be two vectors supporting the hyperplane.

Consider the vector ‘w’ which is orthogonal to the hyperplane at x0

• (x- x0) must lie on the hyperplane → w must be orthogonal to (x- x0)
• w(transpose)(x-x0) = 0
• w(transpose)x = -w(transpose)x0
• w(transpose)x = b

LINEAR CLASSIFIERS:

The job of distinguishing classes in feature space can be seen as binary classification:

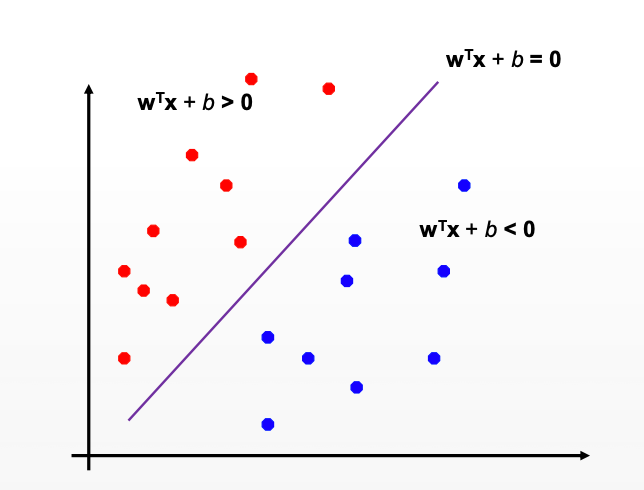
MARGIN OF CLASSIFIER IN ORDER TO CLASSIFY DATA?

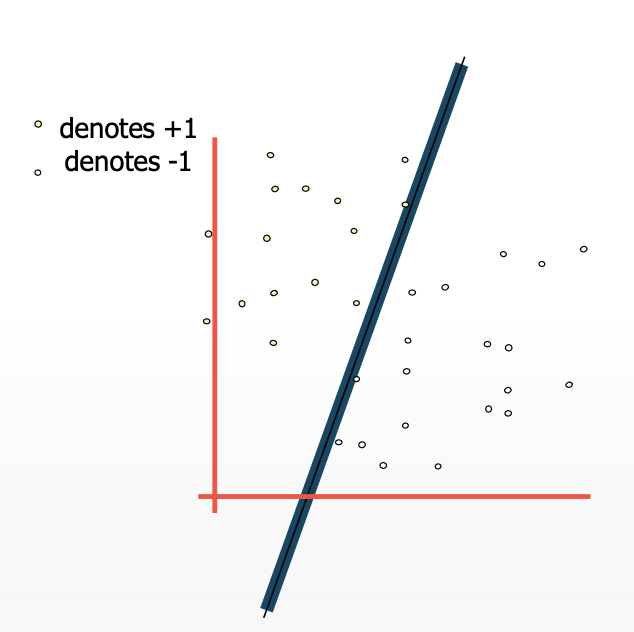
The margin is the separation between the line and the nearest data points. The line with the biggest margin is the best or ideal line that can divide the two classes.

MAXIMUM MARGIN :

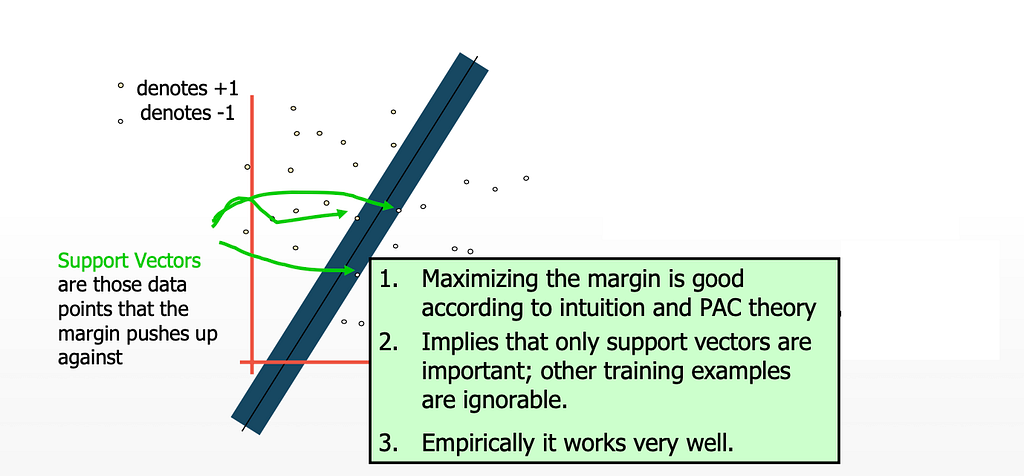
The linear classifier with the greatest margin is known as the largest margin linear classifier.

This is the simplest kind of SUPPORT VECTOR MACHINE, also known as the LINEAR SUPPORT VECTOR MACHINE.

Now that we’re talking about real-world scenarios, we can see that the data points in these situations are frequently not linearly separable and also prone to noise and outliers, so we cannot actually classify this data using the previous formulations.

WHY ARE HYPERPLANE AND MARGIN IMPORTANT CONCEPTS IN SVM?

The margin is a term that may be used to describe the separation between the line and the nearest data point. The line with the widest margin is the best or ideal line that may be used to divide the two classes. We referred to this as the MAXIMAL MARGIN HYPERPLANE.

HOW TO FIX THE FORMULATION TO HANDLE THE NOISE AND OUTLIERS:

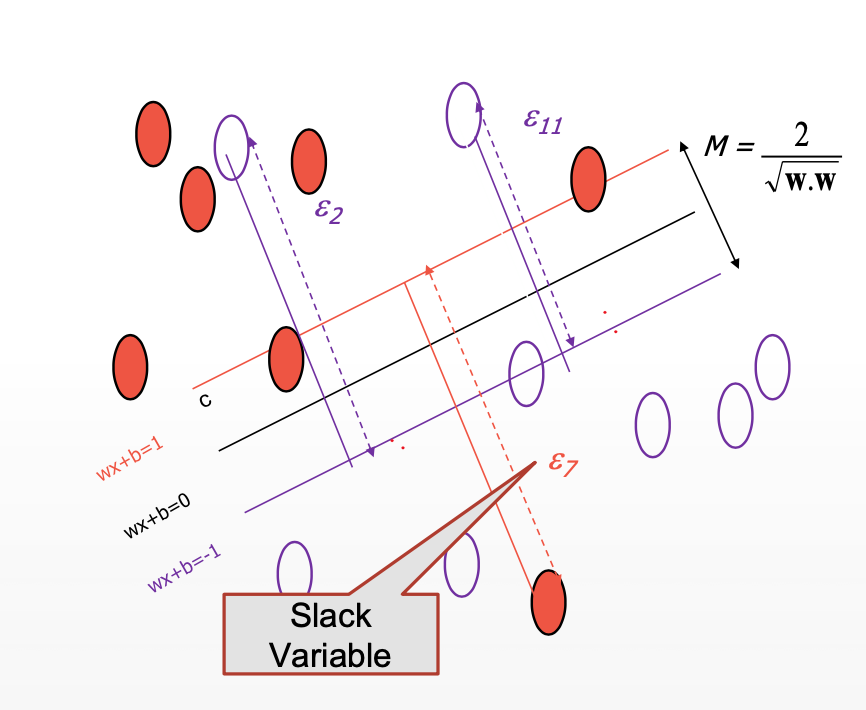
THE FORMULA USED TO FIX THE NOISE AND OUTLIER:

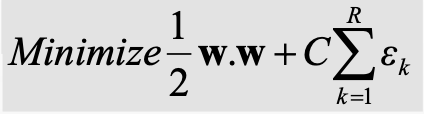
Now moving forward the only thing that might possibly trouble a human intellect when analyzing the given figure is what that “C” means ? and why did we choose that?

Okay, then let’s get started.

The ‘C’ here stands for the SUPPORT VECTOR PARAMETER –

To conveniently classify fresh data points in the future, the SVM algorithm seeks to identify the optimal line or decision boundary for classifying n-dimensional space. The optimal choice boundary is a hyperplane.

The higher dimensional space is created using SVM by selecting the nearby remarkable points. The approach is known as the Support Vector Machine, and these extreme situations are known as support vectors.

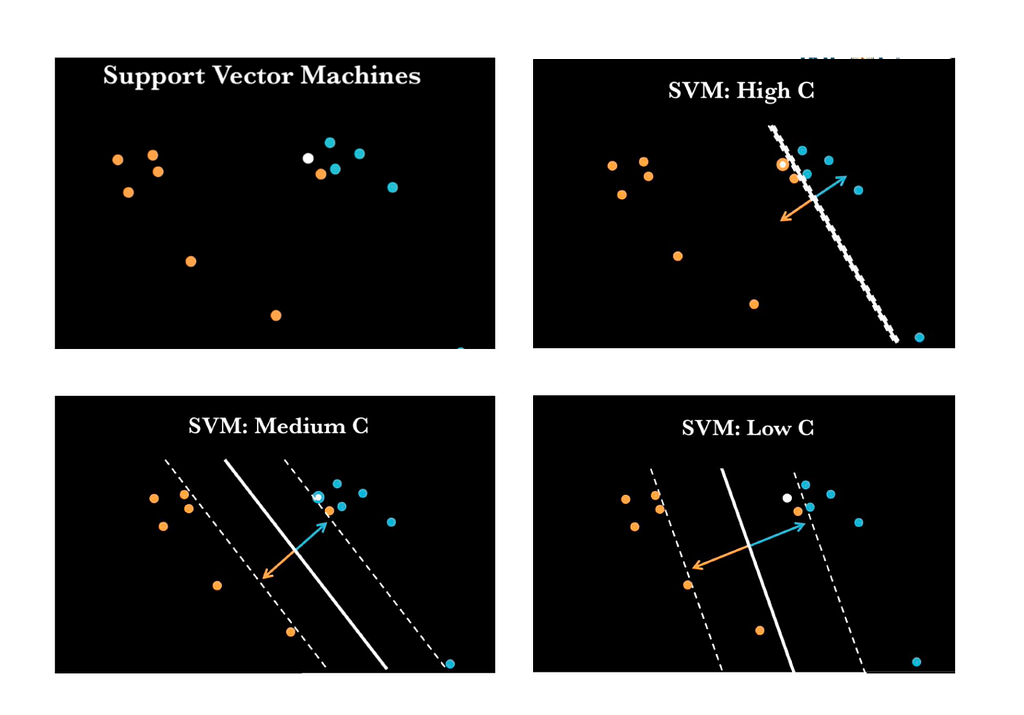
SVM PARAMETER — C:

1. Controls training error.
2. It is used to prevent overfitting.
3. Let’s play with C. (because why not 😁)

2. NON-LINEAR SUPPORT VECTOR MACHINES:

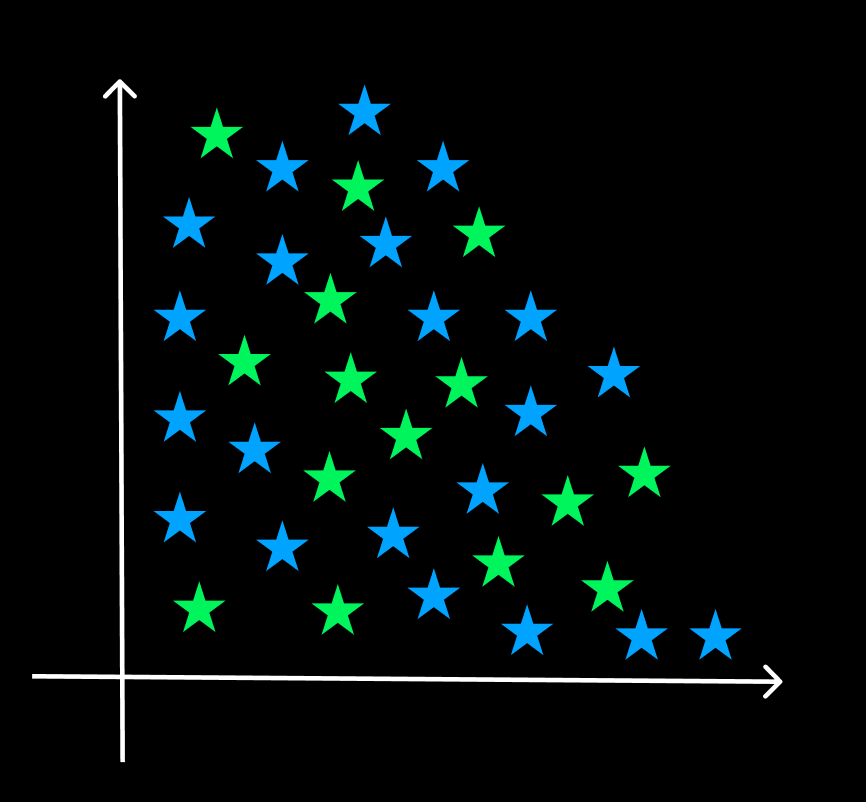
Non-Linear Classification is the process of classifying situations that cannot be separated linearly. We divide data points using a high-dimensional classifier in nonlinear SVM.

Let’s take a look at the most famous trick used in non-linear SVM

THE KERNEL TRICK:

A kernel is a technique for introducing a two-dimensional plane into a higher-dimensional environment, curving it there. A kernel is a function that transforms a low-dimensional space into a higher-dimensional one.

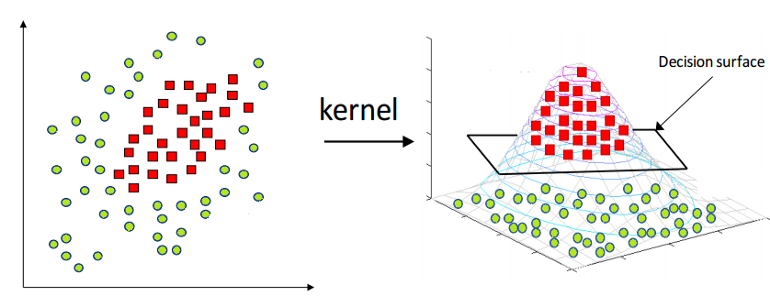
WHY KERNEL TRICK?

SUPPORT VECTOR MACHINE has trouble categorizing non-linear data. The use of the Kernel Trick is the simple fix in this situation. A kernel trick is a straightforward technique that involves projecting nonlinear data into a higher dimension space where it may be linearly split by a plane, making it easier to categorize the data. The Lagrangian formula and Lagrangian multipliers are used to mathematically achieve this. (More information is provided in the maths part that follows.)

SUMMING UP THE STEPS:

1. Pre-process (scaling, numerical mapping, etc.) training data.
2. Pick up Kernel Trick to fix the trouble caused while categorizing the non-linear data.
3. Use Cross-Validation to find the best C and σ parameter values.
4. Use the best C, σ to train on the entire training set.
5. Test.

FEW POINTS TO REMEMBER (IMP ONES) :

1. Support Vector Machines (SVMs) work very well in practice for a large class of classification problems.
2. SVMs work on the principle of learning a maximum margin hyperplane which results in good generalization.
3. The basic linear SVM formulation could be extended to handle noisy and non-separable data.
4. The Kernel Trick could be used to learn complex non-linear patterns.
5. For better performance, one has to tune the SVM parameters such as C, and kernel parameters using a validation set.

I hope this blog makes the math and primary idea behind the support vector machine obvious.😎

STAY TUNED FOR THE NEXT BLOG, WHERE WE’LL DISCUSS HOW TO IMPLEMENT THE SVM IN PYTHON THROUGH AN AMAZING CASE STUDY.❤️

FOLLOW US FOR THE SAME FUN TO LEARN DATA SCIENCE BLOGS AND ARTICLES:💙

LINKEDIN: https://www.linkedin.com/company/dsmcs/

INSTAGRAM: https://www.instagram.com/datasciencemeetscybersecurity/?hl=en

GITHUB: https://github.com/Vidhi1290

TWITTER: https://twitter.com/VidhiWaghela

MEDIUM: https://medium.com/@datasciencemeetscybersecurity-

WEBSITE: https://www.datasciencemeetscybersecurity.com/

— Team Data Science meets Cyber Security ❤️💙

---

SUPPORT VECTOR MACHINES was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI