StyleGAN3: Allias-Free GAN

Author(s): Albert Nguyen

Originally published on Towards AI.

Have you ever thought of a movie that is totally generated by AI?

Recent advancements in generative AI have shown promising results in controllable image generation. Generators like StyleGAN2 can produce realistic images. See ‘This Person Does Not Exist — Random Face Generator.” Yet, these models are incapable of generating good-quality videos and animation due to a phenomenon that causes features to stick in one place. These features appear to have some fixed position features, making these generators unsuitable for ‘movie generating.’
StyleGAN3 paper addresses the causes for this issue: current networks have unintentionally produced ‘pixel reference’ in the intermediate layers. One of the main reasons is aliasing, which causes different signals to become indistinguishable. This work focuses on removing the generator network’s aliasing while maintaining the generated images’ quality.

Signal in Generator network

Before stepping further into this article, we should understand what signal the model is receiving. The signal refers to a feature map that controls the content the generator will draw on the image — for example, the amount of hair at some pixels. Under the context of the StyleGAN generator, it is the information from the intermediate latent codes.

However, the generator can only operate on the discrete representation of the signals. A common problem when doing this is aliasing, where different continuous signals can be sampled into the same discrete signal. This is the issue causing the model to create pixel references, making the texture stuck in one place.

It is said in the Nyquist-Shannon sampling theorem. The sampling rate must be at least twice the signal’s highest frequency to sample a continuous signal. The aliasing occurs when the sampling process does not follow the theorem.

Operate on the continuous signal.

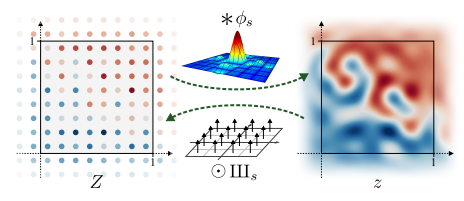
The goal of StyleGAN3 is to transform the continuous signal by operating on the corresponding discrete signal with operation F. Let’s say Z is the discrete representation of the continuous signal z. We can deduce z from Z and Z from z using a low-pass filter and Dirac comb IIIs.

The problem turns into enforcing the model equivariance.

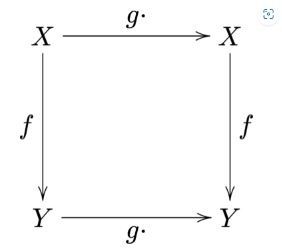
It means that the model is operating on the correct continuous signals. We have the model operation, f, on the continuous signal:

Where s’ and s are the sampling rate of the output and input, in other words, the 1 / (image’s resolution). Luckily, most of the operations we currently use, such as convolution, up/down sampling, etc., are proved to be equivariance. For convolution, the kernels have to be radially symmetric.

At this point, we have yet to make any modifications to the generator. But the equation above only holds when there is no aliasing, meaning that the operation F(Z) introduces no signal with a higher frequency than half the sampling rate of s’. Our problem is left with layers like up/down sampling (changing output sampling rate) and non-linearity layers (provide high-frequency features)

Resolve non-linearity problem with low pass filtering

Non-linearity layers are essential ingredients for neural networks. They allow models to learn more complex, non-linear functions. Indeed, if we don’t have any non-linearity layers in a neural network, we can actually compress that whole network into a single matrix.

However, these layers sometimes bring us troubles as well. In this case, for example, the ReLU layer may introduce arbitrary high-frequency signals:

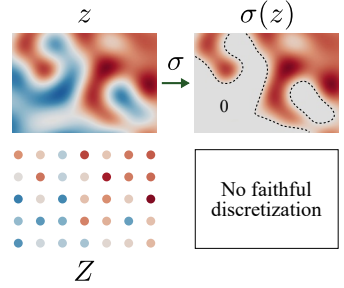
Now, remember that our sampling rate is inversely proportional to our discrete feature map resolution. Thus, this sampling rate remains unchanged after the ReLU. However, the continuous feature map appears to have a high-frequency signal (the jump from white to red region). This may lead to aliasing as the sampling rate will not be higher than twice the highest frequency.

To resolve the problem above, the author suggests using a low-pass filter to reduce the frequency of the continuous signal. It is just simply removing the high-frequency components:

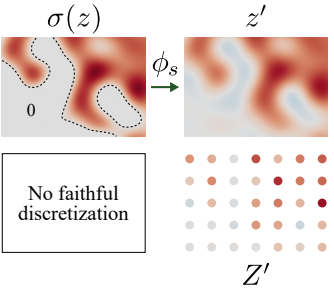
To the best of my knowledge, one way to do this is by using the Fast Fourier Transform 2D and zero out all the high-frequency components. Let ψs be the ideal low-pass filter, we have the model’s operation on continuous signal to be:

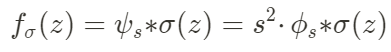
and our discrete operation becomes:

Up/Down sampling

These sampling layers do not change our continuous signal. But instead, they change our feature map resolution, which means the sampling rate. In fact, there is no problem with the up-sampling layers as they increase the sampling rate, which is a good thing. However, the down-sampling decreased our sampling rate.

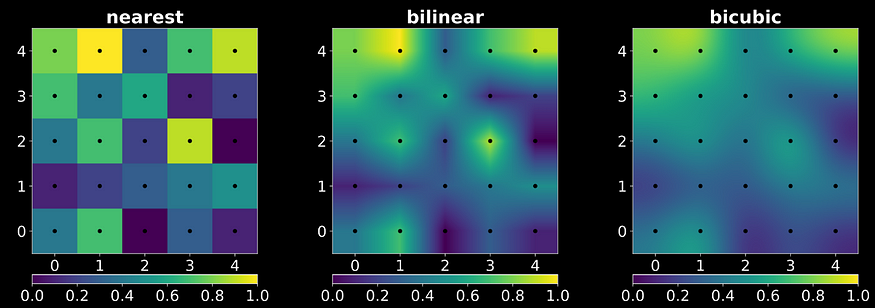
We can do the same as we did while resolving the non-linearity problem by using a low-pass filter to remove frequencies above the output bandlimit. Our continuous and discrete operations are:

Practical modification

According to the analysis of signal processing operation of the generator network, the author proposed many changes to the generator:

The generator operates on Fourier features that contain phases and frequencies. This is an essential bridge between the continuous and discrete representations of the signal. Furthermore, the goal is to make the generator equivariant w.r.t. the continuous signal, and metrics to evaluate and quantify the equivariance are given by:

1. For translation equivariance, the work reports the peak signal-to-noise ratio (PSNR) between two sets of images (obtained by translating the input and output of the synthesis network:

2. For rotation equivariance,

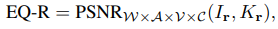
Conclusion

In the paper, the author found a problem in the StyleGAN2 generator that makes it incapable of generating video and animation. The generator turned out has been operating on an unfaithful discrete representation of the continuous signal, thus forcing it to provide pixel references for some features (typically high-frequency features such as hair, edges, etc.) The reason for this is aliasing in unfaithful discrete signals, causing different signals can have the same representation.

In StyleGAN3, the author proposed changes to the generator to remove these aliasing. By carefully considering the model’s operations on the continuous signal, the pixel references are removed, and also improve the FID of the synthesis data.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI