Savitzky-Golay Filter for data Smoothing

Author(s): Mohneesh S

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Machine Learning

Most underrated technique while Data Preprocessing

The unwritten rule in any ML/AI Engineer or Data scientists’ life is that “spend a healthy amount of time on data cleaning and preprocessing”, because “Garbage in — garbage out”. While preparing the dataset for training/modeling we forget to account for outliers in the data.

Outliers and How to Deal with Them

Outliers are points in the data that are at the extremes of their respective variable ranges. eg: a height of 7 ft is rarely seen in any dataset containing heights of some X people. In this particular example, the height is either a data recording inconsistency or the correct measurement, either way, it's hard to know for sure and it impacts the model very much if not treated beforehand.

There are a number of solutions that can be applied in such cases. We could use anomaly/outlier detection algorithms to remove them. There are many different kinds of algorithms to do this which I won’t be covering in this article as it's a very huge area of study which cannot be incorporated in a single article.

There is another method known as data smoothing which tries to retain the information given through these abnormal points and not completely remove them. It's a best practice to remove points that are at the very extremes(significantly different from the data) for example a height of 20 ft, is surely an outlier and shouldn’t be sampled when training your models. Smoothing techniques are better when there are abnormal data every once in a while in the data, for example, sudden spikes in AQI time series data, which could be true, but treating them is an important step.

Savitzky-Golay Filter

This is where this amazing low pass filter comes into the picture. This is mostly used in signal processing as a filter for signal fluctuations. This could very well be used in smoothing out the data as well. This filter tries to approximate the original function removing the useless fluctuations/ noise from the data which can very well misguide your model.

How Does It Work

For folks who are familiar with the nD convolution concept in Deep learning, this filter just works like that. For those who aren’t familiar, this works pretty much like a moving average technique, but we can specify the order of polynomial with which the data is fitted.

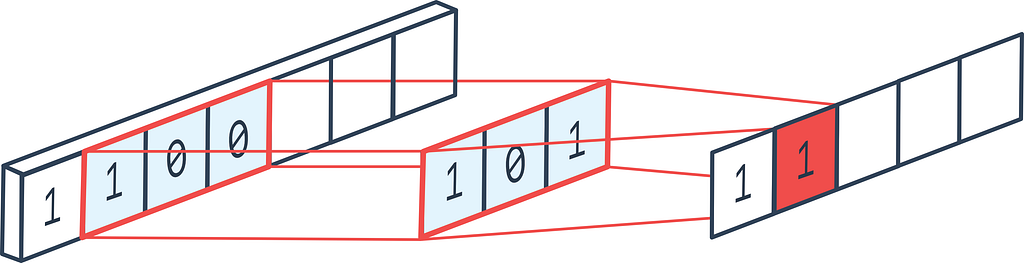
This filter is widely used in Analytical Chemistry and Electronics, and mostly overlooked in Machine learning, (the reason I decided to write about this). Basically, this filter is convolved around subsets of the dataset, each subset is fitted with a polynomial function that tries to minimize the fit error of that particular subset, this in turn gives us a new set of points that are smoothed out than before. (basically moving average transformation with extra steps)

For the mathematical derivation refer Here.

Implementation in Python

Let’s look at a real-world example that would make this clear for us. We will use the savgol_filter function from scipy.signal package. Take a look at the below simple code that I wrote to demonstrate how this filter works. The optimal window_size and polynomial_order are found out from experimenting with different values. Taking higher window sizes will change the meaning of the data too much, so small odd-numbered windows are recommended, although these are determined based on the domain, situation, and various experiment results.

I have taken 5 days of data of the DOGE — USD data from yahoo finance and have used the highs of all days to showcase how we can smooth data still retaining the original structure of the dataset

This produces the following plot :

Conclusion

In real-world examples, this works pretty well and is very flexible according to our needs. This is really overlooked in this field and hopefully, I have shed some light on this concept. Please refer to the original paper if the idea interests you and want to find out more about this.

Thank you for reading through. If you have read it till here, I am honored.

Savitzky-Golay Filter for data Smoothing was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI