Introduction to Numpy in Python

Last Updated on October 29, 2021 by Editorial Team

Author(s): sonia jessica

Programming

What is NumPy?

NumPy stands for numeric python, a Python module that allows you to compute and manipulate multi-dimensional and single-dimensional array items. It comes with a high-performance multidimensional array object as well as utilities for working with them.

In 2005, Travis Oliphant created the NumPy package by combining the features of the ancestral module Numeric with the characteristics of another module Numarray. NumPy implements multidimensional arrays and matrices as well as other complex data structures. These data structures help to compute arrays and matrices in the most efficient way possible. NumPy allows you to conduct mathematical and logical operations on arrays. Many other prominent Python packages, like pandas and matplotlib, are compatible with Numpy and use it.

Need to use NumPy in Python?

NumPy is a valuable and efficient tool for dealing with large amounts of data. NumPy is quick; thus, it’s easy to work with a vast amount of data. Data analysis libraries like NumPy, SciPy, Pandas, and others have exploded in popularity due to the data science revolution. Python is the most simple language in terms of syntax, and is the priority for many data scientists; therefore, NumPy is getting popular day by day.
Many mathematical procedures commonly used in scientific computing are made quick and simple with Numpy, including:

• Multiplication of Vector or Matrix to Vector or Matrix.
• Operations on vectors and matrices at the element level (i.e., adding, subtracting, multiplying, and dividing by a number )
• Applying functions to a vector/matrix element by element ( like power, log, and exponential).
• NumPy has functions for linear algebra and random number generation built-in.
• NumPy also makes matrix multiplication and data reshaping simple.
• Multidimensional arrays are implemented efficiently using NumPy.
• NumPy arrays in Python give capabilities for integrating C, C++, and other languages. It’s also useful in linear algebra and random number generation, among other things. NumPy arrays can also be used to store generic data in a multi-dimensional container.
• It’s faster than standard Python arrays, which don’t have NumPy’s pre-compiled C code(Precompiled code is a header file that is compiled into an intermediate form that is faster to process for the compiler).

Installation of NumPy

Go to your command prompt and run “pip install numpy” to install Python NumPy. Once the installation is complete, simply go to your IDE (for example, VS Code, Jupyter Notebook, PyCharm) and type “import numpy as np” to import it; now you are ready to use NumPy.

What is a NumPy Array?

The Numpy array object is a strong N-dimensional array object with rows and columns. NumPy arrays can be created from nested Python lists, and their elements can be accessed. It refers to a group of items that are all of the same types and can be accessed using zero-based indexing. Every item in a ndarray is the same size as the memory block. Each entry in ndarray is a data-type object (called dtype).

Types of Numpy Array:

• One-Dimensional NumPy array
  A one-dimensional array has only one dimension of elements. In other words, the one-dimensional NumPy array should only contain one tuple value.
  Example:

# One-Dimensional Array
import numpy as np
val=np.array([1, 5, 2, 6])
print(val)

Implementation:-

Explanation: print() function is used to print the whole array provided.

• Multi-Dimensional NumPy Array
  A multi-dimensional array can have n dimensions of elements. In other words, the multi-dimensional NumPy array can contain a number of tuple values.
  Example:

# Multi-Dimensional Array
import numpy as np
val=np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val)

Implementation:

Explanation: print() function is used to print the whole array provided.

Accessing Element in the Array

Indexing or accessing the array index in a NumPy array can be done in a variety of ways.
1. Slicing is used to print a range of an array. The built-in slice function is used to create a Python slice object by passing start, stop, and step parameters to it. Slicing an array involves establishing a range in a new array used to print a subset of the original array’s elements. Because a sliced array holds a subset of the original array’s elements, editing content alters the original array’s content.
Example 1:

# Accessing Array Element
import numpy as np
val=np.array([1, 5, 2, 6])
# Zero based indexing
print(val[1])
val_mul=np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val_mul[1][1])

Implementation:

Explanation: Here we are accessing the 1st index value of the 1-D array via writing val[1] and accessing the value in the 2nd row and 2nd column of the 2-D array as the arrays have zero-based indexing.

Example 2:

#Accessing Range of Elements 
#in array using slicing
val_mul=np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
slice_val = val_mul[:2, :2]
print (“First 2 rows and columns of the array\n”, slice_val)
Implementation:

Implementation:

Explanation: Here we are trying to access the values in rows and columns starting from 1st row to 2nd row by writing “ :2 ” as the first argument and similarly accessing all the values corresponding to those rows and having columns from starting to the 2nd.

Example 3:

val_mul1=np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6),(1, 5, 0, 1),(7, 3, 3, 0)])
slice_step_row = val_mul1[::2, :2]
print (“All rows and 2 columns of the array with step size of 2 along the row\n”, slice_step_row)

Implementation:

Explanation: Here we are trying to access the values in rows and columns starting from 1st row to end row with a step size of 2 which means the difference between consecutive rows to be 2 by writing “::2 ” as the first argument and similarly accessing all the values corresponding to those rows and having columns from starting to the 2nd.

Example 4:

# Accessing multiple elements at one go
val_mul1=np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6),(1, 5, 0, 1),(7, 3, 3, 0)])
mul_idx_arr = val_mul1[
 [1, 2, 2, 3], 
 [1, 2, 3, 3]
 ]
print (“\nAccessing Elements at multiple indices (1, 1),(2, 2), (2, 3), (3, 3) →”, mul_idx_arr)

Implementation:

Explanation: Here we are trying to access the values from the array which are present at the indexes (1,1),(2,2),(2,3), and (3,3).

2. Another type of accessing technique is the boolean array indexing where we can give the condition where elements that follow the condition are printed.

Example:

# Boolean array indexing
val_mul=np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6),(1, 5, 0, 1),(7, 3, 3, 0)])
condition = val_mul > 3 
res = val_mul[condition]
print (res)

Implementation:

Explanation: Here we are accessing the values which follow the given conditions i.e. the value of the element should be greater than 3.

Frequently used Operations on Numpy Array

• ndim– This operation is used to compute the dimension of the array.

Example:

# Dimension of the array
val1 = np.array([1, 5, 2, 6])
print(val1.ndim)

# 2-D array
val2 = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val2.ndim)

Implementation:

Explanation: Here val1 is a 1-D array having values 1,5,2 and 6 therefore we are getting value 1 for val1.ndim and val2 is a 2-D array
3 4 2 5
3 6 2 4
1 5 2 6
Therefore we are getting value 2 corresponding to val2.ndim

• Size — This operation is used to calculate the number of elements in the array.

Example:

# Calculate Array Size 
val2 = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val2.size)

Implementation:

Explanation: Here val2 contains 12 values 3, 4, 2, 5, 3, 6, 2, 4, 1, 5, 2, 6 therefore we are getting the size of the val2 array as 12.

• Shape — This operation is used to calculate the shape of the array.

Example:

# Calculate Array Shape 
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.shape)

Implementation:

Explanation: Here Val array is a 2-D array
3 4 2 5
3 6 2 4
1 5 2 6
It has 3 rows and 4 columns and val.shape is used to get the size corresponding to each dimension.

• Reshape — Reshape is used to reshape the array according to the given parameters

Example:

# Reshape the Array
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val)

val=val.reshape(2,6)
print(val)

Implementation:

Explanation: reshape function helps us to reshape the array and fill the values of the array correspondingly. Here we have 12 values and we want to reshape the array from (3,4) to (2,6) so now there would be only 2 rows and 6 columns.

• Transpose — T operator is used in getting the transpose of an array.
  Example:

# Transpose of an array
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.T)

Implementation:

Explanation: When we need to replace all the rows of an array with the columns and columns with rows then we need to call the val.T to get the transpose of the array. In transpose, the shape of the array changes as now number of rows becomes a number of columns and vice versa. As here 3, 4, 2, 5 was the first row initially but after transpose, it becomes the 1st column.

• Ravel — ravel is used to convert the array into a single column
  Example:

# Convert Array to Single Column
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.ravel())

Implementation:

Explanation: When we want to convert the array to a 1-D array we use the ravel function as it combines all the values of the array as in the above example we had initially a 2-D array of 3 rows and 4 columns but after applying the ravel function we gets the 1-D array of 12 values.

• Itemsize: Itemsize is used to compute the size of each element in bytes.
  Example:

# Calculate Array Itemsize
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
# size of each element in bytes
print(val.itemsize)

Implementation:

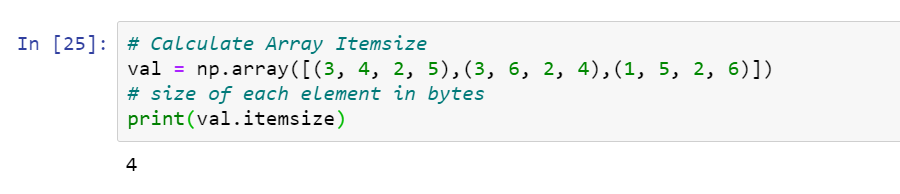
Explanation: When we want to get the size of each element in bytes we use (array_name.itemsize) as in the above example the data type is int32 which means integer of 32 bits and as we know that 1 byte is equal to 8 bits and hence it is 4 bytes in size.

• Dtype– Dtype is used to get the data type of the elements in the array.
  Example:

# Calculate Data type of each element
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.dtype)

Implementation:

Explanation: When we want to compute the data type of the elements present in the array we use val.dtype which gives us the data type here in the above example the values of the array are integer so the data type given is int32 which means it represents an integer of 32 bits.

• np.zeros()/np.ones() — ones() and zeros() functions of numpy are used to generate arrays having all 1’s and 0’s respectively.
  Example:

# Generating array having all 1's
val = np.ones(3)
print(val)
 
# Generating array having all 0's
val0 = np.zeros(3)
print(val0)

Implementation:

Explanation: When we want to generate an array having all 1’s or 0’s we use the above-given functions which helped us generate an array of size n. Here we gave the size of the array as 3 so an array of size 3 having all 1’s and 0’s is generated.

– linspace — The linspace function is used to generate an array containing elements distributed equally in a given range. It takes 3 parameters to start and end of the range and the number of elements to be present in the array.

Example:

# Linspce generate 8 numbers present in range 2–5
val = np.linspace(2,5,8)
print(val)

Implementation:

Explanation: When we want to generate an array having specific order like in range x to y and size of the array to be n then we use linspace function as here we wanted to generate an array of size 8 having values equally spaced between range 2 to 5.

• Max — Max is used in getting the maximum element across the whole array.

Example:

# Find maximum element in whole array
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.max())

Implementation:

Explanation: When we want to calculate the maximum of all elements of the array we can simply write array_name.max() and get the maximum element as here we get 6 which is the maximum of all the elements.

• Min — Min function is used in getting the minimum element across the whole array.

Example:

# Find minimum element in whole array
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.min())

Implementation:

Explanation: When we want to calculate the minimum of all elements of the array we can simply write array_name.min() and get the minimum element as here we get 1 which is the minimum of all the elements.

• Sum — Sum function is used to get the total of all the elements of the array.

Example:

# Sum of all elements in whole array
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val.sum())

Implementation:

Explanation: When we want to calculate the sum of all elements of the array we can simply write array_name.sum().

• np.sqrt() — This function is used to get the square root of all the elements of the array.

  Example:

# Used to calculate square root of each element
val=np.array([1, 4, 9])
print(np.sqrt(val))

Implementation:

Explanation: When we want to calculate the square root of each value of an array we can simply write np.sqrt(array_name) and we get the corresponding square roots to each and every value e.g. 2 corresponding to 4 and 3 corresponding to 9.

• np.std(): This function is used to calculate the standard deviation of all the elements of the array.

Example:

# Used to calculate standard deviation of all elements
val=np.array([1, 4, 9])
print(np.std(val))

Implementation:

Explanation: When we want to find the standard deviation of all the values of the array we do not need to do the hectic math calculation for calculating the standard deviation, we can simply write (np.std(array_name)).

• Summation operation on the array — When we need to add some particular number n to all the elements of the array or one array to another array.

Example1:

# Add number 3 to all elements of array val
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val+3)

Implementation:

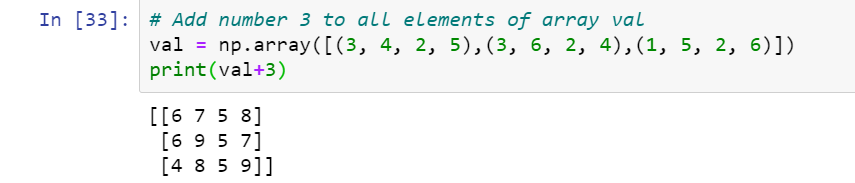
Explanation: When we want to add value n from each value of array we can simply write (array_name+n).

Example 2:

# Add array val to another array val1
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
val1 = np.array([(4, 4, 8, 2),(9, 0, 3, 5),(6, 8, 3, 3)])
print(val+val1)

Implementation:

Explanation: When we want to find the addition of 2 arrays we can simply write (array1+array2) to get the addition of arrays but just keep in mind that the dimensions of both the arrays must be the same.

• Subtraction operation on the array — When we need to subtract some particular number n to all the elements of the array or one array from another array.

Example1:

# Subtract number 3 from all elements of array val
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val-3)

Implementation:

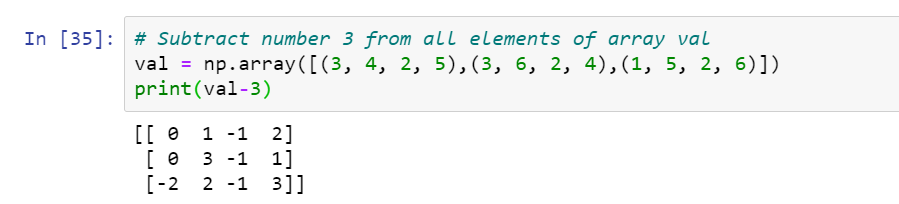
Explanation: When we want to subtract value n from each value of array we can simply write (array_name-n).

Example 2:

# Subtract array val from another array val1
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
val1 = np.array([(4, 4, 8, 2),(9, 0, 3, 5),(6, 8, 3, 3)])
print(val1-val)

Implementation:

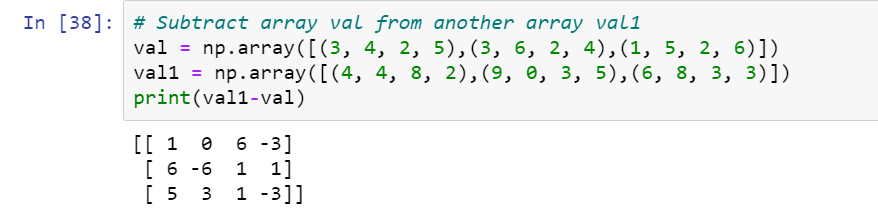
Explanation: When we want to find the difference between 2 arrays we can simply write (array1-array2) to get the difference of arrays but just keep in mind that the dimensions of both the arrays must be the same.

• Power of each element of the array raised to number n:

Example:

# Power of each element of the array raise to 3
# Cube of each element
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val**(3))

# Power of each element of the array raise to 0.5
# Square root of each element
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val**(0.5))

Implementation:

Explanation: Here we are raising to the power of 3 each and every value of the array and printing it.When we want to raise to the power of n each value of array we simply write (array_name)**n to raise to the power of each and every value of the array by value n.

• Modify each element:

Example:

# Multiply each element of the array by 3
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val*(3))

# Divide each element of the array by 3
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(val/3)

Implementation:

Explanation: Here we are multiplying each and every value of the array by 3 and printing it. Similarly, when we want to divide each value of array we simply write (array_name)/n to divide the array by value n.

• np.sort() — This function is used to sort the array and takes the argument axis which allows sorting the array row-wise and column-wise when initialized with values 1 and 0 respectively.

Example1:

# Sort the array row-wise
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
print(np.sort(val,axis=1))

Implementation:

Explanation: Here we are sorting the values of the array row-wise as we have provided the value of the axis as 1.

Example2:

# Sort the array column-wise
val = np.array([(3, 4, 2, 5),(3, 6, 2, 4),(1, 5, 2, 6)])
np.sort(val,axis=0)

Implementation:

Explanation: Here we are sorting the values of the array column-wise as we have provided the value of the axis as 0.

What to do next?

The NumPy library in Python is one of the most widely used libraries for numerical computation. We looked at the NumPy library in-depth with the help of various examples in this article. We also demonstrated how to utilize the NumPy library to do several linear algebra operations. I recommend that you practice the examples provided in this post. If you want to work as a data scientist, the NumPy library is one of the tools you’ll need to master to be a successful and productive member of the profession. Learn More.

---

Introduction to Numpy in Python was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Published via Towards AI