GELU : Gaussian Error Linear Unit Code (Python, TF, Torch)

Author(s): Poulinakis Kon

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

GELU : Gaussian Error Linear Unit Code (Python, TF, Torch)

Code tutorial for GELU, Gaussian Error Linear Unit activation function. Includes bare python, Tensorflow and Pytorch code.

GELU Activation Function

Gaussian Error Linear Unit, GELU, is the most-used activation function in state-of-the-art models including BERT, GPT, Vision Transformers, etc..

If you want to understand the intuition and math behind GELU I suggest you check my previous article covering the GELU paper (GELU, the ReLU Successor? Gaussian Error Linear Unit Explained). The motivation behind GELU is to bridge stochastic regularizers, such as dropout, with non-linearities, i.e., activation functions. Huge transformer models like BERT and GPT made GELU activation function very popular.

Is GELU, the ReLU successor ?

GELU Math Formula

Gaussian Error Linear Unit activation function output value is not deterministic, but rather stochastically relies on the input’s value.

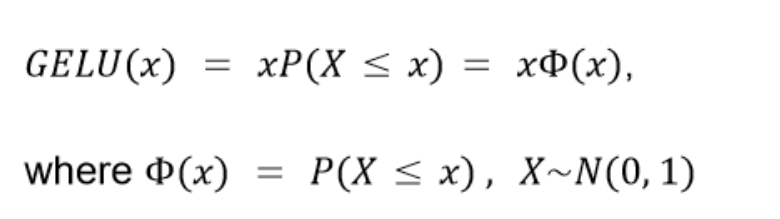
GELU activation can be approximated by the two formulas below. The first approximation is more accurate, while the second less precise but faster. We use the first formula to write a Python implementation.

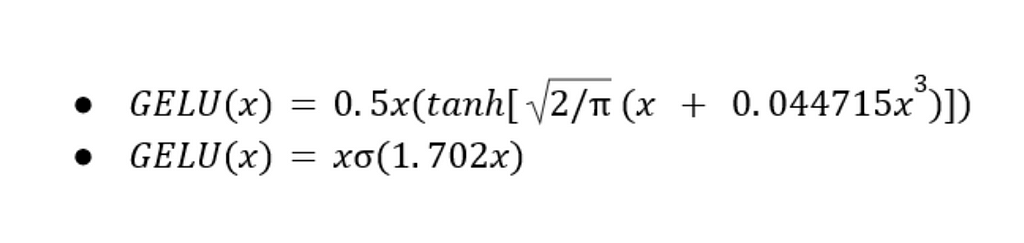
GELU in Python

To get the exact formula we need to compute the Gaussian Error Function (erf). This is the most time consuming but also most precise implementation. For a faster implementation, we use the approximation based on tanh() because it’s more precise. The Python code below covers both.

GELU in Tensorflow -Keras

Tensorflow offers the activation function in their tf.keras.activations module and you can import it as

from tensorflow.keras.activations import gelu

The function has a boolean approximate parameter. If chosen True then you will get the approximate python implementation above. Otherwise, you get the precise but slower implementation that actually computes the Gauss error function (erf) of x element-wise.

An example building a Keras neural network with GELU activation function can be seen below. Notice that you can impose gelu as the activation of a layer either by using the alias ‘gelu’ or passing the imported gelu module directly. The fitting procedure is then similar to every other Keras network.

input_shape = (28, 28, 1)
num_classes = 10
gelu_act = gelu(approximate = False)
model = keras.Sequential(
    [
        keras.Input(shape=input_shape),
        layers.Conv2D(32, kernel_size=(3, 3), activation="gelu"),
        layers.MaxPooling2D(pool_size=(2, 2)),
        layers.Conv2D(64, kernel_size=(3, 3), activation=gelu),
        layers.MaxPooling2D(pool_size=(2, 2)),
        layers.Flatten(),
        layers.Dropout(0.5),
        layers.Dense(num_classes, activation="softmax"),
    ]
)

model.summary()

# Compile the GELU network
model.compile(loss="categorical_crossentropy", optimizer="adam", metrics=["accuracy"])

#Fit the GELU network 
model.fit(x_train, y_train, batch_size=batch_size, epochs=epochs, validation_split=0.1)

GELU in Torch

Similarly to Tensorflow, PyTorch offers GELU with both the approximate and precise form. You can access the function by importing the torch module and setting the approximate parameter to True if you want the faster implementation or leave the default value None for the precise form that computes the Gaussian Error Function. Inside the forward method you can use the gelu function and set the approximate parameter to True or not.

import torch.nn as nn 
import torch.nn.functional as F
import torch.optim as optim
import torchvision

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

def forward(self, x):
        out = self.conv1(x)
        out = F.max_pool2d(out, 2)
        out = F.gelu(out)        # Using exact GELU formula with erf 
        out = self.conv2(x)
        out = F.max_pool2d(out, 2)
        out = self.conv2_drop(out)
        out = F.gelu(out, approximate=True) # Using approximation
        out = F.dropout(out)
        out = self.fc2(x)
        return out

Conclusions

GELU activation function has seen a huge spike in its use during the last years. The advent of huge transformer models like BERT, GPT and other Vision Transformers (ViTs) beared the necessity for stronger regularization. GELU offers regularization hidden in the activation function, hence why it is being extensively used in models like BERT and GPT.

Coding GELU is very easy and the major frameworks support it by default in their activation functions modules.

REFERENCES

[1] Gaussian Error Linear Units (GELUs)

[2] GELU, the ReLU Successor? Gaussian Error Linear Unit Explained

[3] BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding

[4] tf.keras.activations.gelu

[5] torch.nn.functional.gelu

I hope you enjoyed this article and learnt something useful. If this is the case, then consider sharing this tutorial. In case you want to read more of my articles and tutorials, then follow me to get updated.

Thanks for reading, feel free to reach out!

My Links: Medium | LinkedIn | GitHub

---

GELU : Gaussian Error Linear Unit Code (Python, TF, Torch) was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI