Decision Tree Splitting: Entropy vs. Misclassification Error

Author(s): Poojatambe

Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.

Why is entropy preferred over misclassification error to perform decision tree splitting?

The decision tree uses a top-down, greedy search approach with recursive partitioning. In the decision tree, the goal is to partition regions recursively until homogeneous clusters are formed. To make these partitions, a sufficient number of questions are asked.

To split the tree at each step, we need to choose the best attribute that maximizes the decrease in loss from parent to children node. Hence, defining a suitable loss function is an important step.

Here, we will try to understand the entropy and misclassification error. Also, answer why misclassification error is not used for splitting.

Entropy

Entropy is the phenomenon of information theory used to calculate uncertainty or impurity in information. ID3 tree algorithm uses entropy and information gain as loss functions to choose data splitting attributes at each step.

Consider a dataset with C classes. The cross-entropy for region R is calculated as follows:

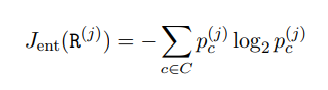
Where Pc= Proportion of randomly selected examples in class c.

The entropy ranges between 0 to 1. The zero value of entropy indicates the data is pure or homogeneous.

Misclassification error

The misclassification loss computes the fraction of misclassified samples. Hence, it considers major class proportion in region R. Consider C target classes. Let Pc be the proportion of samples of class c belonging to the C target classes.

The misclassification loss is computed as follows:

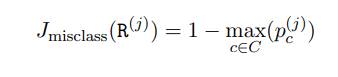
The misclassification error ranges between 0 to 0.5.

Entropy vs Misclassification Error

The maximum decrease in loss from the parent region to children nodes or minimize children loss is used to decide the attribute for the splitting of a tree. This decrease is called information gain given as follows:

To calculate loss, we need to define a suitable loss function. Let’s compare entropy and misclassification loss with the help of an example.

Consider 900 “positive” samples and 100 “negative” samples. Let’s assume the X1 attribute is used for splitting at the parent node. Consider the following decision tree with unequal distribution of data samples after splitting.

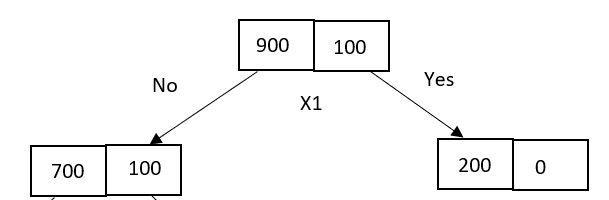
It has one pure node classified as 200 “positive” samples and an impure node with 700 “positive” and 100 “negative” samples.

With entropy as a loss function, parent loss is 0.467, and children loss is 0.544. As one node is pure, the entropy is zero, and the impure node has a non-zero entropy value.

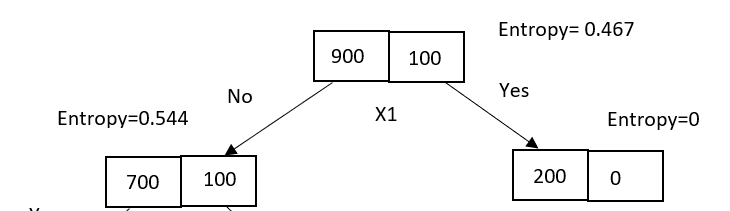
Using the information gain formula, the loss reduction from parent to children region is calculated as,

Gain = Entropy(parent) — [Entropy(left child)*(No of samples in left child/No of samples in parent) + Entropy(right child)*(No of samples in right child/No of samples in parent)]

Gain = 0.467 –[0.544*(800/1000) + 0 *(200/1000)]

Gain = 0.0318

With a misclassification error, parent loss is 0.1, and children loss is 0.125.

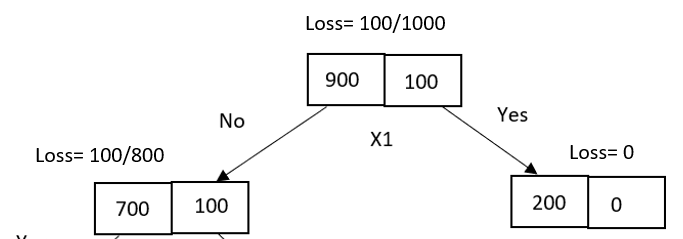
The information gain is calculated as,

Gain = ME(parent) — [ME(left child)*(No of samples in left child/No of samples in the parent) + ME(right child)*(No of samples in right child/No of samples in the parent)]

Gain = (100/1000) — [(100/800)*(800/1000) + 0*(200/1000)]

Gain =0

From the above gain values, we can say that as the misclassification error has not gained any information hence, further splitting of the tree is not required, and the decision tree is stopped growing. But in the case of entropy, the decision tree can be partitioned further until the leaf node is reached and the entropy value becomes zero.

Let’s prove this with a geometrical perspective.

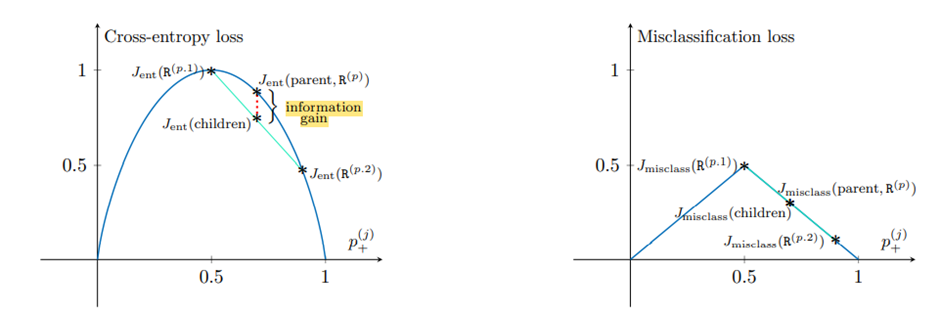
The above graphs are plotted with the assumption of an even split of data into two nodes. The cross-entropy function has concave nature that proves the loss of children is always less than that of the parent. But this is not the case with the misclassification error. Hence the children and parent loss are equal.

Therefore, compared to entropy, the misclassification loss is not sensitive to changes in the class probabilities, due to which entropy is often used in building the decision tree for classification.

The Gini impurity has the same nature as entropy which is also preferred for decision tree building over misclassification loss.

References

• https://tushaargvs.github.io/assets/teaching/dt-notes-2020.pdf
• https://sebastianraschka.com/faq/docs/decisiontree-error-vs-entropy.html

Check my previous stories,

1. Image Classifier with Streamlit

2. Everything about Focal Loss

Happy Learning!!

---

Decision Tree Splitting: Entropy vs. Misclassification Error was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.

Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI