Cosine Similarity for 1 Trillion Pairs of Vectors

Author(s): Rodrigo Agundez

Originally published on Towards AI.

Introducing ChunkDot

UPDATE
ChunkDot now supports sparse embeddings, you can read more about it here.

Bulk Similarity Calculations for Sparse Embeddings

ChunkDot support for sparse matrices

pub.towardsai.net

Success! I managed to find vector representations for my 1 million items… I just need to calculate the cosine similarity between all pairs to find the 20 most similar items per item. Then, from sklearn.metrics.pairwise import cosine_similarity, throw my 1 million vectorized items into it, and bam!
My computer explodes with a MemoryError or the kernel of my Jupyter notebook dies. The issue, I just tried to hold 1 Trillion (10¹²) values in memory (~8000 GB¹). Good luck!

This blog post introduces ChunkDot, a Python package I built to solve this problem. ChunkDot can do this calculation in ~2 hours while keeping the memory consumption under 20 GB, as shown below.

If you would like to skip the explanation and jump directly into the usage instructions:

chunkdot

Multi-threaded matrix multiplication and cosine similarity calculations. Appropriate for the calculation of the K most…

pypi.org

Motivation

The first time I encountered this problem was ~6 years ago while working for a client on an entity-matching use case. I was trying to match millions of records saved as free text to create golden records with the aggregated information from similar records². Back then, Spark was a new and very shiny tool, so I solved it using Spark, with some broadcasting and some C++ code wrapped in Cython wrapped in a UDF. I remember feeling that there might be a more elegant and simple way to solve this problem. I finally had time to look into it.

Since then, I have seen this issue pop up in one-to-many use cases. The idea of having items as vector representations and then trying to find the K most similar or dissimilar items per item appears in numerous use cases in Machine Learning. Some of these use cases are:

• Similar product recommendations.
• Name and Entity matching.
• Forecasting cold-start problem.
• Recommendation systems cold-start problem.
• User segmentation.

ChunkDot

The core of the problem is that the number of calculations scales with the square of the number of items. If we have N items, then the number of item pairs scales as N².
There is a silver lining, though, we only need the K most similar items per item. To determine which are the most similar K, we need to calculate all similarity pairs, but what if we do the calculation in batches (or chunks)? Keep the K most similar items for each batch, discard the rest, and then continue with the next batch until we have processed all items. This is the idea behind ChunkDot.

Let’s go over an example, suppose I have 10⁶ items, and I only require the top 100 most similar items per item. Then the number of similarity values I need is not 10¹² but 10⁶ x 100 = 10⁸, a reduction of 99.99%.³ This does not mean that the memory consumption will be reduced by 99.99%. It means the memory is no longer set by the output matrix but by the memory consumption of the algorithm itself.

Cosine Similarity Top K

Let’s go over how ChunkDot works. Even though the core of the implementation is in chunkdot._chunkdot, I’ll focus on the chunkdot.cosine_similarity_top_k function as shown below.

The algorithm consists of 3 parts, splitting the embeddings matrix into the optimal number of chunks, performing the parallelized operations over the chunks, and collecting the data from each parallel thread to form the similarity matrix.

Splitting the input embeddings into chunks

The first part of the algorithm receives as input a matrix of embeddings where each row is the vector representation of an item. Then it calculates the optimal chunk size to use during the parallelization. The optimal chunk size is the maximum number of rows to process per thread without exceeding the given maximum memory to use. If no maximum memory to use is given, then the system’s available memory is used. In parallel, an optional L2 normalization of the rows can be done. Finally, the normalized embeddings matrix gets split into pieces where each piece contains the number of rows equal to the chunk size. Now the data is ready to be parallelized.

Divide and conquer

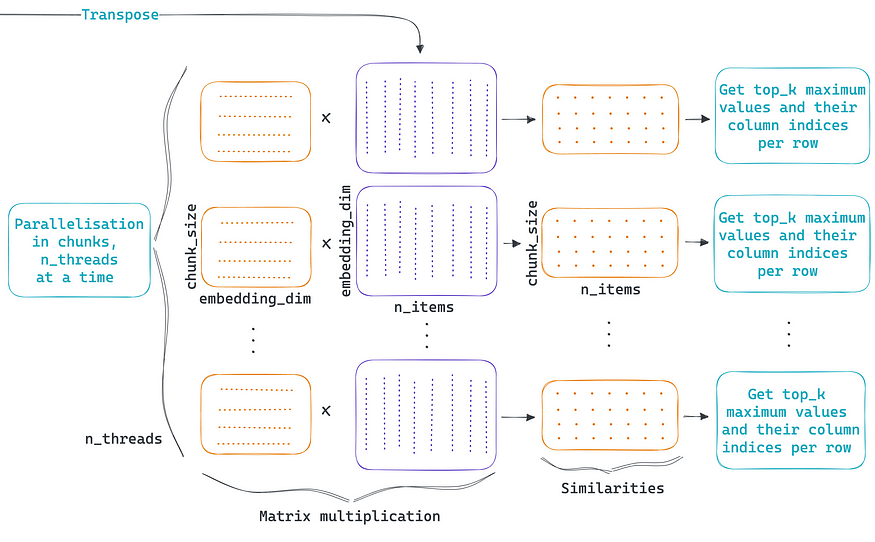
The second part of the algorithm performs all the parallel computations; each parallel thread calculates the cosine similarity between the chunk of items vs. all the items. As shown in the figure above, matrix multiplication is sufficient since rows are L2 normalized. Then, only the indices and values of the K most similar items are retrieved so that the density matrix is garbage collected to free up memory.

There is no free lunch; the price to pay for the parallelization and memory footprint reduction is that instead of having one big matrix multiplication, we have thousands of smaller ones plus the overhead of parallelization. This added complexity can raise the execution time to a non-usable level in practice. To manage the parallelization overhead efficiently and to perform these calculations as fast as possible ChunkDot uses Numba.

“Numba generates optimized machine code from pure Python code using the LLVM compiler infrastructure. With a few simple annotations, array-oriented and math-heavy Python code can be just-in-time optimized to performance similar as C, C++ and Fortran, without having to switch languages or Python interpreters.”

To take the most out of Numba, the code to optimize needs to be supported in no-python mode. At the moment of this writing, the numpy.argpartition function is not supported, which is why there is a numba_argpartition.py file in ChunkDot’s source code. I submitted this implementation to Numba via the PR below, which has been merged. The support should become native on Numba’s next release.

Add numpy argpartition function support by rragundez · Pull Request #8732 · numba/numba

Add numpy argpartition function support. I used some of the implementation of partition. Something to note it that I…

github.com

After the cosine similarity calculations and the retrieval of the K most similar items, we can collect all the values and indices to construct the final sparse similarity matrix.

Similarities as a CSR sparse matrix

The third part of the algorithm consists of creating the sparse similarity matrix containing the K most similar items per item. This will be a sparse matrix of dimensions n_items x n_items containing only n_items x top_k non-zero values. The final output will the returned as a SciPy CSR sparse matrix.

Chunk size calculation

The idea behind calculating the biggest possible chunk size is that the bigger the chunk, the fewer threads are needed, therefore reducing the execution time of the algorithm.
To reduce memory utilization, all threads outputs are collected in arrays that are passed by reference to each thread. ChunkDot’s algorithm memory consumption is then described by⁴:

Where the number of threads is given by Numba’s get_num_threads function. The optimal chunk size is the solution for chunk_size in the equation above.

Memory and speed

I made a benchmark comparison with SciKit-Learn’s cosine similarity on memory consumption and execution time.

This is not entirely a fair comparison since the purpose of SciKit-Learn’s cosine similarity function is to retrieve the similarities of all pairs of items and not just the K most similar. Having said that, I do not know of any other similar and simple approach that can be executed on a common laptop without a rigorous setup. I also think most of us will be looking first at the SciKit-Learn function to solve this problem. Therefore it seemed appropriate to benchmark against it.

The figure below shows the results. For the SciKit-Learn implementation, I did not go above 50K items as it was already taking ~20 GB of memory. I did include a projection of the expected memory consumption.

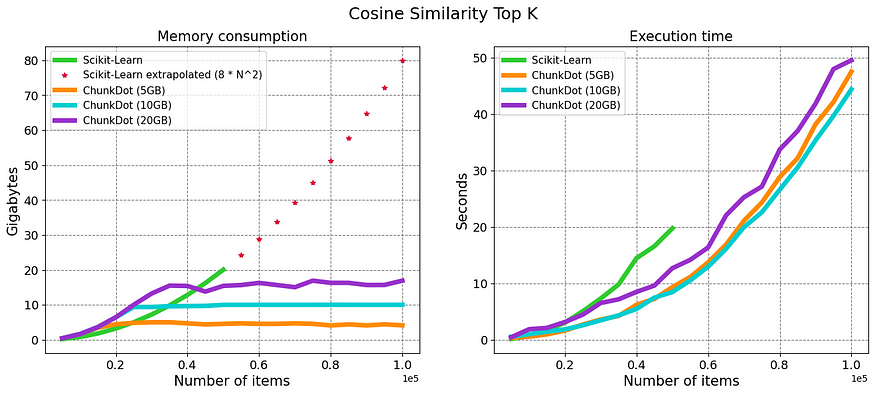
The results show that the algorithm works, it can do the calculation for a large number of items while keeping the memory consumption capped. In the above-left figure, SciKit-Learn’s implementation is compared with ChunkDot using 3 different maximum memories: 5 GB, 10 GB, and 20 GB.

Nowadays is common to have 20 GB of RAM; you can easily compute 100K different items and retrieve their K most similar items in around 1min.
Quite unexpectedly, the ChunkDot algorithm is also faster, thanks, Numba! and it seems that the maximum memory to use does not matter that much for execution time… weird.
I did a thorough review of the results and methodology and reran them several times, but I wouldn’t claim that ChunkDot is univocally faster. What I do know for certain is that I was able to do the calculation for 100K and 1 million items without a problem.
For 1 million items, which are 1 trillion comparisons, I only had to wait ~2 hours using 20 GB of memory, as shown in the figure below.

Usage

pip install -U chunkdot

Calculate the 50 most similar and dissimilar items for 100K items.

import numpy as np
from chunkdot import cosine_similarity_top_k

embeddings = np.random.randn(100000, 256)
# using all you system's memory
cosine_similarity_top_k(embeddings, top_k=50)
# most dissimilar items using 20 GB
cosine_similarity_top_k(embeddings, top_k=-50, max_memory=20E9)

<100000x100000 sparse matrix of type '<class 'numpy.float64'>'
 with 5000000 stored elements in Compressed Sparse Row format>

Conclusion

I hope you find this blog post and ChunkDot useful! I enjoyed a lot working on this problem and getting satisfactory results. Some potential improvements:

• Add support for input embeddings as a sparse matrix. This might already be supported, but I just haven’t thoroughly unit tested for this. I decided to return a TypeError exception to avoid silent errors. This will especially enable NLP use cases where the vectorization of items is done using n-grams, bag-of-words, or similar.

UPDATE. ChunkDot now supports sparse embeddings, you can read more about it here.

Bulk Similarity Calculations for Sparse Embeddings

ChunkDot support for sparse matrices

pub.towardsai.net

• The cosine similarity between item i and j, is equal to the similarity between j and i. It is enough to perform the calculations that render the upper-triangular matrix. This can be done via the Einstein summation function in Numpy, unfortunately, is not supported by Numba at the moment.
• Instead of returning the K most similar items, return items whose similarity is above/below a certain threshold.
• Add GPU support since Numba supports it.

Numba for CUDA GPUs — Numba 0.56.4+0.g288a38bbd.dirty-py3.7-linux-x86_64.egg documentation

Callback into the Python Interpreter from within JIT’ed code

numba.readthedocs.io

[1] These calculations are normally returned as float64. Not that it matters, though, with float32 I would still need ~4000 GB of memory.

[2] The situation was a bit more complex, but this is the part related to this blog post.

[3] Here I have ignored the memory contribution from storing the indexes needed to assign each similarity value to an item pair. Their memory contribution, though, is irrelevant to this conclusion.

[4] Supposing that all threads could be holding the maximum amount of memory at the same time.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI