
Building and Optimizing Randomized Complete Block Designs using SAS
Last Updated on February 27, 2022 by Editorial Team
Author(s): Dr. Marc Jacobs
Originally published on Towards AI the World’s Leading AI and Technology News and Media Company. If you are building an AI-related product or service, we invite you to consider becoming an AI sponsor. At Towards AI, we help scale AI and technology startups. Let us help you unleash your technology to the masses.
Statistics
In the animal sciences, the design that is used the most is the Randomized Complete Block Design (RCBD). This design can be compared to the stratified-randomized design often used in the life sciences. Its ingenuity lies in using the design of an experiment to include variance in order to exclude variance. That is correct. We include variance in our design to make sure we can control it, so when the time comes to analyze the data we can exclude it. I have written about randomization and blocking in a previous introductory post. In this post, I will dive deeper into the RCBD.
The RCBD is a combination of building blocks and randomization. There really is nothing more to it.

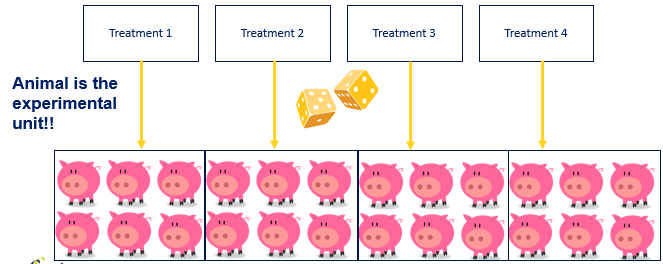
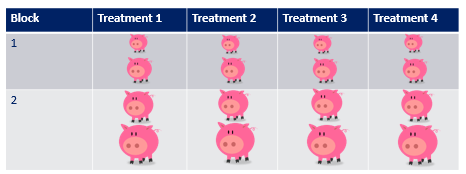
Now, let's say that our pigs are not all of the same colors. If we would just randomize the pigs, we would have an uneven distribution of color within our treatments. The color of the pig could be a covariate we need to deal with in our analysis. Although this is really fine, it is much more efficient and effective to just deal with a potential confounder in the design stage.
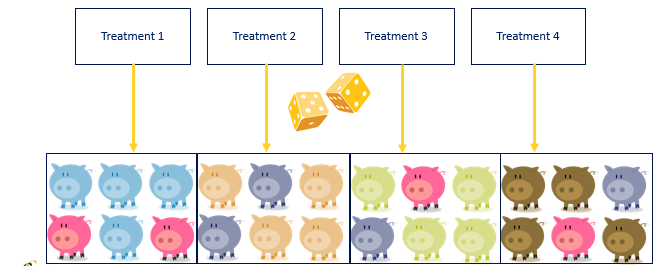
A complete randomized design is a design of large numbers. It assumes that, by randomizing from a population, the samples representing each treatment will be equal on all characteristics, except the treatment → comparison will be pure. In animal science, this will rarely be the case because we cannot implement the numbers needed to reach this level of purity. However, we do have two alternatives:
- Include color as a covariate in the model
- Include color in the design → Randomized Complete Block Design
We will now show how an RCBD design works in practice. First, we create blocks, and we create just as many blocks as there are colors. Often, such a one-to-one relationship is not possible and you need to create blocks that have very little within-block variance and a lot of between-block variances.
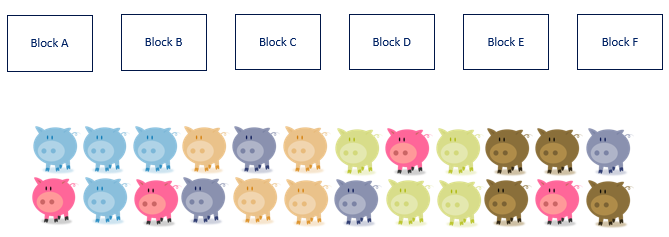
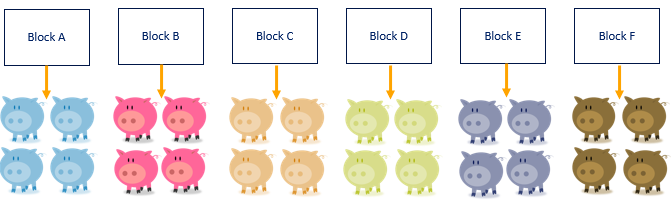
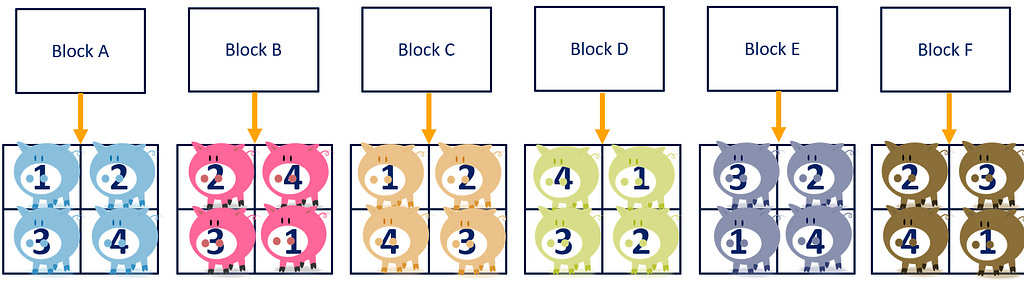
A Randomized Complete Block Design actually means ONE replicate per treatment*block combination. This will lead to the example below.
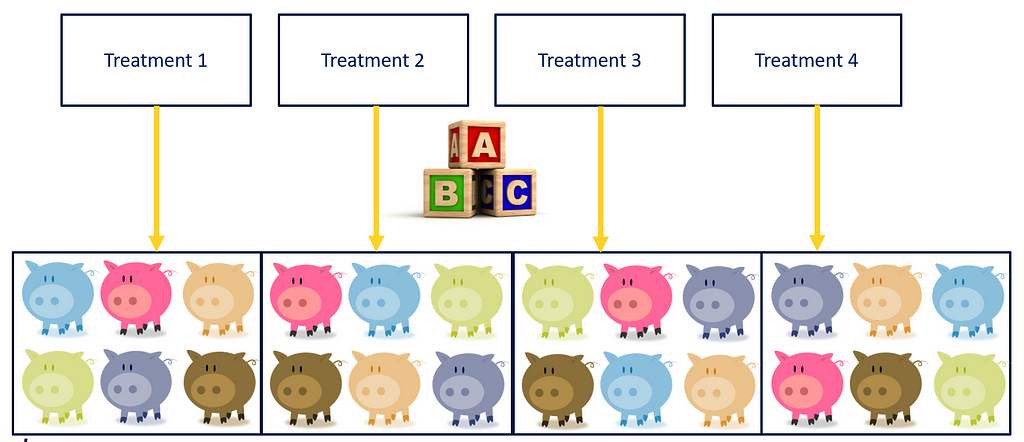
As a result of the blocking, each treatment now has a similar distribution with regards to the blocking factor → COLOR. Here, block represented the color of the pigs, and by blocking we made sure that each treatment has at least one pig of each color. However, we rarely have such nice predefined levels of a blocking factor. In addition, to get a good estimate of the variance attributable by the blocking factor, we need more than two levels of each block, which can be difficult to accomplish
In summary, a Randomized Complete Block Design ensures that:
- randomized treatments are randomized within a block
- all treatments are in one block
- there is one replicate per block*treatment
- each block is a mini-experiment since we compare treatments within each block.
In general, an RCBD is more efficient than a Completely Randomized Design (CRD) since units within blocks are more similar (homogenous) than units between blocks (heterogeneous). Hence, after accounting for the block variation, the experimental error becomes smaller
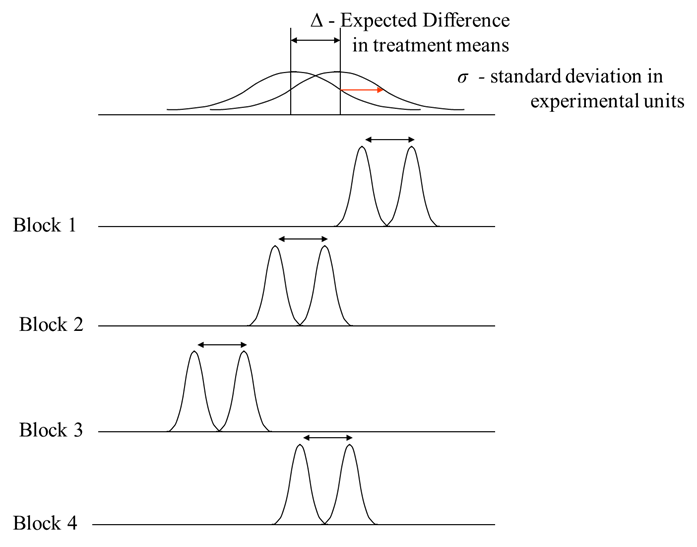
The graph above shows that the variance in each treatment has been partitioned into blocks. Each block is a mini-experiment with its own treatment difference and specific variance. This design increases the signal-to-noise ratio as the treatment differences across the blocks are similar
The biggest question that comes to mind is WHEN blocking is actually helpful. As you might have guessed, its helpfulness is dependent on its ability to capture variance. The more variance, the better.

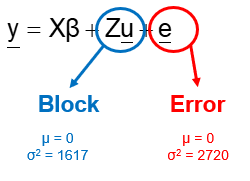
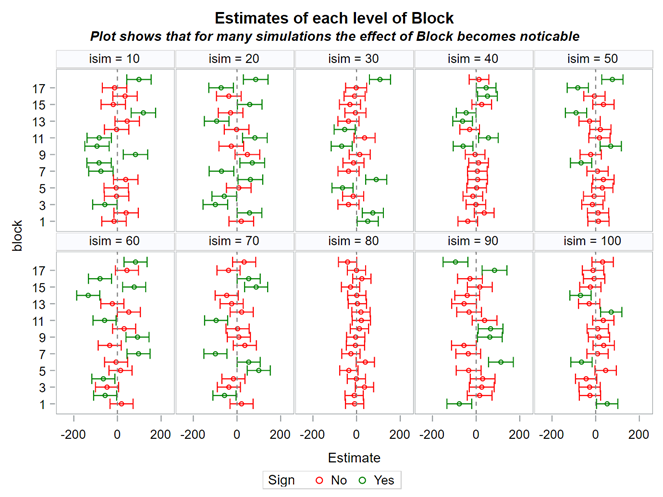
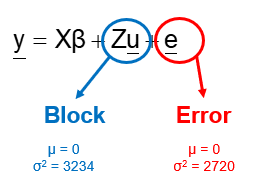
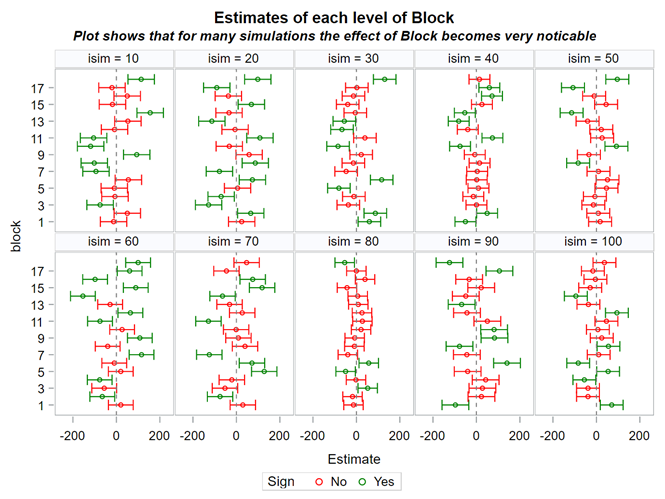
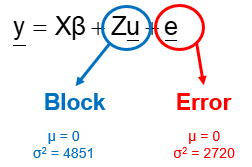
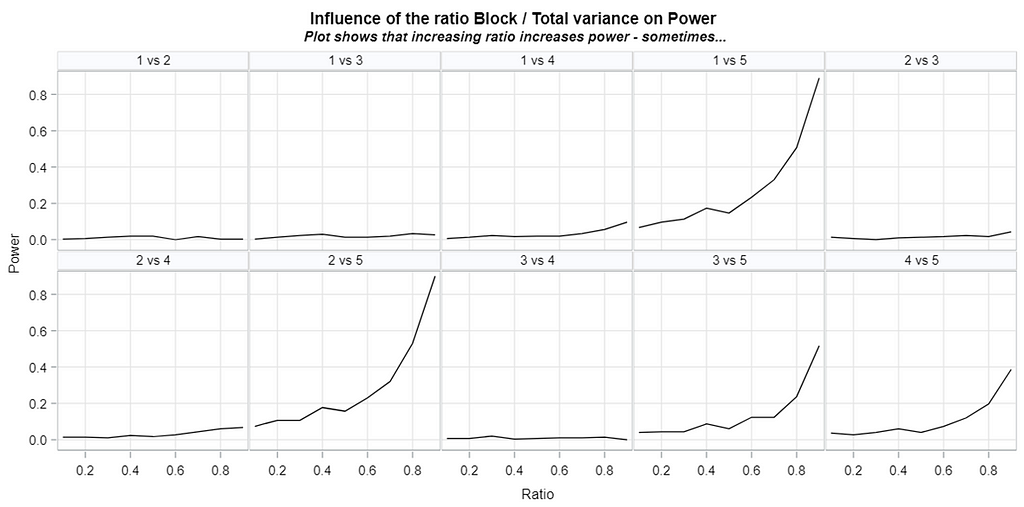
Blocking is all about explaining the variation YOU created. If your blocks don’t capture variation it is useless to design a blocked study and can even be harmful to your power. To decide if blocking is helpful you need to ask yourself:
- What is my main outcome of interest?
- Are there sources of variation that will decrease my signal-to-noise ratio
- How large will this decrease be?
- Will a randomized block design help me to limit the decrease?
- Will a randomized block design help me to actually increase the signal-to-noise ratio?
In an optimal Randomized Complete Block Design, you have:
- Homogeneity within the block
- Heterogeneity across the blocks
If the blocks are too large, or there are too few blocks, the blocks will be too variable and thus unable to efficiently catch and delete variance


The more variance a blocking structure can capture, the fewer blocks you need to capture the ‘true’ variance within a single study. As with sample size, it is better to have more blocks than fewer. In the end, it depends on the ability of the blocks to create a between-block variance.
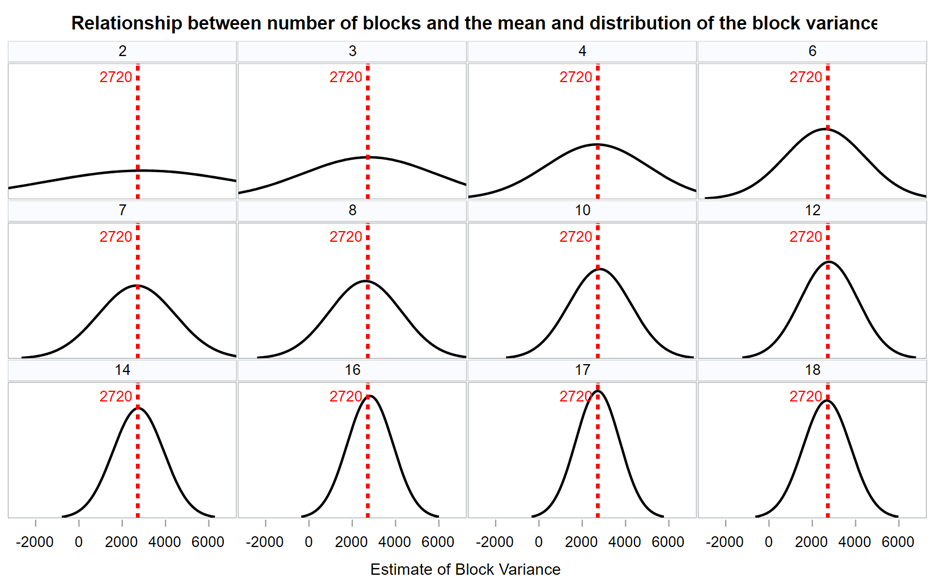
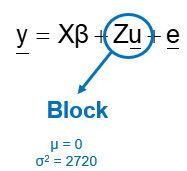
Now, what if you design an RCBD but analyze it as a CRD? By doing so, you fail to capture the variance attributable by block. This variance will go in the garbage can — experimental error — and you will decrease the signal-to-noise ratio → treatment effect / experimental error. In addition, you will increase your chance of finding a type II error because there is a less true experimental error than indicated by the model
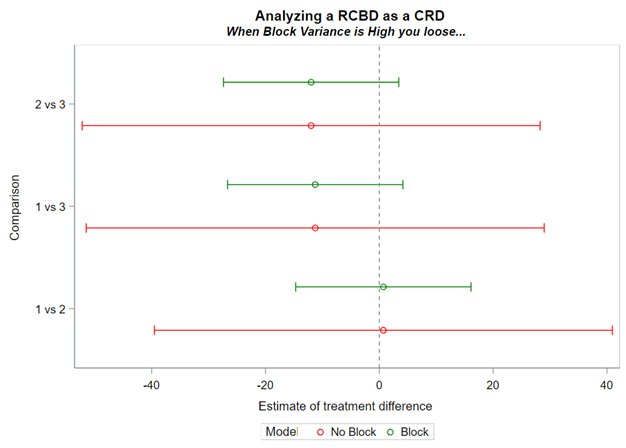
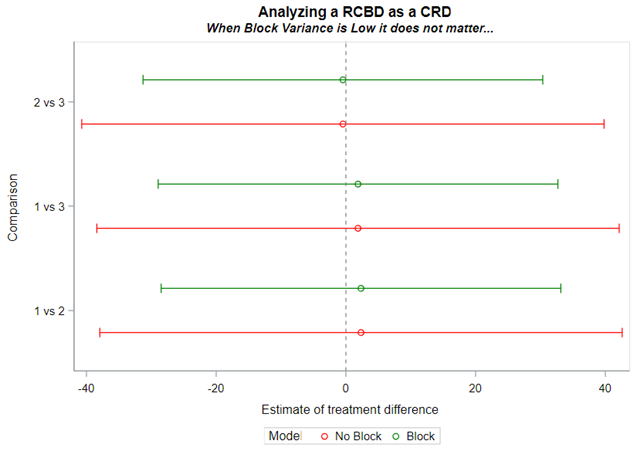
Blocking is like signing a contract. Once you are in, you are in and these blocks are a useful — and often necessary — tool depending on your research objective. Like with everything in a design, blocks have to be properly designed and accounted for in the statistical model. For instance, if an interaction between the outcome variable and the initial bodyweight of the animal is not expected, a Complete Randomized Design may do the job just fine. Here, initial body weight is a quantity and can be used as a covariate
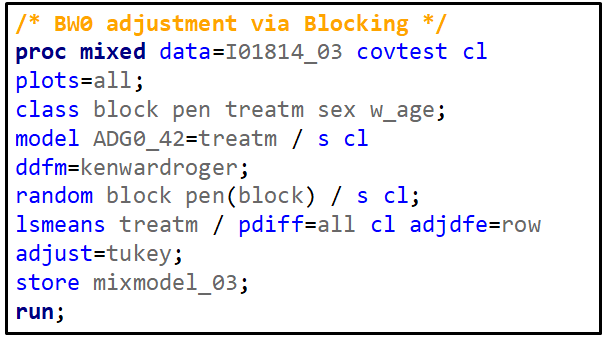
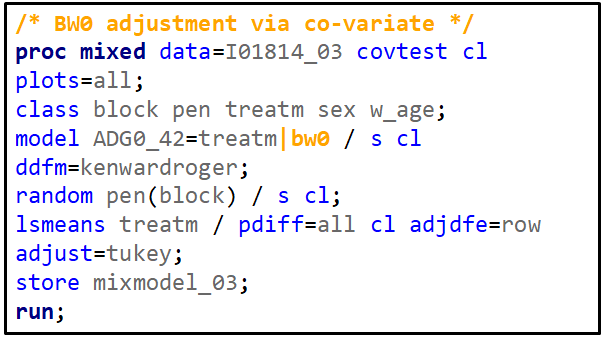
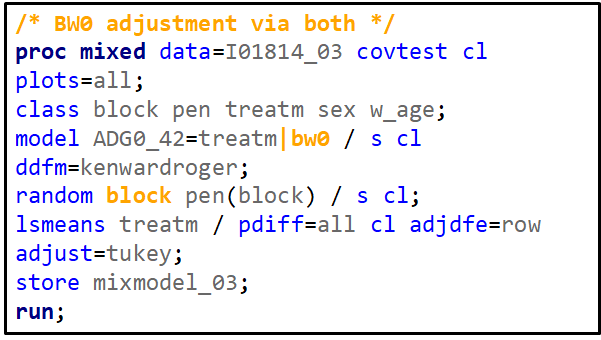
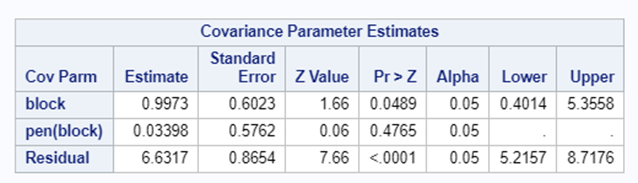
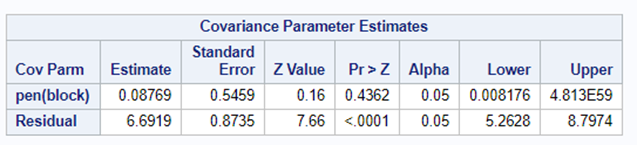
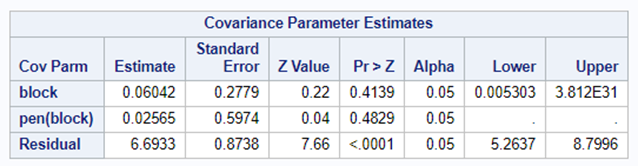
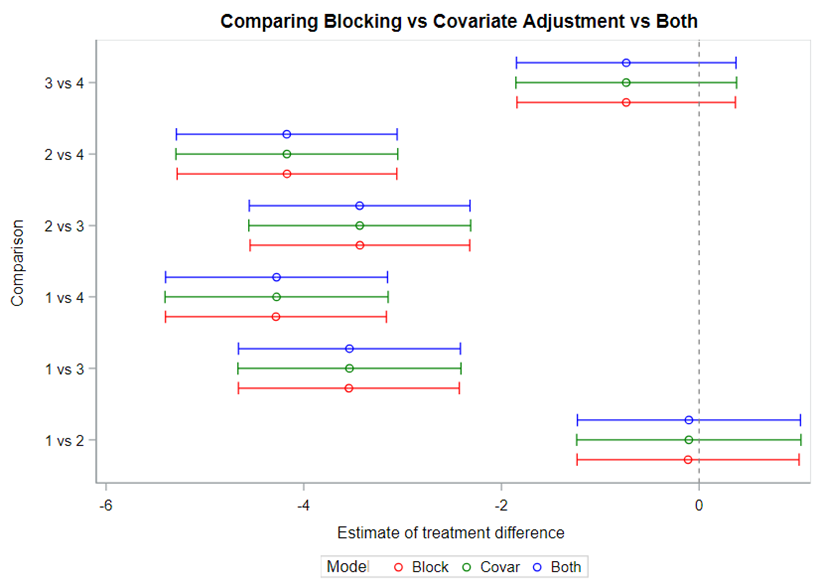
Blocking works best if it represents the true population. However, if you have more interest in a specific part of the population, or you expect more variance in a specific part, it might be useful to include more blocks of this part
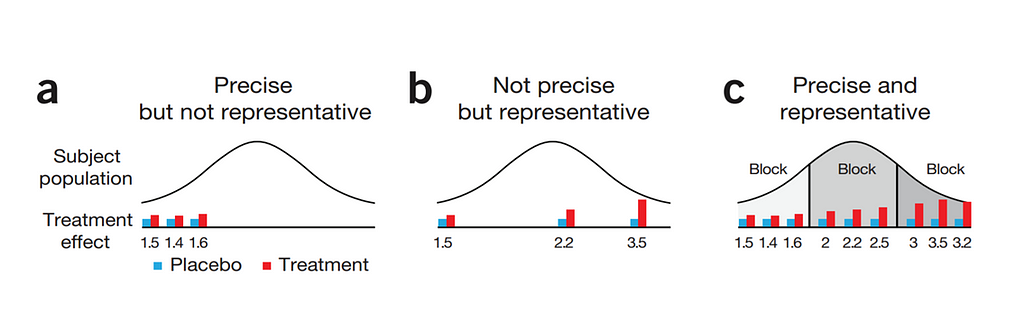
Now, what if more studies start with animals from the same population Sometimes multiple experiments start with animals from the same pool. The allotment of animals to the different experiments can have a large impact on the outcome. In most cases, a solution is possible that works for all affected experiments. However, this is not always the case, which can be seen in the graph below. Here, a single large animal pile was used to feed two separate studies. The allotment of the performance study influenced the allotment of the preference study.
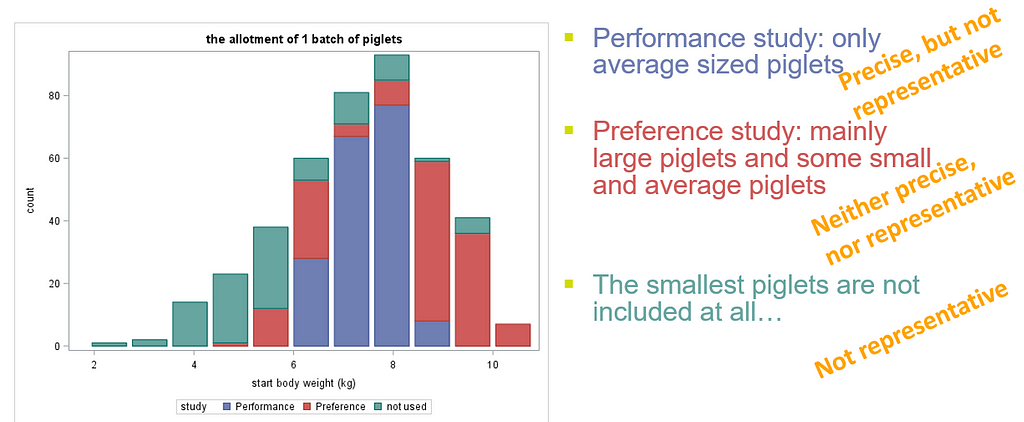
All piglets, but the very smallest, are allotted randomly to the studies. Both studies are representative. However, especially the performance study is less precise. The number of replicates is the same, but the variance increases. The will have a negative effect on the power of the study.
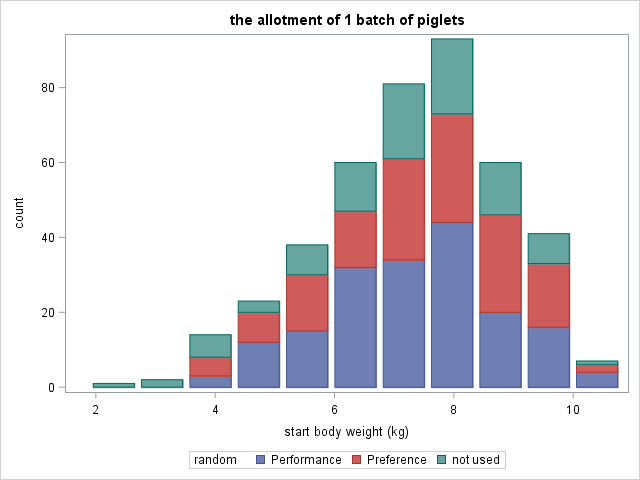
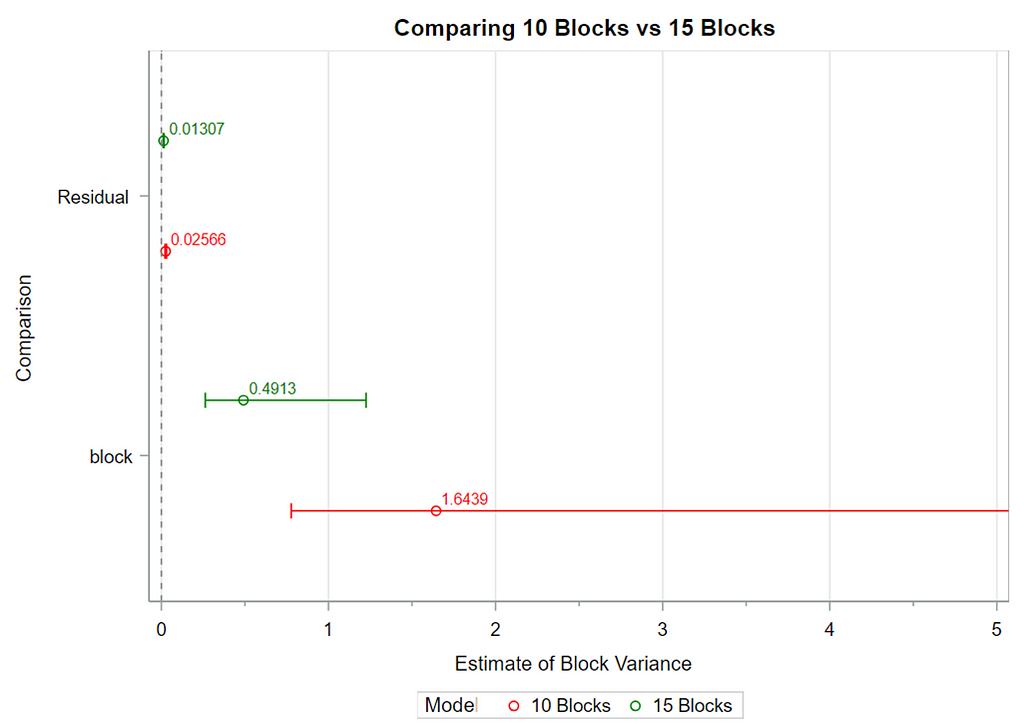
Now, we have discussed several times the importance of using a correct blocking strategy. The blocks need to be able to capture variance in such a way that the between-block-variance is maximized at the expense of the within-block variance. The way the blocks are set up is detrimental to this.
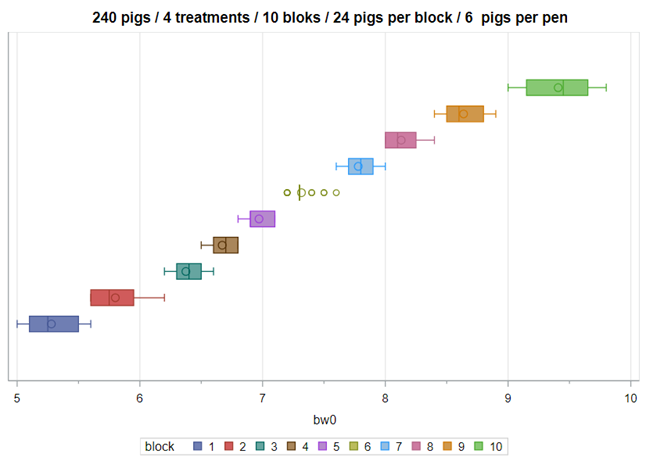
Below you see an actual blocking strategy to the left, using the body weight at day zero as the blocking parameter. On the right, you see a simulated blocking strategy, using the distribution of body weight at day zero to inform the size and thus the number of blocks. It does not take great foresight to ascertain which study will prove to have a better blocking strategy.
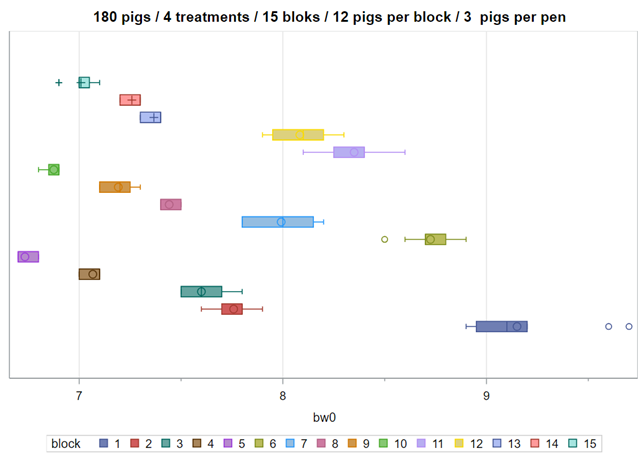
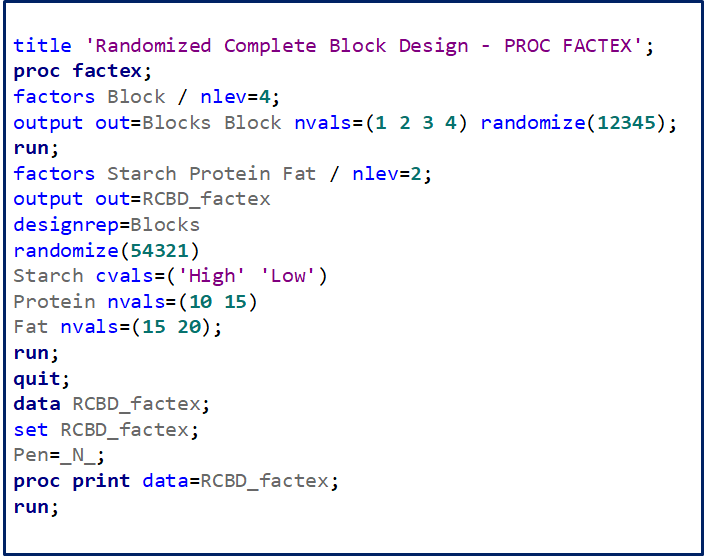
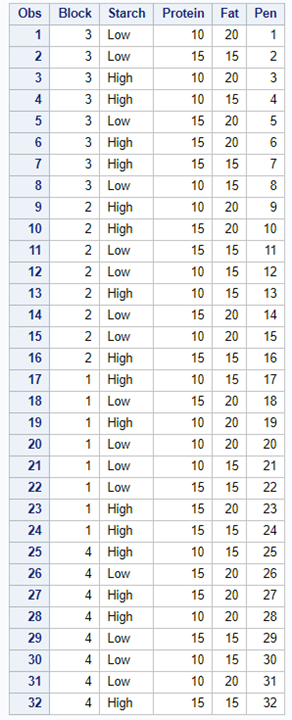
A Randomized Complete Block Design can easily be created and optimized using PROC FACTEX. Below, you see a 2³ full-factorial across four blocks leading to 32 experimental units. PROC PLAN can of course accommodate here as well.
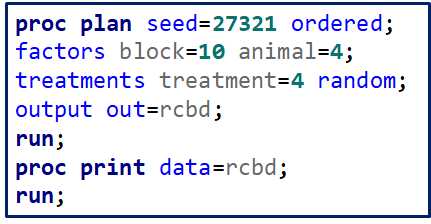
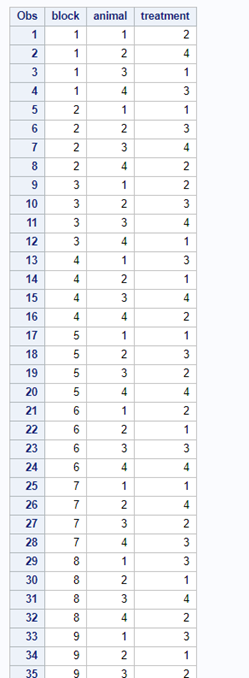
Then, there is always the data step way of building nested datasets. In SAS this is childsplay.

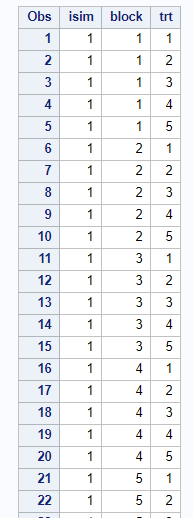
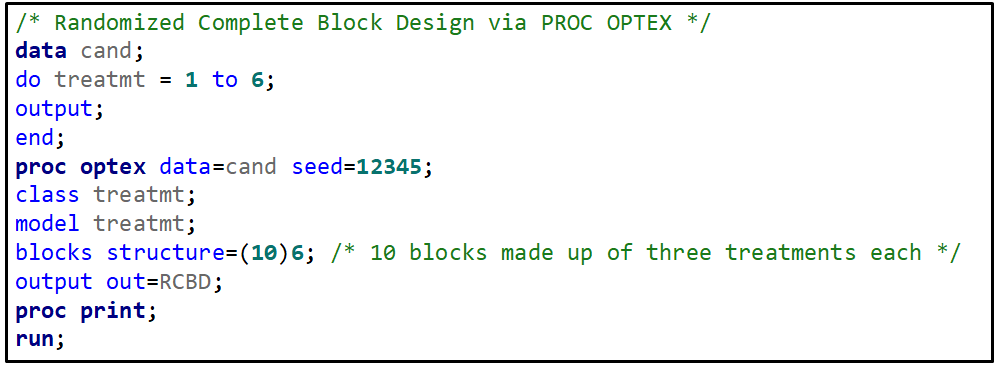
Last, but not least, we can use PROC OPTEX to build a RCBD.
Now, let's start analyzing an RCBD design. Below you see me trying to include a treatment*block interaction. Remember, an RCBD has a single replication per treatment*block interaction which means that including the treatment*block leaves no information to determine the residual variance. As you can clearly see.


If you want to analyze the interaction between treatment and block, you need to replicate the treatment within a block. However, this will make the blocks larger which could lead to less homogeneity within a block, so less homogeneity
Hence, a Randomized Complete Block Design is a great design if:
- there is enough variance to capture by blocking
- the blocks are set up in a way that they are homogenous within and heterogeneous between.
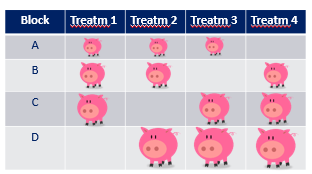
If you have many treatments, it could be quite difficult to obtain homogenous blocks, as you can see in the colored bar here.

Hence, this is where a Randomized Incomplete Block Design (RIBD) can be of great value as it keeps the blocks homogenous by not having all the treatments in each block. A distinction can be made between a balanced and partially balanced design.
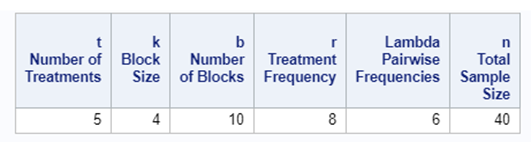
The RIBD has four key characteristics:
- Each treatment level is equally replicated
- Each treatment DOES NOT appear in each block
- Each treatment appears the same number of times over blocks
- Each pair of treatments appears in a block the same number of times
To build such a design, you need to address a build-in SAS macro and then use PROC OPTEX.


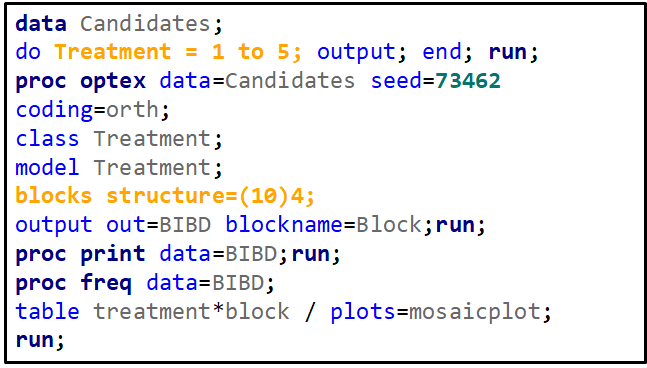

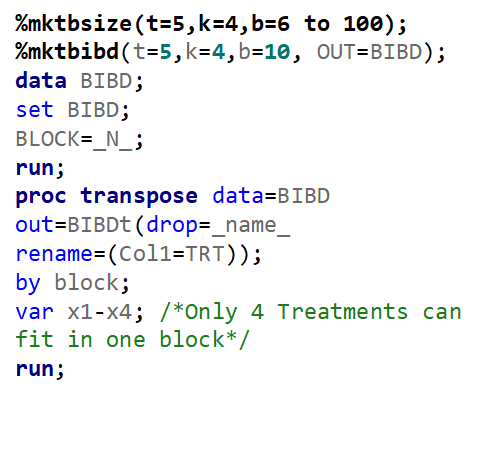
Of course, even though the Incomplete Block Design is balanced, it is no match for an RCBD. Nevertheless, if you do not have the room to accommodate the necessary sample size for an RCBD, I suppose the RIBD is the best way to go.
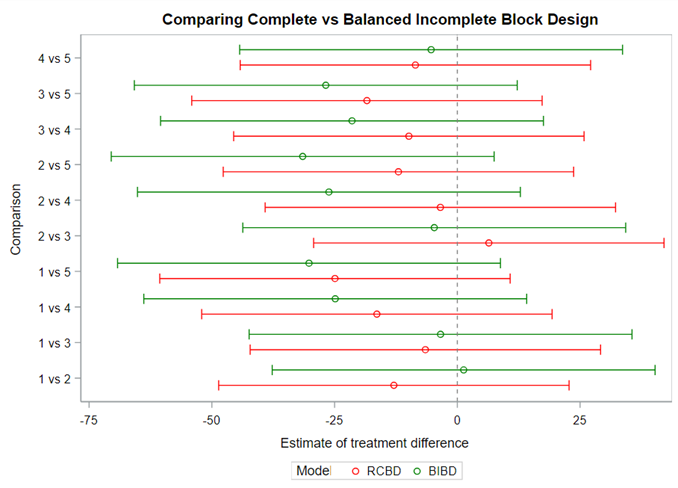
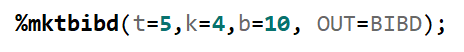
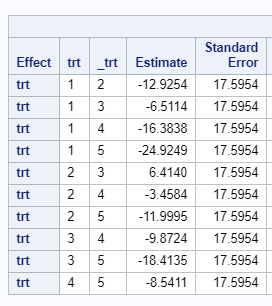
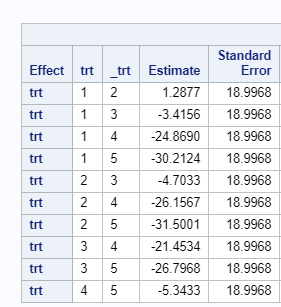
Since we have a fully balanced incomplete block design it is a bit of a no-brainer that we can also create partially balanced incomplete block designs. Here:
- each treatment does not appear in each block
- each treatment does not appear the same number of times over blocks
- each pair of treatments does not appear in a block the same number of times



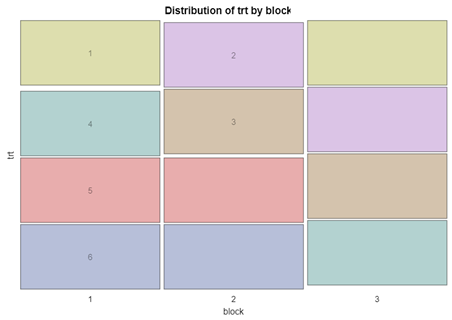

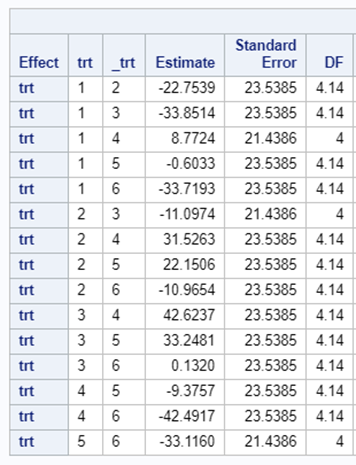
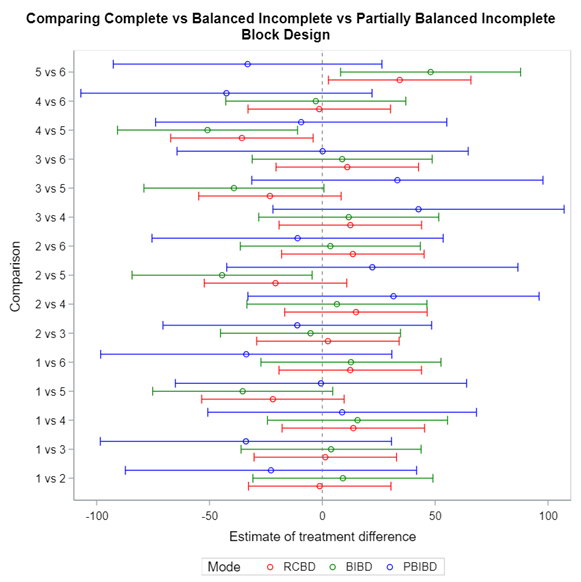
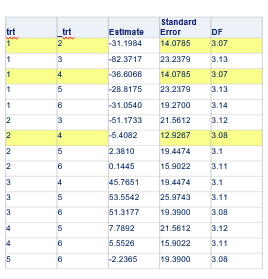
Let’s say I have six treatments, four blocks, three treatments per block and I am mostly interested in comparing 1 vs 2, 1 vs 4, and 2 vs 4. A simple start would be by using PROC PLAN.
Below, you see an example of designing an RCBD using multiple steps of PROC FACTEX to build nesting of fixed and random components, starting with block, adding treatment, and then adding sex as factors.

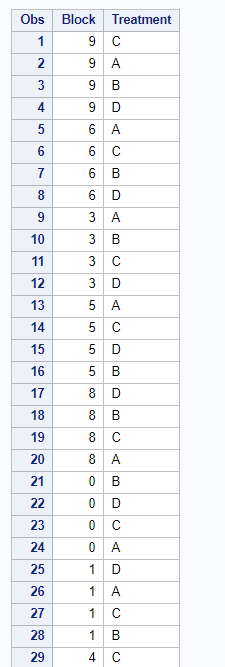
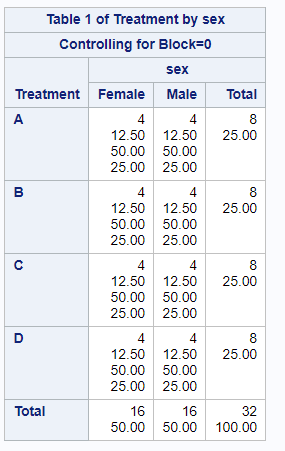
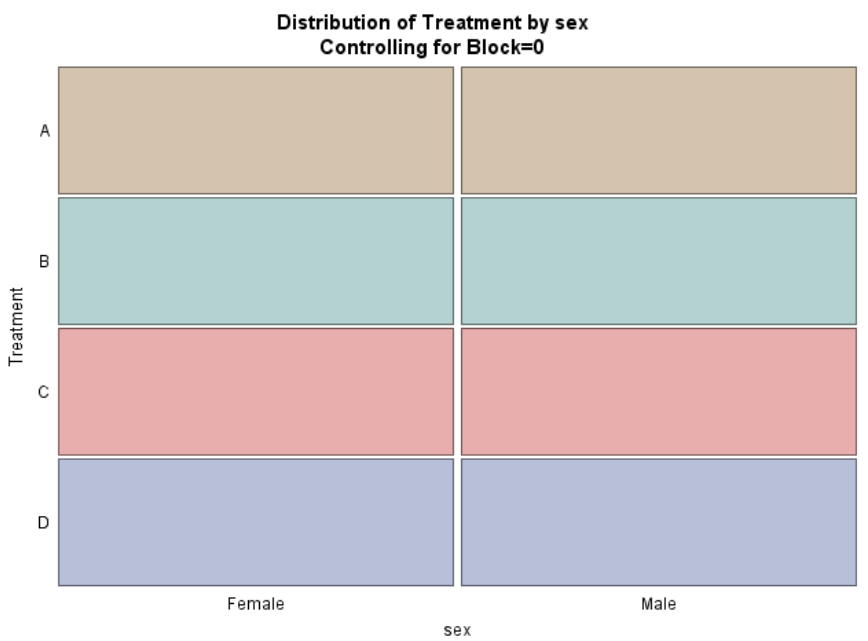
One can also easily ask SAS to transform full-factorial into an RCBD, of which you can see two examples below.

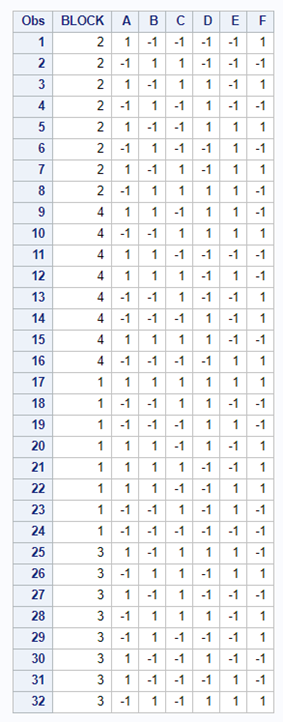

In summary, there are two major reasons for blocking a study: (1) practical, and (2) statistical.
PRACTICAL reasons for Blocking
- Conditions cannot be kept constant in the study.
- Divides experiment into mini-experiments with homogenous animals.
- The experiment is more manageable.
STATISTICAL reasons for blocking
- Control variance by creating and accounting for created variance.
- Cancel-out block-to-block variation
- Estimate treatment differences better → standard error only due to experimental error
Building and Optimizing Randomized Complete Block Designs using SAS was originally published in Towards AI on Medium, where people are continuing the conversation by highlighting and responding to this story.
Join thousands of data leaders on the AI newsletter. It’s free, we don’t spam, and we never share your email address. Keep up to date with the latest work in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.
Published via Towards AI














