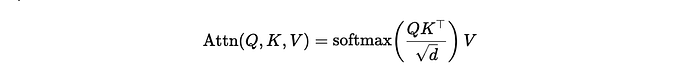
Approximate Nearest Neighbors

Author(s): Harshit Sharma

Originally published on Towards AI.

And where to find them using Product Quantization

You must have heard of KNN (k-Nearest Neighbors) and the fact that it is as easy as it gets when retrieving the most similar items to a user query.

But this simplicity of KNN hits hard when the number of training samples increases.

And this is because the complexity of KNN is:

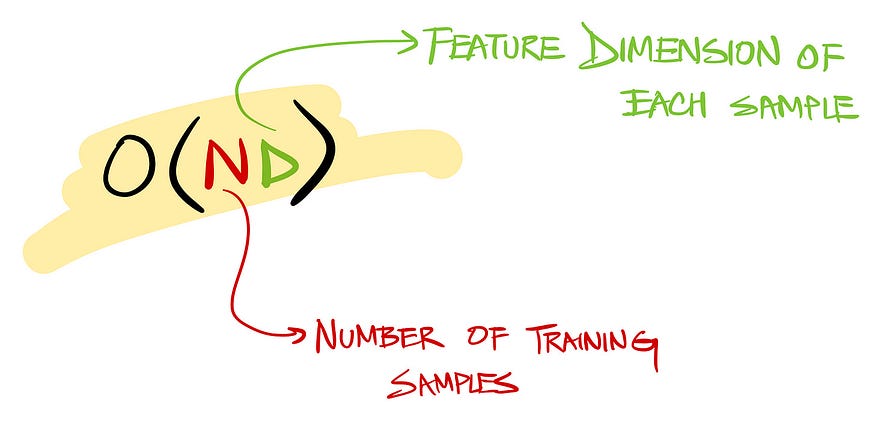
It’s linear in the number of samples and the feature dimensions of the training samples. It will cry in the face of billion+ data points.

Can we do better?

Yes, through a class of approaches known as

These approaches optimize the search process from two perspectives

1. Memory (required to store the vectors)
2. Speed (of search given a query vector)

Below is a mind map of various Approximate Nearest Neighbor search approaches.
And the one we will be going through in this short will be Product Quantization.

The idea is to represent the original vectors in a compressed format to occupy less space in the vector database, and also optimize the search complexity.

It’s a 3 step process:

Step1: Split vector into equally sized chunks — subvectors

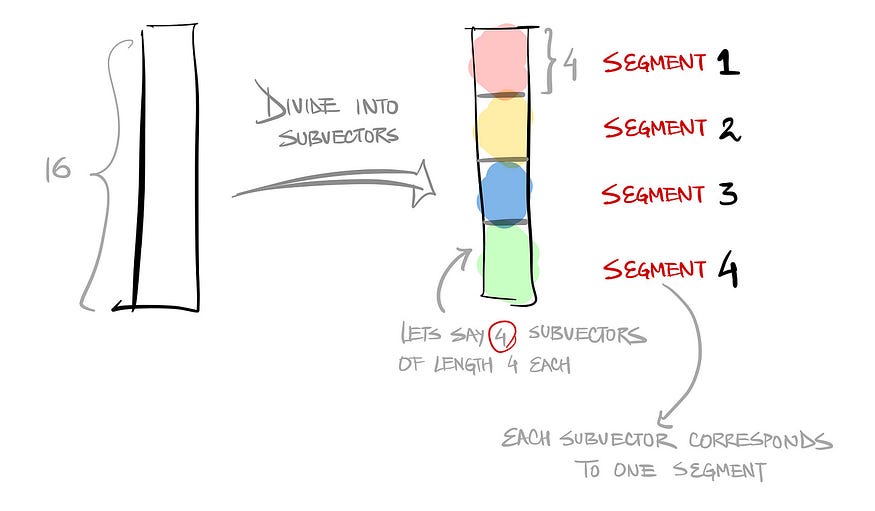
Each segment consists of “k” centroids trained using K-means from the training data (of that segment)

The training phase is shown below. All the vectors in the training data are segmented into the same number of subvectors. And all the subvectors corresponding to the same segment are collectively used to train a K-Means model to get the k centroids.

Step2: Assign each of these subvectors to its nearest centroid

Coming back to the example vector. Once the vector is segmented into different subvectors, each subvector is then assigned to the closest of the centroids of that segment.

Step3: Replace each of these centroid values with their unique IDs

Remember each of those centroids is actually vector of the same dimension as the subvector.

Once each of those subvectors is assigned a centroid, it’s time to replace those centroid vectors with their IDs. And those IDs in turn form a vector:

To summarize, we went from:

That’s a 16x reduction in the required memory. Initially, we had 32-bit floats in the original vector, but finally, they are stored as 8-bit integers in the vector database.

And this is how Product Quantization helps in optimizing the memory.

But how does this help in optimizing the search complexity?

Let’s answer that in the coming short (to be out soon)

Hope you enjoyed this quick read !!

Originally Published at Intuitive Shorts:

Follow Intuitive Shorts (a Free Substack newsletter), to read quick and intuitive summaries of ML/NLP/DS concepts.

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI