Inventory Optimization with Data Science: Hands-On Tutorial with Python

Author(s): Peyman Kor

Originally published on Towards AI.

Intro

Effective inventory management is important for businesses across various industries. In the previous blog, we explored how to model the process and how to frame it with the Markov Process.

The below illustration shows how to model the probabilistic movement of the states:

In this blog, we go one step ahead and think about how to frame inventory optimization with the Markov Reward Process (MRP). Here, we have the additional term “Reward,” meaning we need to think about how to assign “Reward“ to the process.

This blog will have the following structure:

• Markov Reward Process (MRP)
• Reward Modeling Bike Shop Inventory Optimization
• Hands-On Python Coding
• Bellman Equation
• Putting Everything Together
• Key Summary

At the end of the blog, you will learn:

• How to frame the Markov Reward Process (MRP) for Bike Shop Inventory Optimization.
• Write hands-on code to model MRP in Python.

Markov Reward Process:

Markov Reward Process (in short MRP) is a Markov Process, where the sequence of “Rewards, State” tuple follows the Markov Reward Property as:

Here, R_{t+1} is a reward induced if we move from state S_{t} to S_{t+1}.

MRP need a new Python data structure. The new data structure not only keeps state evolution with its probability, but this time it’s rewards too.

To show how MRP data structure looks like in Python, I am giving an example of MarkovRewProcess_Exa data structure. Let me explain what it looks like:

MarkovRewProcess_Exa = {"Current State A":{("NextS1fromA", "RewardS1fromA"):"PNextS1fromA",
 ("NextS2fromA", "RewardS2fromA"):"PNextS2fromA"},
 
 "Current State B":{("NextS1fromB", "RewardS1fromB"):"PNextS1fromB",
 ("NextS2fromB", "RewardS2fromB"):"PNextS2fromB"}}

The **MarkovRewProcess_Exa** is a dictionary where the keys are the current state, S_t. Then, each state going to a new state would have some rewards, and from state S_t to tuple of (S_{t+1}, R_{t+1}) has a specific probability.

Here you can see when you are at S_t = Current State A, and you move to next (state, reward) written as (“NextS1fromA”, “RewardS1fromA”), the probability of happening of this move is : **PNextS1fromA**:

MarkovRewProcess_Exa["Current State A"][("NextS1fromA", "RewardS1fromA")]

And we can iterate over all possible (new state, reward) to get the overview of the process evolves:

for (state, value) in MarkovRewProcess_Exa.items():
 
 print("The Current state is: {}".format(state))
 
 for (next_state,reward),trans_prob in value.items():
 
 print("The ({} with {}) \nwith Probability of: {} \
 ".format(next_state, reward, trans_prob ))p

Reward Modeling Bike Shop Inventory Optimization

Now, at this stage, we need to assign a reward to the Markov Process of Bike Shop, as we discussed in the previous article. What we mean is that given you are at state S_t, if you move to state S_{t+1}, how much “cost/reward” is accrued?

In the example of Bike Shop Inventory Optimization, the cost is compromised of two parts:

– 1) When we hold inventory items in the inventory, we are making the cost of overnight holding costs. Imagine holding items in inventory is costly (maintenance or other fees).

– 2) The second cost is missed customer cost. This happens when you have three bicycles in your inventory, but there are five customers. In this case, you missed two customers.

In other words, reward in the example of Bike Shop is defined as:

However, we can not write the equation straightforwardly, as we need to distinguish two different cases,

Case I) The number of available items in inventory meets the “demand”

In this case, we do not have any “Missed Customer cost”. Meaning only we are dealing with overnight holding costs. We assume this cost of overholding per bicycle (item) is equal to h. We can write that

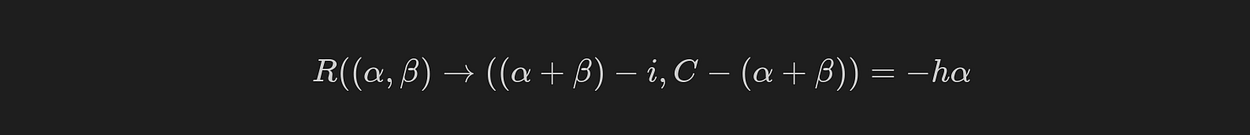
Note that states are “recorded” each day at 8 PM . For example, today is Monday, and at 8 PM, you record that you have two bicycles in the inventory (α = 2) and one bicycle order that arrives tomorrow morning at 6 AM (β = 1). If tomorrow's demand is i=1. Given this, the reward is the equal cost of holding:

-hα=-h×2

Case II) The number of available items in inventory is lower than the “demand”

In this case, when demand i is equal and greater than all the bicycles you have in the early morning, α + β. In this case, the cost is first -hα plus the Missed Costumer cost, where the unit cost of the missed customer is equal to p.

The right side of the above equation needs to be explained. The term p is simply the unit cost of the missing customer, then the term.

It is equal to an expected number of missed customers multiplied by p.

Hands-On Python Coding:

In the below, we wrote a function that is the generator of the Markov Reward Process Dictionary. The final output of the dictionary structure for the Markov Reward Process is as follows:

from typing import Dict, Tuple

MRP_dict: Dict[Tuple[int, int], Dict[Tuple[Tuple[int, int], float], float]] = {}

I did a little bit of explanation and annotation of the final data structure below:

from typing import Dict, Tuple
from scipy.stats import poisson

def generate_Markov_Rew_Process_Dict(user_capacity: int, user_poisson_lambda: int,
 holding_cost: int, missedcostumer_cost: int):
 """
 Generate a Markov Reward Process Dictionary based on the provided parameters.

 Args:
 user_capacity (int): The the capacity of the inventory.
 user_poisson_lambda (int): The Poisson lambda parameter.
 holding_cost (int): The unit cost of holding item in inventory overnight.
 missedcostumer_cost (int):The unit cost of missed costumer.
 Returns:
 Dict[Tuple[int, int], Dict[Tuple[Tuple[int, int], float], float]]: The Markov Reward Process Dictionary.
 """

 MRP_dict: Dict[Tuple[int, int], Dict[Tuple[Tuple[int, int], float], float]] = {}

 for alpha in range(user_capacity + 1):
 for beta in range(user_capacity + 1 - alpha):
 
 state = (alpha, beta)
 init_inv = alpha + beta
 beta1 = user_capacity - init_inv

 base_reward = -alpha * holding_cost
 
 for demand in range(init_inv + 1):
 if demand <= (init_inv - 1):
 
 # Calculate transition probability for demand
 transition_prob = poisson.pmf(demand, user_poisson_lambda)
 
 if state in MRP_dict:
 
 MRP_dict[state][((init_inv - demand, beta1), base_reward)]= transition_prob
 
 else:
 
 MRP_dict[state] = {((init_inv - demand, beta1), base_reward):transition_prob}
 
 
 else:
 # probability of not meeting the demands
 transition_prob = 1 - poisson.cdf(init_inv - 1, user_poisson_lambda)
 
 transition_prob2 = 1 - poisson.cdf(init_inv, user_poisson_lambda)
 
 
 reward = base_reward - missedcostumer_cost * ((user_poisson_lambda * transition_prob) -
 init_inv * transition_prob2)
 
 if state in MRP_dict:
 
 MRP_dict[state][((0, beta1),reward)]= transition_prob
 
 else:

 MRP_dict[state] = {((0, beta1),reward):transition_prob}

 return MRP_dict

Having the function, we can give the function's input (same as the previous article) and then get the dictionary of the Markov Reward Process.

# Example usage:
inv_capacity_val = 2
poisson_lambda_val = 2.0
holding_cost_val = 1
missedcostumer_cost_val = 10

MRP_dict = generate_Markov_Rew_Process_Dict(
 user_capacity= inv_capacity_val, 
 user_poisson_lambda = poisson_lambda_val,
 holding_cost = holding_cost_val,
 missedcostumer_cost = missedcostumer_cost_val)

We can print out this dictionary and figure out how the data has been stored in the dictionary:

for (state, value) in MRP_dict.items():
 
 print("The Current state is: {}".format(state))
 
 for (next_state,reward),trans_prob in value.items():
 
 print("The (State ,Reward): ({} , {:.2f}) occurs with Probability of: {:.2f} \
 ".format(next_state, reward, trans_prob ))

Bellman Equation:

The main idea of the Markov Reward Process is to figure out the expected total return of each state if we continue the process for a long time under a specific policy. The “State Value Function” that maps “Expected Return of Each State” to “State” called as “State Value Function” can be defined as:

Some explanation of the second equation is needed. The V(s) is the expected total return of following specific policy from state s, compromised of two parts. The first part is the reward we expect to get right away (immediate), plus the average value of all the different states we could go to next, times the value of those new states V(S’).

In other words, this equation is recursive.

The goal of the rest of this blog is to find the state value function V(s), which consists of two parts:

– Part I) Find the Expected Immediate Reward for all states

– Part II) Build the Transition Probability Matrix

Part I) Find the Expected Immediate Reward

The below function will find theR(s) for all the states. In fact, R(s) is the expected immediate reward for states in the inventory problem.

def calculate_expected_immediate_rewards(MarkovRewProcessDict):
 """
 Calculate the expected immediate rewards for each state in a Markov Reward Process.

 Args:
 MarkovRewProcessDict (dict): Markov Reward Process Dictionary.

 Returns:
 dict: Dictionary with states as keys and their expected immediate rewards as values.
 """
 E_immediate_R = {} # Initialize a dictionary to store expected immediate rewards

 for from_state, value in MarkovRewProcessDict.items():
 # Calculate the expected immediate reward for the current state
 expected_reward = sum(reward[1] * prob for (reward, prob) in value.items())
 E_immediate_R[from_state] = expected_reward

 return E_immediate_R

# Example usage:
# E_immediate_R = calculate_expected_immediate_rewards(MarkovRewProcessDict)

Calling the function:

R_exp_imm =calculate_expected_immediate_rewards(MRP_dict)
R_exp_imm

Part II) Build the Transition Probability Matrix

The transition probability matrix is like a table where the *states* are the column names and rows, and each cell shows the likelihood of moving from one state to another.

We can initialize this matrix with:

states = list(MRP_dict.keys())

df_trans_prob = pd.DataFrame(0.0, columns=states, index=states)
df_trans_prob

The above is the initialization of the matrix. Now we can go and start filling out this matrix as below:

import numpy as np
import pandas as pd

def create_transition_probability_matrix(MarkovRewProcessDict):
 """
 Create a transition probability matrix from a Markov Reward Process Dictionary.

 Args:
 MarkovRewProcessDict (dict): Markov Reward Process Dictionary.

 Returns:
 pd.DataFrame: Transition probability matrix.
 """
 states = list(MarkovRewProcessDict.keys())
 num_states = len(states)

 # Initialize an empty matrix with zeros
 trans_prob = np.zeros((num_states, num_states))
 df_trans_prob = pd.DataFrame(trans_prob, columns=states, index=states)

 for i, from_state in enumerate(states):
 for j, to_state in enumerate(states):
 for (new_state, reward) in MarkovRewProcessDict.get(from_state, {}):
 if new_state == to_state:
 probability = MarkovRewProcessDict[from_state].get((new_state, reward), 0.0)
 df_trans_prob.iloc[i, j] = probability

 return df_trans_prob

Calling the function:

df_trans_prob = create_transition_probability_matrix(MRP_dict)
df_trans_prob

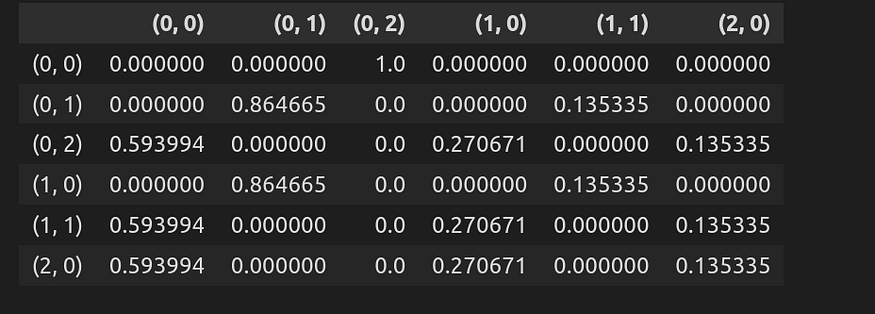
Let me explain what this matrix means. For example, think about the third row, which is state S_t=(0,2), then the following probability can be written as:

Now, having the transition matrix probability and expected immediate rewards of states, we can calculate the value function of each state using the vector and matrix format of the Bellman equation as below:

import numpy as np
import pandas as pd

def calculate_state_value_function(trans_prob_mat, expected_immediate_rew, gamma):
 """
 Calculate the state value function using transition probability matrix and expected immediate rewards.

 Args:
 trans_prob_mat (pd.DataFrame): Transition probability matrix.
 expected_immediate_rew (dict): Dictionary with states as keys and expected immediate rewards as values.
 gamma (float): Discount factor.

 Returns:
 pd.DataFrame: DataFrame with 'Expected Immediate Reward' and 'Value Function' columns indexed by states.
 """
 states = list(expected_immediate_rew.keys())

 R_exp = np.array(list(expected_immediate_rew.values()))

 # Calculate the value function vector using the equation
 val_func_vec = np.linalg.solve(np.eye(len(R_exp)) - gamma * trans_prob_mat, R_exp)

 # Create a DataFrame with 'Expected Immediate Reward' and 'Value Function' columns
 MarkRevData = pd.DataFrame({'Expected Immediate Reward': R_exp, 'Value Function': val_func_vec}, index=states)

 return MarkRevData

# Example usage:
# MarkRevData = calculate_state_value_function(df_trans_prob, E_immediate_R, gamma)

Calling this function:

calculate_state_value_function(trans_prob_mat=df_trans_prob, expected_immediate_rew=R_exp_imm, gamma=0.9)

Putting Everything Together:

One way is to put all codes together, make a MarkovRewardProcess class, and call modules of the class. I have put full code (less than 100 lines) here:

from typing import Dict, Tuple
from scipy.stats import poisson
import numpy as np
import pandas as pd

class MarkovRewardProcess:
 def __init__(self):
 self.MRP_dict = {}

 def generate_Markov_Rew_Process_Dict(self, user_capacity: int, user_poisson_lambda: int,
 holding_cost: int, missedcostumer_cost: int):
 self.MRP_dict = {} # Initialize the Markov Reward Process Dictionary

 for alpha in range(user_capacity + 1):
 for beta in range(user_capacity + 1 - alpha):
 
 state = (alpha, beta)
 init_inv = alpha + beta
 beta1 = user_capacity - init_inv

 base_reward = -alpha * holding_cost
 
 for demand in range(init_inv + 1):
 if demand <= (init_inv - 1):
 transition_prob = poisson.pmf(demand, user_poisson_lambda)
 
 if state in self.MRP_dict:
 self.MRP_dict[state][((init_inv - demand, beta1), base_reward)] = transition_prob
 else:
 self.MRP_dict[state] = {((init_inv - demand, beta1), base_reward): transition_prob}
 else:
 transition_prob = 1 - poisson.cdf(init_inv - 1, user_poisson_lambda)
 transition_prob2 = 1 - poisson.cdf(init_inv, user_poisson_lambda)
 reward = base_reward - missedcostumer_cost * ((user_poisson_lambda * transition_prob) -
 init_inv * transition_prob2)
 if state in self.MRP_dict:
 self.MRP_dict[state][((0, beta1), reward)] = transition_prob
 else:
 self.MRP_dict[state] = {((0, beta1), reward): transition_prob}

 def calculate_expected_immediate_rewards(self):
 E_immediate_R = {}
 for from_state, value in self.MRP_dict.items():
 expected_reward = sum(reward[1] * prob for (reward, prob) in value.items())
 E_immediate_R[from_state] = expected_reward
 return E_immediate_R

 def create_transition_probability_matrix(self):
 states = list(self.MRP_dict.keys())
 num_states = len(states)
 trans_prob = np.zeros((num_states, num_states))
 df_trans_prob = pd.DataFrame(trans_prob, columns=states, index=states)

 for i, from_state in enumerate(states):
 for j, to_state in enumerate(states):
 for (new_state, reward) in self.MRP_dict.get(from_state, {}):
 if new_state == to_state:
 probability = self.MRP_dict[from_state].get((new_state, reward), 0.0)
 df_trans_prob.iloc[i, j] = probability
 return df_trans_prob

 def calculate_state_value_function(self, trans_prob_mat, expected_immediate_rew, gamma):
 states = list(expected_immediate_rew.keys())
 R_exp = np.array(list(expected_immediate_rew.values()))
 val_func_vec = np.linalg.solve(np.eye(len(R_exp)) - gamma * trans_prob_mat, R_exp)
 MarkRevData = pd.DataFrame({'Expected Immediate Reward': R_exp, 'Value Function': val_func_vec}, index=states)
 return MarkRevData

mrp = MarkovRewardProcess()

# Generate the Markov Reward Process Dictionary
user_capacity = 2
user_poisson_lambda = 2
holding_cost = 1
missedcostumer_cost = 10

mrp.generate_Markov_Rew_Process_Dict(user_capacity, user_poisson_lambda, holding_cost, missedcostumer_cost)

E_immediate_R = mrp.calculate_expected_immediate_rewards()
trans_prob_mat = mrp.create_transition_probability_matrix()

gamma = 0.9 # Replace with your desired discount factor
MRP_Data = mrp.calculate_state_value_function(trans_prob_mat, E_immediate_R, gamma)

print(MRP_Data)

Key Summary:

– In this blog, the Markov Reward Process was introduced, and in the example of inventory optimization, the “reward” of the process was defined.

– A new Python data structure, “MRP_dict,” was introduced where it tracks the states, the reward, and the probability of the next (state, reward).

– The Markov Reward Process aims to find a State Value Function, meaning what the “Expected Total Return” for every state is. This was achieved by using the calculate_state_value_function in the Python code.

[1] You can read this example more in-depth in “Foundation of Reinforcement Learning with Application in Finance”. However, I have rewritten Python codes in this blog to make it easier to understand.

Thanks for reading so far!

I hope this article has provided an easy-to-understand tutorial on how to do inventory optimization with Python.

If you think this article helped you to learn more about inventory optimization and Markov Process, please give it a U+1F44F and follow!

Join thousands of data leaders on the AI newsletter. Join over 80,000 subscribers and keep up to date with the latest developments in AI. From research to projects and ideas. If you are building an AI startup, an AI-related product, or a service, we invite you to consider becoming a sponsor.

Published via Towards AI